万吨级船舶气囊下水研究成果

孙菊香 黄立身 赵光胜

（济南昌林气囊容器厂有限公司 济南250023）

引 言

2002年，满载排水量15 000 t、船体自重4 000 t、船体总长138 m的万吨级油轮“舟海油28号”在浙江台州成功使用气囊下水，不久便陆续有2万至3万吨级的各类货船采用气囊下水，并且气囊下水的船舶吨位和船舶自重不断提高。自2008年起，55 000载重吨巴拿马型船“VICTORIA Ⅰ”号在浙江三门下水，其后接连又有57 000载重吨、70 000载重吨的船舶下水，直至2012年出现82 000载重吨巴拿马型散货船“PRETTY MASTER”号在浙江庄吉船业有限公司下水，此时的下水质量已达到13 000 t。下页图1为70 000载重吨的船舶下水图。

上百艘万吨船采用气囊下水成功，气囊下水的吨位也越来越大，取得这些成果除工艺操作水平提高外，与以下各项研究成果均有密切关系。

图1 70 000载重吨的船舶下水

1 气 囊

气囊承载能力的提高是实现万吨船舶下水成功的第一关键，从受力分析和长期应用实践已证实缠绕型的结构是最优秀的，我们又从万吨船使用特点中进一步找出气囊制作中帘子布的最佳缠绕角，从而提高了气囊承载力。

万吨船用气囊下水初期大多使用直径1.5 m的气囊，起墩时充气压力达到0.13 MPa，每个长度为18 m的气囊有2 500 kN承载力。如今，最新产品的充气压力已达到0.16 MPa，长度也增至24 m，直径1.5 m的气囊在起墩时就能有4 000 kN承载力。按此推算，今后所有巴拿马船型和其他常规型的各种货船（即使载重量达到10万吨）都能用气囊下水。从目前情况看，具有最佳缠绕角的气囊是今后大型船舶气囊下水用的最佳载体。

2 坡 道

气囊在倾斜的坡道上滚动，以区别滑道滑板的下水方式，驮载船体下水，而这种用于气囊下水的带有坡度的特殊地面道路则称为“坡道”。船体建造时船台部分地面道路也应包括在坡道之内，本文只讨论坡道斜度、长度和强度。

气囊下水初期只用于内河小船，这是由于船体轻，气囊可以在泥地甚至草地上滚动。第一艘采用气囊下水的万吨船以及其后第一批1万至2万载重吨的船仍然是在泥地上下水。这些坡道由于经过长期使用，已经压得很结实，初期尚能承载1万至2万吨级的船舶下水，但在临近海水浸泡的区域就很危险，存在不安全因素，为此我们提出，今后万吨船必须建钢筋水泥混凝土下水坡道。经过多年研究，我们已为多家船厂设计了新型适用气囊下水的折角型坡道（由主坡道和副坡道两部分构成）参见图2。

图2 气囊下水用的折角型坡道

船体就在主坡道上建造，其长度应达到施工要求。主坡道的坡度K1应达到船体在解脱牵引后能自滑，但也没有必要取过大的坡度，因为坡度加大，牵引力就要求更大，容易发生事故，且船台建造投资也更加大。

关于K1的选取：由于船体自滑力是自重的分力，所以自重越大、自滑力也越大。与传统滑道设计相同，下水船舶自重越大，坡道的坡度应相对较小。因此，根据近年来万吨级船使用情况，提出以下意见（见表1），仅供参考。

表1 主坡道坡度

主坡道的坡度确定最后还需要综合考虑原始场地的地形、地貌对施工条件和投资成本的影响，以及地质、水文、气象条件等诸多因素，表1仅考虑船舶质量大小引起的对牵引力的要求。

副坡道的长度要求在其上能放置5个气囊，起到相应的承压作用就行，所以使用直径为1.5 m气囊时，副坡道长度一般取13～15 m，过长就不起作用。

副坡道的坡度K2不能太大，否则第5个气囊就不能起到有效作用（不受压缩），若用直径为1.5 m的气囊，坡度1/10 以后就会出现这种情况。该坡度K2也不能太小，如果小于船体倾斜后的最大倾斜度，就会出现副坡道上最靠尾部的一个气囊压缩量大于拐点上气囊的压缩量，这样不仅气囊有危险性，还对坡道末端造成很大压力，容易发生事故。根据近年来的3万至8万载重吨尾机舱货船下水计算，一般当水位到达拐点时，船体最大倾斜度1/32～1/28，所以坡度应大于1/28为宜。目前使用直径1.5 m气囊时，一般多数取K2=1/15～1/25。

副坡道及主坡道后半部必须用钢筋水泥混凝土建造并有足够的强度。

3 牵引力计算

气囊下水技术推广最初10年间，由牵引失败而造成的事故占气囊下水事故之首，而且其危害性大，随着万吨级船舶自重增加，牵引力的要求就更大，所以更应重视牵引力的计算。牵引力F推荐按下式计算：

式中：F为牵引力/kN；W为船舶自重/kN；α为船舶龙骨倾角/（º）；μ为气囊滚动阻力系数；k1为安全系数（k1=1.5～2.0），目前多数取2；k2为船舶气囊下水工艺操作影响系数，与气囊充气压力、摆放平行度等有关。

上式中的气囊滚动阻力系数至今尚无准确的计算方法。在小型船计算时，从安全角度考虑，可以不计算此值，但若大型船也如此做则会造成误差太大。为解决这一难题，故对多艘万吨船在不同坡度的坡道上下水时是否能自滑进行观察（即下达下水指令脱开牵引后船舶能否自行下滑）。若能自滑，此坡道的坡度值必定大于气囊滚动阻力系数。当观察多艘7.0万吨和5.7万吨等巴拿马型船在主坡道1.2/100～1.25/100的坡道上下水时发现，其中的多数均不能自滑，但这些船在坡度1.3/100坡道上下水时则全部能自滑，由此得知气囊滚动阻力系数μ<1.2/100（因为只要有一次能自滑，就说明这一点，其他不能自滑者，主要是气囊在铺放过程中的不平行度造成）。

尽管工艺要求气囊铺放与船体中心线垂直，要求全部呈平行状态，可是气囊是柔软的长条,实际操作时很难使数十个气囊都达到平行，必定会有误差，所以就出现姊妹船在同一条1.2/100坡道上下水时不自滑的情况，这种因素被称为操作影响系数k2。若将k2μ结合在一起，其值开始接近而小于1.2/100。为了安全以及其他未知因素，推荐k2μ= 0.006 5～0.008 5，供计算参考应用（适用主要气囊内压0.13～0.16 MPa）。经过我们在多艘船计算中应用，按公式计算得到的牵引力是目前常用牵引设备所能实现且有安全保证。

上述参考值只供下水时应用，因为上水作业（指船舶从水中拉上岸坡）摆放气囊更困难，很多作业在水中又与船牵引前进同时进行，气囊的不平行度更大，所以上述推荐值不能应用于气囊上水作业中。

4 下水计算

气囊下水工艺始于1981年，直到2002年万吨船开始应用后，一直没有下水计算方法。经过多年试算、反复修改，终于用静力平衡的原理与逐步近似的计算方法研发出一套气囊下水计算方法［1，2］。

按下水过程船体承载不同，可分为三个阶段：

（1）船体全部由气囊承载。

（2）船体由气囊和水浮力共同承载。

（3）船体全部由水浮力承载，这就是船舶静力学中的全浮状态。

计算方法全部按船舶静力学方法进行，以下只介绍第1阶段和第2阶段的计算方法。

任何阶段任何时刻都必须达到静力平衡，满足以下两式：

表2 起墩时气囊承载力计算（D =1.5 m）

表3 船体重心到达拐点时气囊承压力计算

表4 船体浮力计算

下水计算长期不能实现，其中有一个最关键的气囊刚度没有求出，因为起墩结束，船体自滑开始后，气囊相对地面的位移速度仅为船体移动速度之半，造成艉部悬空长度随着船体前移越来越长，艉部从一开始就产生一个微小的艉倾角并逐步加大，在此运动过程中，每个气囊的工作高度和内压都在变化，所以必须先求取气囊的刚度。我公司在通过三次压缩性能试验并与浙江工业大学合作在一些实船上经过压力测试后，提出气囊内压随工作高度变化的计算方法：

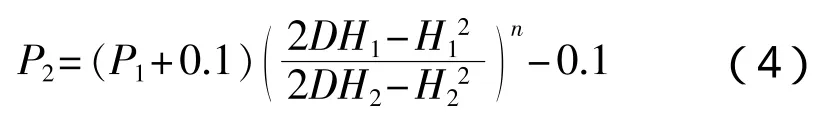
式中：P1和H1分别为气囊初始时（即起墩时设置的工作压力和工作高度，见表2的数据）对应的工作压力和工作高度；P2和H2分别为计算行程点气囊瞬时工作压力和工作高度（计算按表3进行）。D为气囊直径，m。

n=1.1～1.2。当起始工作压力越高，取大值；如达到＞0.13 MPa时，取1.2；当起始压力在0.10～0.13 MPa时，可取1.15；当起始压力＜0.10 MPa时，可取1.1。

我们所做的压缩试验最大气囊变形率仅70%，大于70%后的误差较大。

以下分别取第1阶段和第2阶段中最典型的最重要位置作些说明。

4.1 起墩计算

起墩计算属第1阶段，没有水浮力，凡第1阶段任何时刻都可参照表2格式计算。

起墩计算是气囊下水中一道重要工序，即先抬起原来坐落在硬墩上的船体，撤掉墩木后再转换到气囊上的全过程。所有气囊承载力要全部托起船体质量，其平衡条件可简化为：

见过表2就能了解每个气囊承载力及其对重心之矩的计算方法和结果。计算过程必须通过多次调节气囊内压值、数量、型号、间距等逐步满足式（5）和式（6）的要求。

4.2 船舶重心到达坡道拐点时的计算

绝大多数常规船其重心到达折角型坡道拐点时，处于拐点附近的气囊其内压和船舶内应力都处于最高位，这时候船体受气囊和水浮力共同承载，属第2阶段计算，凡第2阶段都可以用此方法计算。进入第2阶段，气囊在船下的数量越来越少，船移到新位置后，其数量和位置可根椐“气囊前移速度是船体移动速度之半”的关系确定，参照表3格式便可计算出这部分气囊的承载力。先假定船体倾斜度和拐点上的气囊（如表3中的13号气囊）的工作高度H13能完成表3的全部计算，然后把相同的倾斜度和工作高度H13代入表4，借助邦氏计算表就能算出水浮力和浮力对舯之矩（这个对舯之矩必须换算出对重心之矩）。为缩短反复计算的次数，首次取倾斜度和H13应参考近似船舶的数椐，倾斜度也可取在主坡度与副坡度之间，一般巴拿马型船可取0.025～0.035之间。

由表4最后一行数据得：

浮力=1.025×10.925×232.16×9.81 =25 503.61 kN（10.925 m为站距=L/20，L= 218.5 m为两柱间长）浮心距舯=10.925×（-1 165.91）/232.16=-54.86 m重心距舯=L/2-LCG=8.95 m（LCG为重心距尾柱的距离）

将表3和表4的计算结果同时代入下页表5，要求满足式（2）和式（3）的要求，否则要重新假设倾斜度和工作高度H13，直到满足为止。一般都要经过很多次计算才能近似满足，所以这是一个逐步近似的过程，可用本原理编制程序计算后就能达到高效率。

表5 综合计算

4.3 下水最低水位确定和气囊强度的校核

计算后可获得船底高度以及每一个气囊新的内压值，一般对常规万吨级船当船舶重心到达折角型坡道拐角点上就出现气囊的工作高度最低，而内压最高（也可以增加其他位置，用同样方法计算与其比较，查找有否更高的内压值）。只要气囊的最高工作压力不超过该气囊的使用压力（由气囊生产厂方提供），应视为安全，这也说明该计算水位是允许的，否则应调节气囊布置方案，如增加气囊、减少气囊间距、更换气囊型号等，如果最终还达不到要求，就应认为该计算水位不适合下水，建议等待水位增加后再下水。

计算后知气囊受压最重处及其起始位置，应当把最优质气囊放于该起始位置。

5 结 论

如今，船舶使用气囊下水已由初期只能下水几十吨内河小船发展到目前大量万吨级船舶（最大自重已达13 000余吨）的安全下水，这主要依托于气囊承载力的提高以及新型的下水坡道型式和不断进步的气囊下水计算方法。气囊下水计算方法能在下水前科学地计算出下水全过程中气囊的位移、压力和工作高度，以及相互关系等诸多动态技术参数，因而能对下水安全作出更准确的预报与评估，使气囊下水工艺在理论上达到新的水平。只要采用这种计算方法，并严格按操作规程（参阅国际标准：船舶与海事技术——船舶用气囊下水方法学）进行，10万载重吨以内的常规型船舶都能安全下水。

［1］ 朱珉虎，孙菊香.船舶气囊纵向下水计算方法的研究［J］.船舶，2009（3）：39-44.

［2］ 孙菊香，徐才中，黄立身.70 000吨级船舶气囊下水的计算与实践［J］.造船技术：2011（3）.42-45.

［3］ 浙江工业大学.关于气囊刚度的研究报告［R］.2007.6.

［4］ 孙菊香，朱珉虎.走出一条船舶柔性下水的新路［J］.船舶，2013（5）：81-84.