碎纸片的拼接复原
刘啸泽,李 璞,陈 香
(西安电子科技大学,陕西西安,710126)
1 问题重述
破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用.传统上,拼接复原工作需由人工完成,准确率较高,但效率很低.特别是当碎片数量巨大,人工拼接很难在短时间内完成任务.随着计算机技术的发展,我们尝试使用碎纸片的自动拼接技术,以提高拼接复原效率.
2 符号说明
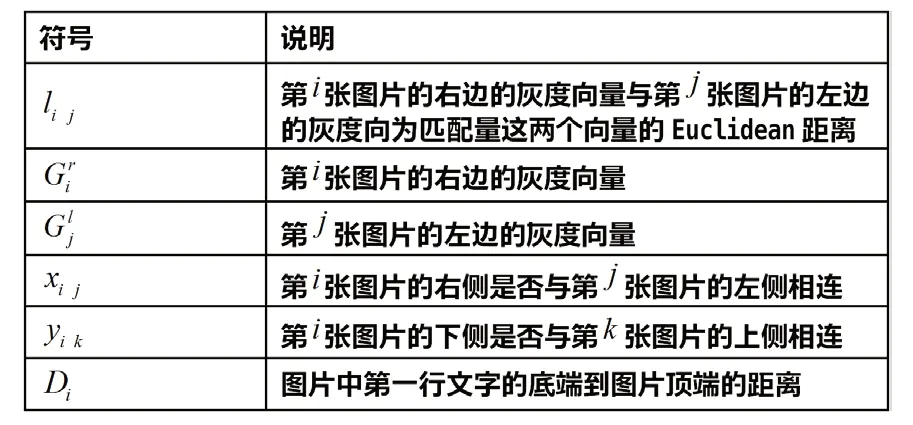
3 问题一的求解
3.1 模型I —— 贪心算法的设计
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择.也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解.贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解.
对于一个给定的问题,往往可能有好几种量度标准.初看起来,这些量度标准似乎都是可取的,但实际上,用其中的大多数量度标准作贪婪处理所得到该量度意义下的最优解并不是问题的最优解,而是次优解.因此,选择能产生问题最优解的最优量度标准是使用贪婪算法的核心.
一般情况下,要选出最优量度标准并不是一件容易的事,但对某问题能选择出最优量度标准后,用贪婪算法求解则特别有效.最优解可以通过一系列局部最优的选择即贪婪选择来达到,根据当前状态做出在当前看来是最好的选择,即局部最优解选择,然后再去解做出这个选择后产生的相应的子问题.每做一次贪婪选择就将所求问题简化为一个规模更小的子问题,最终可得到问题的一个整体最优解.
首先本文为了使求解过程不致过于复杂,故只为图片去拼其右边,所以在拼接时只用考虑为已知图片去拼接其右边即可.而贪心算法最为关键的是选出最优度衡量标准,本文选取已知图片的右边界的灰度向量与待匹配的图片的左边界的灰度向量的Euclidean 距离最小作为最优度衡量的指标(如式(5)所示).并且本文所研究的问题比较特殊,这些图片的拼接具有唯一性,所以每一步的最优解最终必会导致全局最优解,从而也避免了陷入局部最优解这个陷阱.
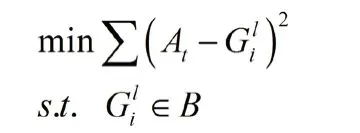
(式中 为已确定选取的图片的右边界的灰度向量, 为第 i 张图片的左边界的灰度向量)
Step 1.首先将每张图片的左侧向内延伸若干个像素点,在这个矩阵内的灰度值均为255,即均为白色,则可以断定其为这张完整的纸的位于最左侧的子图片,将其放置于 中的 ,作为以确定选取的图片;
Step 2.将已入 之外的其他图片剪切至待拼的左侧向量库B 中;
Step 3.根据上述选择的最优度的衡量指标选择出与 拼接的最优的匹配向量,从而确定出与 拼接的最优的图片;
Step 4.判断待拼的左侧向量库B 中所余向量个数是否大于1,若大于1 表明待拼接图片尚存,转入step 2,否则结束.
3.2 模型II —— 基于TSP 问题的0-1 整数规划模型
针对问题一,主要就是做文字的拼接,而能拼接到一起的两张图片在边沿非常小的一段内具有很强的相似性,本文采用每张图的灰度值矩阵的最左与最右的两个列向量作为这张图的特征值,然后用一张图的最右的这个列向量去和其他图的最左的列向量进行匹配,通过这两个向量的Euclidean 距离。
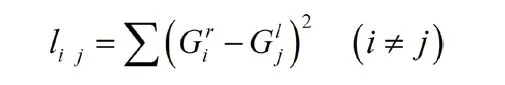
(式中 表示的是第i 张图片的右边的灰度向量与第j 张图片的左边的灰度向量之间的Euclidean 距离, 表示第i 张图片的右边的灰度向量, 表示第j 张图片的左边的灰度向量)来作为评价指标,两张图的边界的灰度向量的Euclidean 距离越小,其匹配程度越好.整张图的拼接匹配的目标为拼接出来的图的边界灰度向量的Euclidean 距离之和最小.而一张完整的纸的两端均是全白色,故两端可拼接到一起.因为每张图的右侧只可能紧密连接一张图,并且每张图只用一次,故可以将这个问题抽象为一个TSP 问题进行求解.
即我们可以把每一张碎纸片类比成为一个城市。而把两张图片之间的Euclidean 距离类比为两个城市之间的距离。从而将碎纸片的拼接和TSP 求解联系起来。
TSP 问 题(Travelling Salesman Problem),即 旅 行 商 问题.假设有一个旅行商人要拜访n 个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市.路径的选择目标是要求得的路径路程为所有路径之中的最小值.
为了求解这个TSP 问题,建立以第j 张图片的右边是否与第 张图片的左边相连为决策变量,以所有相连接的图片的右边的灰度向量与图片的左边的灰度向量这两个向量的距离之和最小为目标函数,建立一个0-1 整数规划模型,其约束条件具体如下:
1)每张图片的右边只有一张图片与之相连;
2)每张图片的左边只有一张图片与之相连.
运用LINGO 求解上述0-1 整数规划模型,结果会呈现为一个封闭的圆环,出现这种情况的原因是因为在一整页纸的首尾都是空白的,其两张图片的边缘的灰度向量之间的距离会非常小,故会连接成一个圆环.所以需确定页面从哪里切开.通过MATLAB将每张图片的左侧向内延伸若干个像素点,在这个矩阵内的灰度值均为255,即均为白色,则可以断定其为这张完整的纸的位于最左侧的子图片.所以将该圆环从这张图片的左侧切开即可.
4 问题二的求解
4.1 多目标的0-1 整数规划模型
问题二是问题一进行了复杂化,每张图片变小了,从而边缘的信息量也变少了,而且每张图片不仅需要考虑左右拼接,还需要考虑上下拼接.为了使问题的求解简化,可以只考虑每张图用其灰度值矩阵的最左和最下去和其他图片的最右和最上的向量进行匹配,通过这两组向量的Euclidean 距离之和最小来衡量其匹配程度.
但是考虑到在这一问中图片变小了,导致边缘的信息量也随之变小,所以再确定一个目标——最上面一行字到该图片上沿的距离 尽可能的相同,从而可以建立一个多目标的0-1 整数规划模型.
本文建立以第i 张图片的右边是否与第j 张图片的左边相连,第i张图片的下边是否与第k张图片的上边相连为决策变量,以相接处的两组灰度值矩阵的边界向量的Euclidean 距离之和最小,处于同一行的图片的特征值之差的绝对值的最大值最小为目标函数,建立一个多目标的0-1 整数规划模型,其约束条件具体如下:
1)每张图片的右边只有一张图片与之相连;
2)每张图片的左边只有一张图片与之相连;
3)每张图片的上边只有一张图片与之相连;
4)每张图片的下边只有一张图片与之相连.
具体模型如式(6)所示:


这是一个多目标的0-1 整数规划问题,对于最优解的求取存在一定难度,并且过程会比较复杂.所以为了求解这个问题,需要将其转化为单目标问题,故选择特征值 作为指标来进行聚类,这样在同一类内就转化为了单目标的整数规划问题.
4.2 图片的聚类
为了优化上述的多目标的0-1 整数规划模型,从其第二目标引入的原因入手.由于元素即子图片过多,从而仅用一个指标来评价匹配的程度使得误匹配率上升,所以可以采用聚类的思想,使得待匹配的子集尽量的小,从而使问题较准确地求解.
考虑到汉字大部分都是比较规整的占据一个比较方正的空间,并且在打印中,行距为固定的,一行字的高也是固定的,如图3 所示,即d、D 是固定的,所以对于汉字本文选取作为该图片的特征值,依此作为汉字的聚类标准.
对于英文单词,由于有些小写字母并不规整,所以英文的聚类标准并不能用汉字的聚类标准.考虑到比较特殊的字符有g、j、p、q、y 这五个,分析所有图片,可以将每张图片的灰度值矩阵从左向右求和,从而做出其投影(如图4 所示),而行线应画在其投影的斜率较大的地方.行线的确定如图4 所示.
根据每张图片最左边的白色区域最早结束的距离可以寻找出这11 行的行首,然后对剩下的每张图片计算其各自的,根据其数值进行聚类,具体步骤如下:
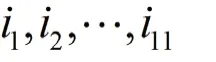
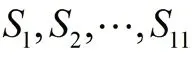
4.3 每一类内的拼接
根据聚类结果,在每一类内包含有19 张图片,且这一类中为完整图片的一行内,所以可以利用问题一中的模型进行对其进行拼接.
对11 行分别利用问题一中的0-1 整数规划模型进行求解,代入数据,利用LINGO 求解之,再利用问题一中相同的方法,将所得的一个封闭圆环,进行分割,从而拼出11 个横条出来.
而在拼接英文有一行非常特殊,在这行靠右的部分其上部是一句话的结尾,并且英文单词之间的距离比较大,尤其是一句话结束的部分其间隔比较大,这样匹配会出现很多误匹配,尤其是边沿信息量非常小甚至没有的片段,所以在这里需要人工介入,根据计算机拼接出来的三段,进行人工拼接。
[1] 卓金武,MATLAB 在数学建模中的应用,北京航空航天大学出版社,2011.4;
[2] 张志涌,精通MATLAB R2011a,北京航空航天大学出版社,2011.

