一个本原有向图的scrambling指数和广义scrambling指数

樊 瑞，高玉斌

(中北大学数学系，山西太原030051)

1 预备知识

近年来，scrambling指数和广义scrambling指数是本原有向图的一个新兴研究分支.scrambling指数的研究是基于矩阵(或有向图)的本原性特征，它在经济学、生物学、化学、计算机科学等众多学科中都具有广泛的应用和重要的研究意义.2009年，Mahmud Akelbek和Steve Kirkland在文献[1]中给出了有关本原有向图scrambling指数的定义，并且讨论了一类最小圈长为s的n阶本原有向图的指数的上界.同年，两位作者又在文献[2]中对达到scrambling指数的上界K(n，s)的图进行了刻画，求得了所有达到上界的本原有向图.2010年，陈佘喜和柳伯濂在文献[3]中研究了对称图scrambling指数的指数集、上界和极图.随后，柳伯濂和黄宇飞在文献[4]中研究了含d个环的本原图，极小强连通图，几乎可分解图以及极小对称图等本原图的scrambling指数，之后，两位作者又在文献[5]中给出了广义scrambling指数的定义，并且研究了几大类图的广义scrambling指数.

定义1.1[1]设D是n阶本原有向图，若存在正整数k，对于D中任意顶点vi和vj，都存在点ω∈V(D)，使得从vi和vj到ω都有k长途径，满足上述条件的最小正整数k称为本原有向图D的scrambling指数，记作k(D).

定义1.2[5]设D为n阶本原有向图，λ，μ∈Z，1≤λ，μ≤n.对于集合+X⊆V(D)定义(D)为最小的正整数l，使得存在μ个顶点ω1，ω2，…，ωμ∈V(D)，对任意的x∈X，都有，则

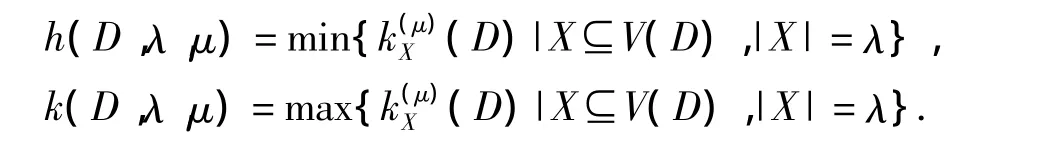
分别称为本原有向图D的λ重下μ－scrambling指数和λ重上μscrambling指数.特别地，当μ=1时，h(D，λ)=h(D，λ，1)，k(D，λ)=k(D，λ，1)，kX(D)=(D).

定义1.3[5]设D为n阶本原有向图，l为非负整数，当X⊆V(D)，且X≠∅时，(X)表示从集合X中的点出发，经过l长途径所能到达的点的集合.特别地，当l=0时(X)=X.

图1 本原有向图

2 主要结果

本文主要研究一个本原有向图D(图1)的scrambling指数和广义scrambling指数，其中含有一个n(n≥7且n=2s－1)圈和两个s圈.

定理2.1 设D是n(n≥7且n=2s－1)阶本原有向图(图1)，则有

证明 因为D含有一个n(n≥7且n=2s－1)圈和两个s圈，由本原有向图scrambling指数的定义可知，下面只需证明对于任意顶点u，v∈V(D)，都有({u})∩({v})≠∅成立，并且存在顶点 vi，vj∈V(D)，使得({vi})∩({vj－1})≠∅.

由上可知，k(D)=l.

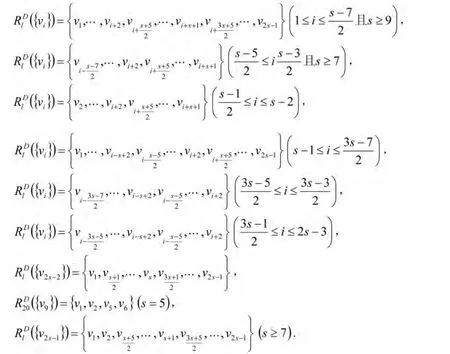
由上可知，k(D)=l.

定理2.2 设D是n(n≥7且n=2s－1)阶本原有向图(图1)，则

一方面，存在顶点v2∈V(DT)，使得

所以，对于任意顶点 vi∈V(DT)(i=1，2，…，2s－1)，都有＜λ成立.

定理2.3 设D是n(n≥7且n=2s－1)阶本原有向图(图1)，则

证明 设u1，u2，…，um(1≤m≤s)是本原有向图D(图1)中s圈上的任意m个不相同的点，并且，记长为s 的圈为Cs.首先证明 k{u1，u2，…，um}(D)≤s.考虑有向图 D(s)，显然 u1，u2，…，um是有向图 D(s)上的环点，故因此，，其中 i=1，2，…，m.

(D(s))，使得i=1，2，…，m.也就是说，图D中存在一个顶点 w∈V(D)，使得i=1，2，…，m.由此可知，k{u1，u2，…，um}(D)≤s

另外，对于任意λ个顶点vi∈V(D)，存在顶点wi∈V(Cs)，使得如果 λ ≤s，则|{w1，w2，…，wλ}|≤λ ;如果 λ ＞ s，则|{w1，w2，…，wλ}|≤s.可推出

[1]Akelbek M，Kirkland S.Coefficients of ergodicity and the scrambling index[J].Linear Algebra and its Applications，2009，430:1111－1130.

[2]Akelbek M，Kirkland S.Primitive digraphs with the largest scrambling index[J].Linear Algebra and its Applications，2009，430:1099－1110.

[3]Chen S，Liu B.The scrambling index of symmetric primitive matrices[J].Linear Algebra and its Applications，2010，433:1110－1126.

[4]Liu B，Huang Y.The scrambling index of primitive digraphs[J].Computers and Mathematics with Applications，2010，60:706－721.

[5]Huang Y，Liu B.Generalized scrambling indices of a primitive digraph[J].Linear Algebra and its Applications，2010，433:1798－1808.