水二聚体间电荷转移与分子轨道研究

潘 章

（唐山学院 教务处，河北 唐山063000）

0 引言

液态水体系是典型的氢键体系，一般认为氢键能量中包含静电能（electrostatic，ES）、电子极化能（polarization，PL）、交换互斥能（exchange repulsion，EX）、电荷转移能（charge transfer，CT）和耦合作用能（coupling，MIX）等，其中的电荷转移是指氢键供体－受体间的电荷转移，这是一种典型的量子效应，无法用经典力学方法准确地描述。因此，对常温下液态水体系的模拟研究采用从头分子动力学方法更加合适［1－2］。基于密度泛函理论的从头分子动力学方法（car－parrinello ab initio molecular dynamics，CPMD）早在20世纪90年代就被用于研究液态水体系，此后应用CPMD方法的研究工作被相继报道［3－4］。目前的研究表明，用色散修正后的BLYP（Becke－Lee－Yang－Parr）交换关联函数进行 CPMD 模拟，得到的模拟结果与实验结果符合性很好［5－6］。另据研究表明氢键能量强烈依赖于距离和角度［7］，因此水二聚体间构型发生变化必然会影响二聚体分子间的电荷分布。本文系统地研究了水二聚体在不同构象时的原子电荷分布以及分子轨道的变化情况，以便使水中氢键的本质特点表现得更加清晰。

1 模拟参数与计算细节

CPMD方法是在赝势和平面波的基础上具体实现的［3，8］，本文应用CPMD方法结合限定性动力学方法对水二聚体进行模拟。设定立方体盒子的边长为L＝18.897 3a.u.。模拟采用BLYP的交换关联泛函和范数不变的Troullier Martins赝势近似。Kohn－Sham轨道在平面波基组下展开，能量截断为70Ry，虚拟电子质量为600a.u.，时间步长设置为5a.u.（0.121fs），温度为330（±20）K。模拟过程中限定了二聚体O－O间的距离R和角度θ。几何参数和坐标系参见图1，图1中y轴是氢键受体分子的角∠HOH的平分线，z轴与氢键受体分子所在平面垂直，z轴与连线O…H的夹角定义为角Ψ。绕x轴、y轴、z轴旋转的角度分别定义为Ψx，Ψy和Ψz。优化后的水二聚体几何参数为RO…O＝2.97A，rO…H＝1.99A，Ψ＝32°以及θ＝169.42°。为了系统计算水二聚体在不同构象下的电荷分布及分子轨道，通过限定性动力学方法将距离r和角度θ限定在上述值。动力学模拟之前计算了孤立水分子的原子电荷分布（见表1）及经过优化的二聚体的分子轨道（见图2），并与文献中报道的相关计算结果进行了对比［9－11］，证实了选用参数的可靠性。

表1 孤立水分子原子电荷分布

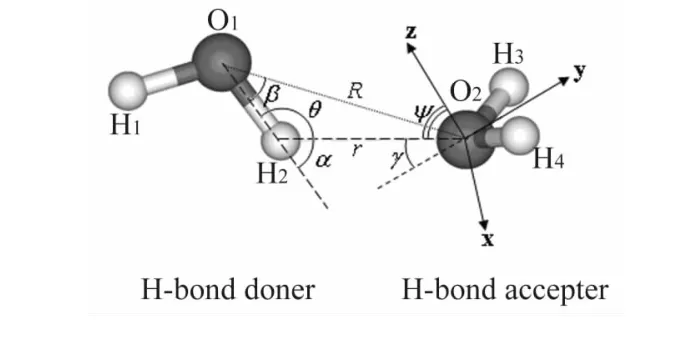
图1 优化后水二聚体及相关的距离和角度

图2 通过CPMD方法计算得出的孤立水分子5个占据轨道［10－11］

2 水二聚体不同距离的原子电荷分布

氢键的能量受电荷转移的影响，且强烈地取决于水二聚体间的分子取向，因此分子间距离的变化必然影响水分子间的电荷转移。根据自然键轨道理论（natural bond orbital，NBO）分析，电子转移是指电子从水二聚体的受体水分子转移到供体水分子上。为了研究电荷转移与水二聚体氧氧间距离的关系，我们只改变氧氧间的距离，其他取向保持与优化后的结果相同，计算不同氧氧间距离时水分子的电荷分布情况，计算结果见表2和图3。表2中供体水分子的净电荷是负值，即q（donor）＝q（O1）＋q（H1）＋q（H2），受体水分子的净电荷是正值，即q（accepter）＝q（O2）＋q（H3）＋q（H4），从表中很容易看出它们的绝对值是相等的。从图3可以明显看出随着氧氧间距离的增加，电荷转移的程度在降低。通过数据拟合的方法可以得出电荷转移程度与氧氧间距离的函数关系大约为CT＝0.94×e－R。从图3可以看出当氧氧间距离大于5A时，电荷转移已经非常弱了。

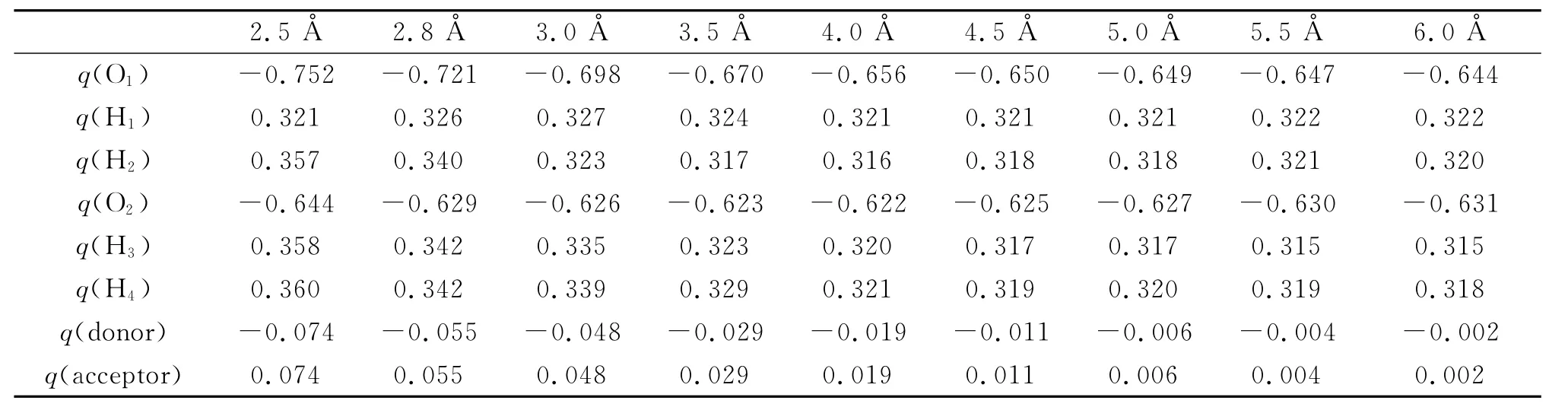
表2 原子电荷随氧氧间距离的分布

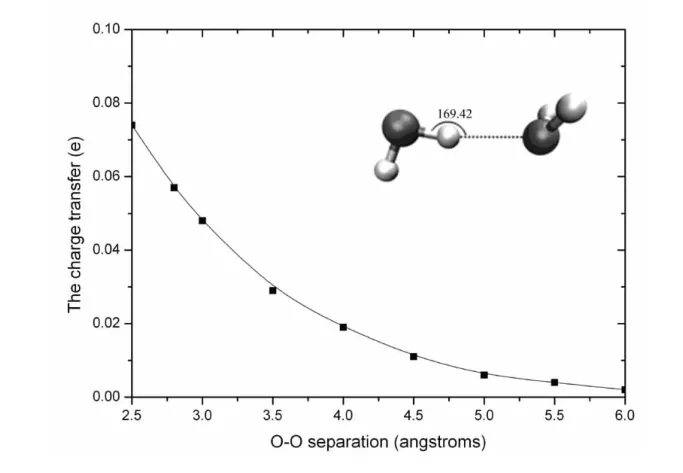
图3 电荷转移程度随氧氧间距离R的变化曲线

3 水二聚体分子轨道随氧氧间距离R的变化关系

分子轨道可以使电荷转移的程度可视化，并且可以更加形象地了解分子间相互作用的关系，因此分子轨道是研究电荷转移的有效方法。水二聚体间的分子轨道是孤立水分子占据轨道的线性组合，图4中给出了4组水二聚体间的分子轨道，其含义分别是：（b2／a1）分子轨道表示氢键受体水分子的3a1轨道与供体水分子的1b2轨道组合，其中1b2占主要部分，3a1占次要部分；（b2／a1）＊轨道是（b2／a1）的反键轨道，与（b2／a1）分子轨道不同的是3a1占主要部分，1b2占次要部分。类似地，分子轨道（a1／b1）和（a1／b1）＊均是由氢键受体水分子的3a1轨道与供体水分子的1b1轨道线性组合，（a1／b1）轨道中3a1轨道占主要部分，1b1占次要部分，而（a1／b1）＊轨道中1b1轨道占主要部分，3a1占次要部分。本文计算了上述4组分子轨道随氧氧间距离的变化情况。从图4可以看出随着氧氧间距离的增大，分子轨道间的重合程度显著降低，当氧氧间距离大于5A时，水二聚体间的分子轨道已经接近于孤立水分子的分子轨道，例如，图4（a）的最后一个分子轨道已经与孤立水分子的1b2轨道接近，图4（b）的最后一个分子轨道已经与孤立水分子的3a1轨道接近，图4（c）、图4（d）也表现出了相同的结果，即氧氧间距离大于5A时供体与受体水分子间分子轨道的线性组合已经基本消失，电荷转移的影响已经非常微弱，这与上面计算的电荷分布情况一致。

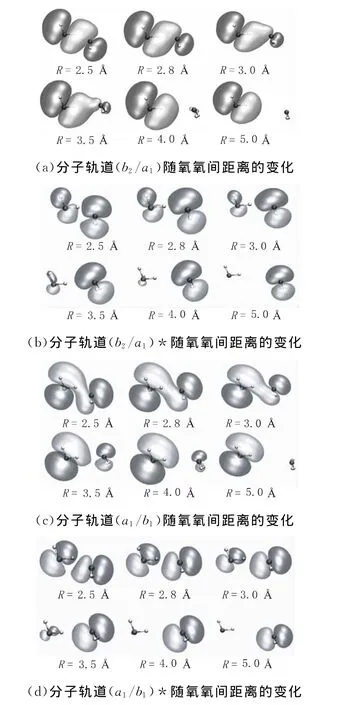
图4 水二聚体4组分子轨道随氧氧间距离的变化

4 结论

电荷转移在氢键的形成中占有重要的作用，本文应用CPMD方法并结合限定性动力学方法系统计算了水二聚体电荷分布及分子轨道随氧氧间距离的变化，计算结果可以清楚地表明电荷转移程度随着距离的增加而减弱，当氧氧间的距离R≥5A时，电荷转移程度已经非常微弱，电荷转移随氧氧间距离R的函数关系近似为CT＝0.94×e－R。分子轨道分析清晰地反映了电荷转移的过程，这对于分析电荷转移的本质有着重要的帮助。

［1］ Morokuma K.Why do molecules interact？the origin of electron donor－acceptor complexes，hydrogen bonding and proton affinity［J］.Acc.Chem.Res，1977，10（8）：294－300.

［2］ Steiner T.Hydrogen bond in solid state［J］.Angewandte Chemie International Edition，2002，41（1）：48－76.

［3］ Car R，Parrinello M.Unified approach for molecular dynamics and theory［J］.Phys Rev Lett，1985，55（22）：2471－2474.

［4］ Tuckerman M E，Parrinello M.Integrating the Car－Parrinello equations.I.Basic integration techniques［J］.J Chem Phys，1994，101（2）：1302－1315.

［5］ Grimme S.Density functional theory with London dispersion corrections［J］.WIREs Comput Mol Sci，2011，1（2）：211－228.

［6］ Zimmerli U，Parrinello M，Koumoutsakos P.Dispersion corrections to density functionals for water aromatic interactions［J］.J Chem Phys，2004，120（6）：2693－2699.

［7］ Kumar R，Schmidt J R，Skinner L.Hydrogen bonding definitions and dynamics in liquid water［J］.J Chem Phys，2007，126（204107）：1－12.

［8］ Lee H S，Tuckerman M E.Structure of liquid water at ambient temperature from ab initio molecular dynamics performed in the complete basis set limit［J］.J.Chem.Phys，2006，125（154507）：1－14.

［9］ Martin F，Zipse H.Charge distribution in the water molecule－a comparison of methods［J］.J.Comput.Chem，2005，26（1）：97－105.

［10］ Tachikawa H.Electron capture dynamics of the water dimer：a direct ab initio dynamics study［J］.Chem.Phys.Lett，2003，370（1）：188－196.

［11］ Pieniazek P A，VandeVondele J，Jungwirth P，et al.Electronic structure of the water dimer cation［J］.J.Phys.Chem.A，2008，112（27）：6159－6170.