两边空间分数阶反常扩散方程的一种有限差分解法

马亮亮，刘冬兵

（攀枝花学院 数学与计算机学院，四川 攀枝花617000）

0 引言

反常扩散现象在自然科学和社会科学中大量存在，如污染物在土壤中的迁移、石油渗流、地下水传输、湍流等［1－2］，这些扩散现象由于不满足经典的Fick梯度扩散率，因而被称为反常扩散［3－5］。

反常扩散过程本质上是时间上有记忆性和空间非局限性的过程，与整数阶导数定义相比，分数阶反常扩散方程能够更准确地描述反常扩散过程［5－17］。因此，对分数阶反常扩散方程进行数值求解有着十分重要的意义。

本文考虑如下两边空间分数阶反常扩散方程的混合问题：

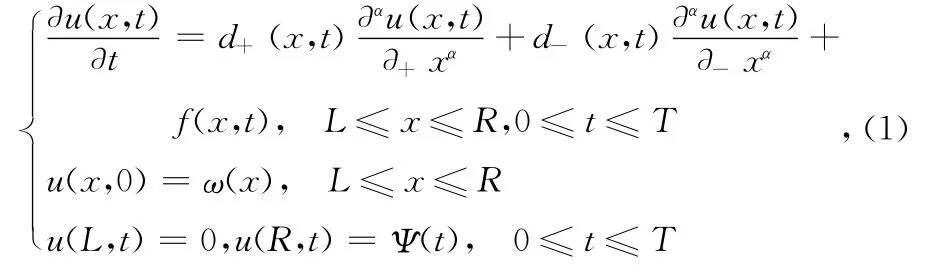
其中1＜α≤2，d＋（x，t）和d－（x，t）是非负的有界函数，为 Riemann－Liouville分数阶导数［18］：

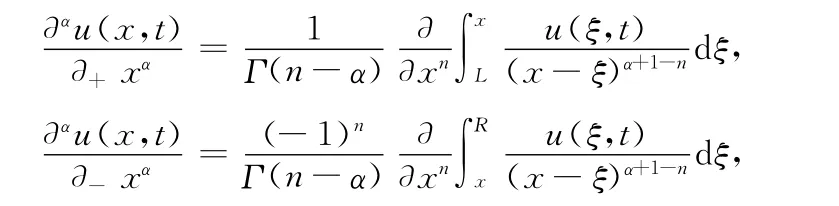
其中0≤n－1＜α＜n（n是整数），Γ（·）是伽马函数。

两边空间分数阶反常扩散方程（1）是一种反常扩散，能够较精确地描述有记忆和遗传、路径依赖性质的物理过程。关于这类问题的数值解法，马维元等对两边空间－时间分数阶扩散方程进行了加权有限差分求解［19］。另外，Meerschaert等分别对单边对流扩散和双边随流扩散方程进行了Grünwald－Letnikov改进型差分求解［20－21］，苏丽娟等给出了双边空间分数阶对流扩散方程的一种有限差分解法［22］。本文根据移位Grünwald－Letnikov公式，将给出方程（1）的隐式有限差分格式，并分析其稳定性。

1 有限差分格式的建立

做网格剖分，令τ和h分别为时间和空间步长，xi＝L＋ih，i＝ 0，1，2，…，N，h ＝；t＝ kτ，k ＝ 0，1，2，…，kM，τ＝。

把式（2）－（4）代入（1），可得到方程（1）对应的隐式差分格式：

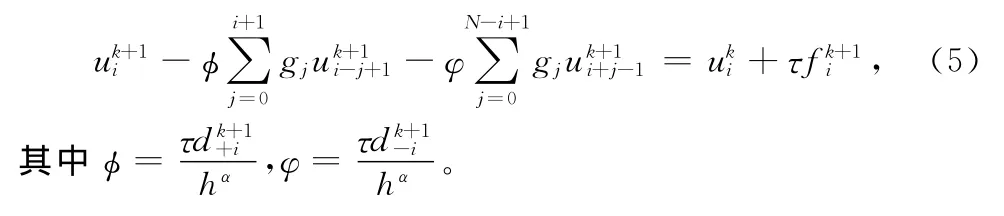
2 稳定性和收敛性分析

引理1 当1＜α≤2时，gj（j＝0，1，2，3，…）具有如下性质：

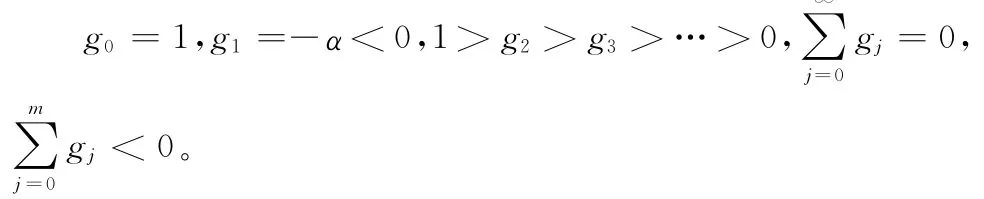
引理2 （Lax等价定理）给定一个适定的线性初值问题以及与其相容的差分格式，则差分格式的稳定性是差分格式收敛的充分必要条件。

引理3 （Gerschgorin定理）设 A ＝ （ai，j）n×n，记rt＝称复平面上的圆域Gi＝ ｛z｜｜z－ai，j｜≤ri，Z∈C｝（i＝0，1，2，…，N）为矩阵A的第i个Gerschgorin圆，称ri为Gerschgorin圆Gi的半径。此时矩阵A∈Cn×n的全体特征值都在它的N＋1个Gerschgorin圆构成的并集之中。

定理1 由式（5）定义的隐式差分格式是无条件稳定的。

证明 将式（5）写成矩阵的形式：AUk＋1＝Uk＋τFk＋1，其中 Uk＝，…，］T，Fk＝ ［，…，］T，A ＝（ai，j）（i，j＝0，1，2，…，N）为系数矩阵，其元素ai，j的定义如下：

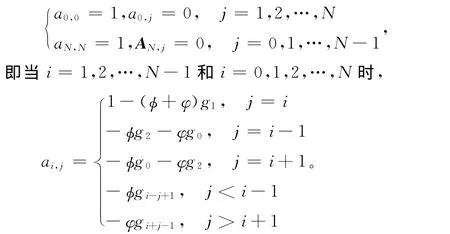
根据引理1和引理3，矩阵A的特征值在以ai，j＝1－（ø＋φ）g1＝1＋（ø＋φ）α为中心，以≤ （ø＋φ）α为半径的圆盘上。故有λ（A）≥ai，i－ri≥1，从而0＜λ（A－1）≤1，所以由式（5）定义的隐式差分格式是无条件稳定的。再由引理2得该方法收敛。

推论1 差分格式（5）的局部截断误差为O（τ＋h）。

推论2 在方程（1）中，当d＋（x，t）变为d＋（x），d－（x，t）变为d－（x）时，定理1的结论依然成立。

推论3 差分格式（5）可推广应用到其他边界条件，如u（L，t）＝0，u（R，t）＋v＝p（t），v≥0，0≤t≤T。

3 数值例子

考虑如下两边空间分数阶反常扩散方程

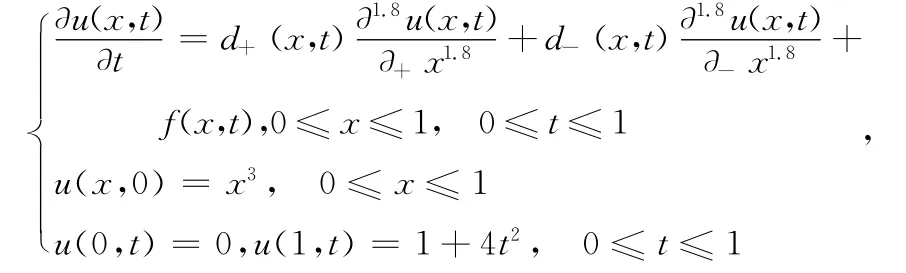
其中d＋（x，t）＝Γ（0.2）x0.8，d－（x，t）＝ 5Γ（0.2）（1－x）1.8，f（x，t）＝－（1＋x）（1＋4t2）x3。此方程有精确解：u（x，t）＝ （1＋4t2）x3。

取定时间步长τ＝0.000 1，空间步长h＝0.02。图1是在t＝0.01时刻由隐式差分格式（5）计算得到的数值解与精确解的比较图，可以看出数值解收敛于精确解。图2是隐式差分格式（5）计算得到的数值解与空间轴、时间轴之间的三维立体图。

4 结论

本文考虑了两边空间分数阶反常扩散方程的数值逼近问题，利用移位Grünwald－Letnikov公式对空间分数阶导数进行离散，构造出了一种计算有效的隐式差分格式，并证明了该差分格式是无条件稳定和收敛的，且具有收敛阶。最后，为了进一步说明文中构造的差分格式是有效的，我们通过数值例子将差分格式得到的数值解与精确解进行了比较，结果表明：差分格式的数值解收敛于精确解，因此文中构造的差分格式是有效的［23－25］。

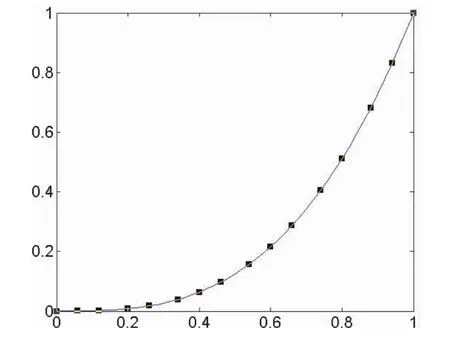
图1 数值解与精确解比较图

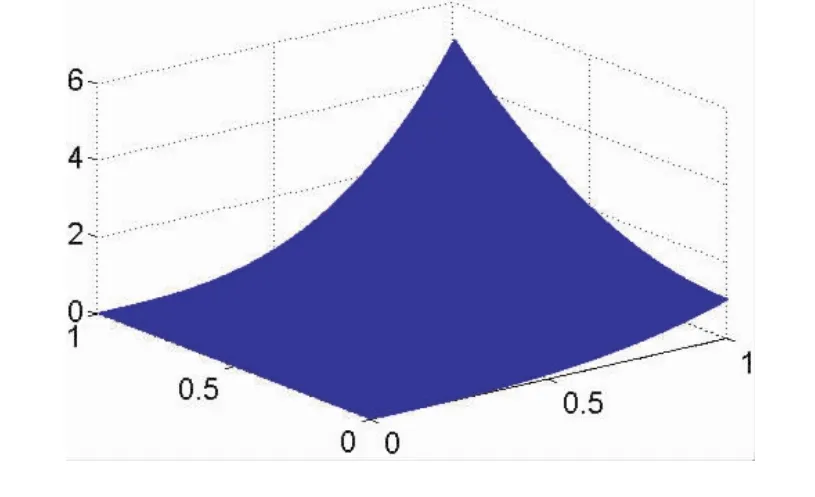
图2 三维立体图

［1］ Tong S J，Zhang W，Chen B Z.Analysis of the pollution consequences on leakage and seepage flow of poisonous liquid［J］.Industrial Safety and Environmental Protection，2006，32（10）：56－58.

［2］ Chen W.A speculative study of 2／3－order fractional Laplacian modeling of turbulence：some thoughts and conjectures［J］.Chaos，2006，16：023126.

［3］ Wang Sheng，Ma Zhangfei，Yao Huqing.Fourierbased series algorithm in fractal diffusion model for porous material［J］.Chinese J Computat Phys，2008，25（3）：289－295.

［4］ Chang F X，Chen J，Huang W.Anomalous diffusion and fractional advection－diffusion equation［J］.Acta Physica Sinica，2005，54（3）：1113－1117.

［5］ 孙洪广，陈文，蔡行.空间分数阶导数“反常”扩散方程数值算法比较［J］.计算物理，2009，26（5）：719－724.

［6］ 马亮亮，刘冬兵.一类n维空间Riesz分数阶扩散方程的解析解［J］.合肥工业大学学报，2014，37（4）：506－509.

［7］ 马亮亮.时间分数阶扩散方程的数值解法［J］.数学的实践与认识，2013，43（10）：248－253.

［8］ 马亮亮.一种Caputo分数阶反应－扩散方程初边值问题的隐式差分格式［J］.贵州师范大学学报，2013（31）：58－61.

［9］ 马亮亮，刘冬兵.一类反常次扩散方程Neumann问题的有限差分格式收敛性分析［J］.五邑大学学报，2014，28（1）：1－4.

［10］ 马亮亮，刘冬兵.变系数分数阶反应－扩散方程的数值解法［J］.沈阳大学学报，2014，26（1）：76－80.

［11］ 刘冬兵，马亮亮.变时间分数阶反应扩散方程的数值分析［J］.江南大学学报，2014，13（1）：109－112.

［12］ 马亮亮.时间分数阶扩散方程的隐式差分近似［J］.贵州师范大学学报，2014，32（2）：79－82.

［13］ 马亮亮，田富鹏.变系数空间分数阶对流－扩散方程的隐式差分近似［J］.中北大学学报，2014，35（1）：11－14.

［14］ 马亮亮.一种时间分数阶对流扩散方程的隐式差分近似［J］.西北民族大学学报，2013，34（1）：7－12.

［15］ 马亮亮.变系数阶空间分数阶对流－扩散方程的有限差分解法［J］.沈阳大学学报，2013，25（4）：341－344.

［16］ 马亮亮.变时间分数阶非定常对流扩散方程的数值分析［J］.辽东学院学报，2013，20（3）：220－223.

［17］ 马亮亮，刘冬兵.一类变时间分数阶含源项非定常奇异摄动对流扩散方程的数值分析［J］.沈阳大学学报，2013，25（5）：424－427.

［18］ Podlubny I.Fractional differential equations［M］.San Diego：Academic Press，1999.

［19］ 马维元，刘华.两边时间－空间分数阶扩散方程的加权有限差分格式［J］.华东师范大学学报，2012（3）：41－48.

［20］ Meerschaert M，Tadjeran C.Finite difference approximations for fractional advection－dispersion flow equations［J］.J Comput Appl Math，2004，172：65－77.

［21］ Meerschaert M，Tadjeran C.Finite difference approximations for two－sided space－fractional partial differential equations［J］.Appl Numer Math，2006，56：80－90.

［22］ 苏丽娟，王文洽.双边空间分数阶对流－扩散方程的一种有限差分解法［J］.山东大学学报，2009，44（10）：26－29.

［23］ 马亮亮，刘冬兵.二维变系数空间分数阶电报方程数值解［J］.辽宁工程技术大学学报，2014，33（3）：429－432.

［24］ 马亮亮，刘冬兵.高维分数阶cable方程隐式差分逼近［J］.辽宁工程技术大学学报，2014，33（4）：544－547.

［25］ 马亮亮，田富鹏.空间分数阶Edwards－Wilkinson方程的显式差分近似［J］.沈阳大学学报，2013，25（3）：250－252.