固定航线的航空自组网连通性研究
罗长远,宋玉龙,高瞻瞻
(解放军信息工程大学 密码工程学院,河南 郑州 450004)
1 引言
根据民航总局的相关数据,我国在2010~2015年间制订了航空运输总周转量、旅客运输量、货邮运输量年增长率为 13%、11%、10%及航空作业量和飞机数量翻番等目标。由于航空业的快速发展,飞机的通信需求也与日俱增,但现阶段的航空通信保障能力不能满足未来航班对空中管制、信息共享等方面的需求。航空自组网(AANET, aeronautical ad hoc network)是移动自组网(MANET, mobile ad hoc network)在航空领域的拓展与应用,其具备自组织、自修复的能力和快速、高效组网的优势,可发挥为空中交通管制提供新的技术手段,为越洋飞行的航班提供有效的通信保障等作用[1]。因此,国内外许多项目及单位对其进行研究,如美国的TTNT、欧盟的 NEWSKY项目、国内的空军工程大学[2]、北京航空航天大学等。
尽管有大量文献对AANET的信道接入技术、路径协议[3]、安全认证[4]等方面进行了研究,然而,对网络可行性与连通性问题的研究较少。可行性与连通性是网络的一个基本而重要的特性,是组网研究的前提,同样也是路由研究的基础。
早在1961年,Gilbert就对无线网络连通性进行研究,但直到1989年这个问题才重新得到重视,对连通性的研究主要通过网络的覆盖问题以及利用随机几何图论、渗流理论等结论和方法。文献[5]通过建立适当的模型分析了节点密度与连通性的关系,但通过节点连通度的指标不足以衡量其他节点的连通性能;文献[6~8]从仿真的角度分别对北大西洋空中走廊、飞机编队、中国大陆空域航班分布情况的连通性进行研究,得到连通分析结果,但缺乏理论支撑;文献[9]对首尾飞机连通性的研究是建立在预先知道中间飞机数量等参数的基础上,而没有考虑飞机动态性和变化性;文献[10~12]仅仅在一维航线上通过建立连通性模型得到的数学表达式均未考虑二维航线的情况及一维航线分层的特点;文献[13]从分层的角度得到一维航线连通概率的数学表达式,但未考虑双向飞行的特点;文献[14]定量表示了二维航空自组网中存在孤立节点的概率与通信半径、运动速率及飞行器密度之间的数学表达式,然而飞机孤立概率并不能完全准确地描述网络连通状况。
针对上述问题,本文将从模型建立、理论推导、仿真实验、实例分析4个层面进行研究。首先,结合实际航线分层、双向的特点,建立一维航线上飞机的分布模型及航线网的航线模型,在考虑飞机密度、航线长度等因素的影响下,推导得出一维航线连通概率的表达式;其次,通过反向飞机对信息的转发作用,引入图论思想建立概率矩阵将多维航线网转化为树状分支和概率图进行研究,进而推导出可以衡量全网连通性的数学表达式;然后,通过仿真对所推导出的理论进行验证,并对我国部分空域及航线在实际飞行场景下的连通性进行仿真分析;最后,为提高航空自组网的连通性,对航班安排等给出了相关建议。
2 模型建立
2.1 一维航线的飞机分布模型
航线的宽度一般为 20 km,而其长度远大于宽度,因此可以将航线等效为一条直线,特别是当同一方向的航线数量较少时,将其称为一维航线。在实际中,由于同一航线的飞机可以双向飞行,所以根据空中交通管制的需要将航线的高度按照飞机飞行的方向划分为奇偶层,层与层的间距为1 km,相邻两层的飞机飞行方向相反。若令其中一个方向为单向航线,则另一方向为反向航线;若根据需要对航线的2个方向同时考虑,则该航线为双向航线。
由于飞机节点的动态性导致实际航线上飞机节点数量往往不是常量。Ehssan S等人[15]在对实际数据的分析后得出了飞机在航线上的分布具有泊松分布特点的结论,并且航线上单向与反向飞行的飞机均服从泊松分布且相互独立。因此,本文将采用泊松分布对一维航线的飞机节点空间分布进行模型的建立。
现假设飞机节点数量在航线长度为l的线段上服从以飞机密度λ为参数的一维泊松分布,并且航线上单向飞行的飞机密度为1λ,反向飞行的飞机密度为2λ。由于单、双向航线上的飞机数量均服从泊松分布,根据泊松分布的可叠加性,得出一维双向航线的飞机数量服从参数为λ1+λ2泊松分布的结论。据此建立的一维航线飞机分布模型如图1所示,其中,ζ为相邻两飞机的距离,R为飞机的通信半径,λ11、λ21为该层上的飞机密度。

图1 一维航线的飞机分布模型
2.2 航线网的航线模型
通过对我国 2010年航班数据统计所绘制的中国城市间民航航班流网络结构[16]如图2所示。其中,边的粗细表示城市间航班数量密集程度。通过对图2的分析可得出以下规律。
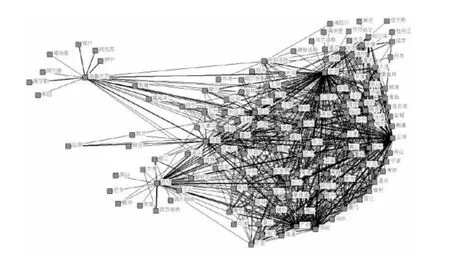
图2 2010年中国民航航班网络
1) 航班流网络具有明显的层次结构,国内航线集中于中东等空域,其中又以北京、上海、广州、深圳的三角地带最为密集,且航线的航班数量较多。
2) 航班流网络结构极不平衡,东中部地区航班比较密集且趋于集团化;西部地区形成了分别以昆明、成都和乌鲁木齐为中心的小集团。
3) 航线与航线之间存在交汇,航线密集且呈网状分布,在网状结构的外围呈树状分布。
本文将这种航线数量较多且航线间相互交叉的航线分布结构称为航线网,并由此建立航线模型图。另外,航线网中每条航线上飞机数量仍符合一维航线的飞机分布模型。
航线模型图建立的具体流程如下。
1) 确定民航飞机的起降城市,据此建立城市集合V(city)。
2) 构建V(city)中具有飞机起降关系的城市间航线集合L( city-city)。
3) 根据L( city-city)中航线的相互关联性产生的航线交叉点,结合城市集合V(city),得到航线模型图的所有节点构成的节点集合V(node)。
4) 节点集合V(node)间的航线构成边的集合L( node)。
如图3所示,航线模型图由树状分支和图共同组成的。其中,度为1的节点与度大于1的节点构成树状分支;航线的交叉点和起终节点度大于1的节点构成了图的顶点V,顶点间形成的边构成了图的边集合L,从而形成图。若令边li的连通概率为pi,便可得到概率图G(pi,V,L) ,在概率图中,用A、B…N…表示图的顶点,用lAB、lBC…表示图的边,用pAB、pBC…表示边的连通概率。

图3 航线模型
3 一维航线连通概率
3.1 假设条件
为方便对一维航线连通概率进行研究与分析,假设条件如下。
1) 所有飞机节点的感知半径与传播半径相等,即为通信半径。
2) 由于飞机的通信半径(几百千米)远大于层与层间的距离(几千米),因此忽略航线上层与层之间的间距,即认为不同层上的飞机均在同一平面上。
3.2 航线l的连通概率
由一维航线飞机的分布模型可知,在l上分布n架飞机的概率为
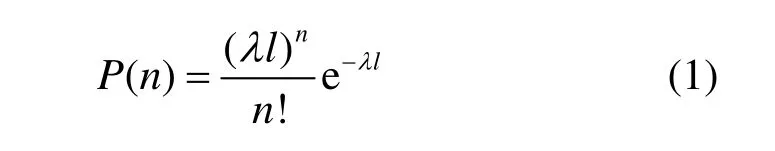
因为航线上飞机数量服从泊松分布,所以两架相邻飞机的距离ζ服从负指数分布,其累积分布函数为
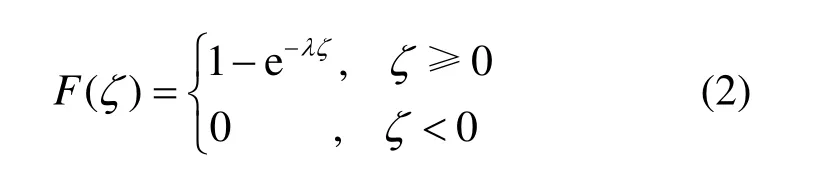
由式(2)可知,两架相邻飞机的距离小于通信半径R时的概率为:P(ζ≤R) =1 - e-λR。当航线l上有n个节点时,若保证航线网络的畅通,只需要相邻的飞机间距离小于通信半径R,并一直延续到整个航线的长度即可,所以当航线l有n个节点且保持网络连通的概率为:

由于航空自组网的连通是指飞机之间的连通,因此,若航线l保持网络连通,则其内的飞机数量至少为2架,结合泊松分布的假设可求得l段内网络连通概率为

受航线上飞机密度λ及航线长度l的影响,一维单向航线上相邻的两架飞机会存在通信盲区、无法连通等情况,进而难以达到全连通状态。而由飞机航线的分层特点可知,若利用航线上反向飞行的飞机进行信息转发,便可以提高航线的整体连通性。根据假设条件,结合同一航线单、反向飞机的分布规律,只需要从整体角度考虑双向飞机数量服从参数为λ1+λ2泊松分布的特点,运用航线l的连通概率表达式便可得到一维双向航线l的连通概率P(λ1,λ2,l),其大小为
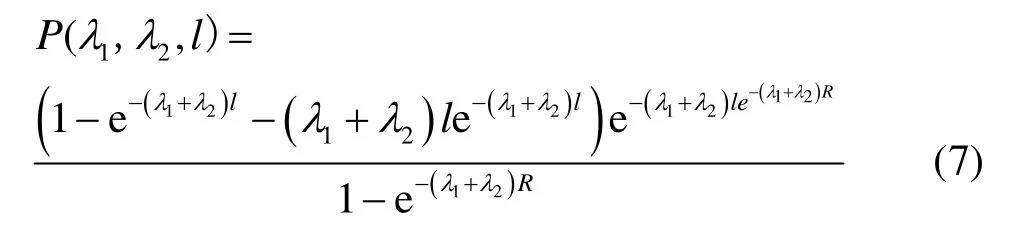
4 航线网连通概率
通过对所建立的航线模型图分析知,如果树状分支都可以与图连通且图本身也是连通的,那么整体网络必然连通。因此,整体网络的连通性便是树状分支与图同时连通性时的情况,而它们之间连通概率相互独立,所以整体网络的连通概率P等于树状分支与图连通的概率PS与图本身连通的概率TP之积,表达式如下

根据实际情况,在一维航线连通理论的基础上,利用双向飞行中的反向飞机对信息的转发作用,运用一维双向航线l的连通概率P(λ1,λ2,l)对PS、PT进行求解。
4.1 树状分枝的连通概率


4.2 图的连通概率
由图论知:若节点A与任意节点连通,则该图必然是连通图。在此基础上,将图的连通概率定义为:各节点与任意节点的连通概率的最大者为该图连通概率。
通过一维航线连通性的分析知航线上的飞机连通概率受λ、l等因素影响,并且航线连通概率相互独立。在计算节点间连通概率时,首先任选节点(如节点 A),并对该节点与其他节点间的路径进行搜索,获得节点间的全部路径;然后利用概率的独立性求出该节点与所有节点连通时的连通概率;再任选除A外的节点,并求出其与所有节点连通时的概率,直至求完任意节点与所有节点的概率;最后比较所得到的概率,其中最大者为该图的连通概率。
4.2.1 初始化关联概率矩阵
定义p ij表示节点i与节点j存在直接路径时的连通概率,其大小主要受飞机密度λ和节点i与节点j之间航线长度l的影响。
依照以下规则构建图的关联概率矩阵[C]m×n:将所要计算的2个节点分别作为第1个和第n个端点;矩阵的主对角线元素全定义为零,即cii=0,i=1,2,…,n;其余元素定义为

4.2.2 消除关联概率矩阵C的所有中间节点
设要消除中间节点k,可按照下面逻辑运算公式计算新的矩阵中的元素


5 实验结果
5.1 实验环境
根据实际航线的相关数据,假设仿真环境为:飞机的飞行区域面积为4 000 km×6 000 km的矩形区域,航线宽度为20 km,长度在[1 000 km,6 000 km]之间;由于飞机通常采用VHF频段进行通信[8],所以其通信半径取值为200 km、300 km、400 km;飞机密度的范围在5×10-3架/km到5×10-2架/km之间。
实验首先设定长度为l的航线和通信半径为R的飞机,然后在Matlab 2009平台上构建飞机密度为λ的泊松分布模型,结合航线方向及适当的飞行速度模拟飞机的飞行场景,其中,飞机的速度由航线长度和飞行时间确定;然后,根据速度生成飞机的位置坐标;最后,计算飞机间距离与通信半径的大小关系,进而求出航线上飞机的连通概率。
5.2 一维航线实验结果与分析
由于某一航线的连通率受飞机的密度λ、飞机通信半径R、航线长度l的影响,因此,需要采用控制变量法进行数据统计及数值分析,最终得到实验结果。具体理论及实验结果如图4和图5所示。

图4 P-λ曲线

图5 P-l曲线
根据图4和图5可知:理论与实验结果的基本吻合验证了一维航线连通理论的正确性。另外,通过对曲线图的分析可知:连通概率随通信半径和飞机密度的增加而增加,当飞机通信半径为400 km、航线长度为 2 000 km时,只需要飞机密度为1.5×10-2架/km时,连通概率便可达到 90%以上;当飞机密度达到3×10-2架/km、通信半径为200 km时,即使航线长度为4 000 km,连通概率也可保持在80%以上,但当航线长度大于6 000 km时,连通概率会较低。因此,可得到以下结论:当飞机提高通信半径或增加航班数量时,网络能保持较高的连通性,但航线长度很大时,即使增加航班数量和传输半径,网络的的连通率也较低甚至会出现很多通信盲区,此时应该采用增加地面基站、卫星转发等手段进行辅助通信保障。
5.3 航线网实验结果与分析
由于航线网连通理论以一维航线连通理论为基础,因此,飞机的λ、R、l这3个因素必然会对航线网的连通性造成影响且对两者的影响效果一致,但除此之外,航线网还受航线条数、航线分布的影响,所以需要从这 2个因素进行对航线网连通性进行实验分析。现取定单条航线长度均为2 000 km的航线网a、b、c,其分布情况示意如图6所示,并采用同样的思路对航线网连通理论进行验证分析,最终得到实验结果。具体理论及实验结果如图7所示。
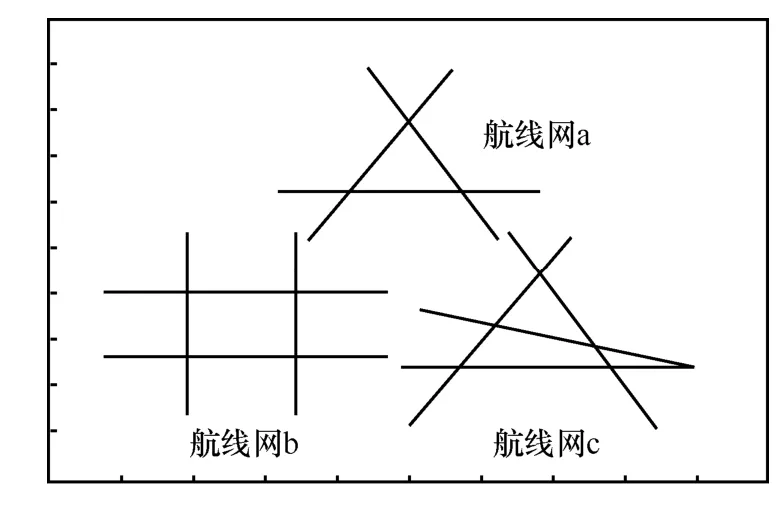
图6 航线网分布示意
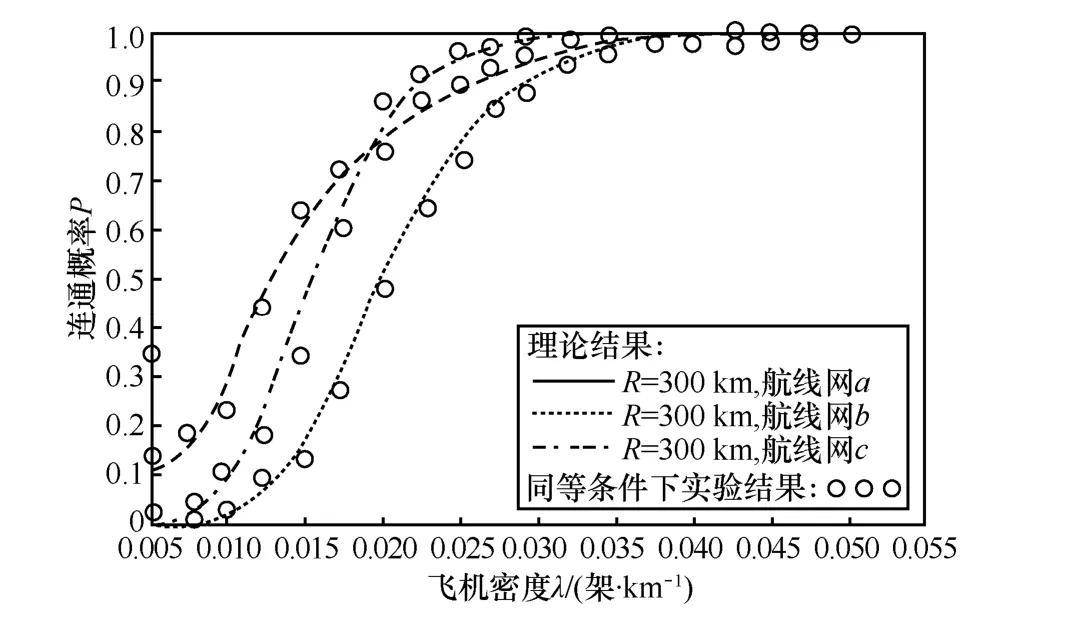
图7 航线网P-λ曲线
根据图7知:理论与实验结果的基本吻合验证了航线网连通理论的正确性。另外,通过对曲线图的分析可知:航线网b的航线数量为4,但航线间所形成的图却没有很多的路径,与航线网a相比,由于增加了航线的总长度,导致同等条件下其连通概率最低;航线网c的航线数量也为4,虽然在飞机密度λ较低时,受航线总长度的影响连通概率较低,但其航线间所形成的图较复杂,所以当λ到达某一值后连通概率相对较高。因此,可得到以下结论:航线网连通性受航线数量和航线分布共同影响,同等条件下,当航线所形成的图越复杂、树状分支越少,其连通性越好。
6 实例仿真分析
6.1 一维空域实例分析
为判断我国航空自组网在一维航线上是否具有现实可行性,本文将根据部分实际航线的航班信息,运用一维连通性数学表达式对单、双向航线的连通性进行仿真分析。按照 2013年北京与三亚之间南北方向部分航线及部分重要航线上的航班信息,根据全天时间内所有航班起飞和降落的时间、地点及其飞行路线,运用Matlab仿真其飞行过程,对其中部分航线上的飞机数量进行统计计算,结果图8所示。
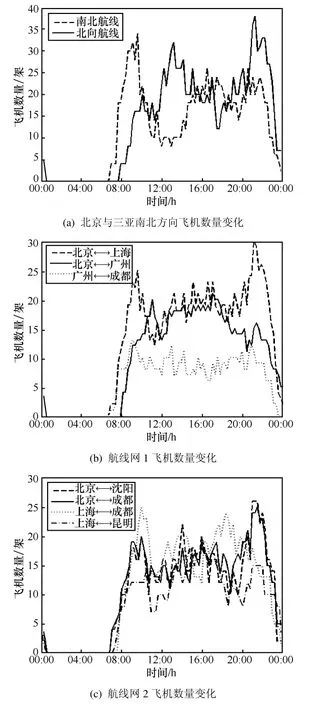
图8 全天时间飞机数量的变化
由于4.2节的实验证明了一维连通性理论的正确性。因此,可以利用所得到的一维航线连通性理论对北京与三亚之间南北方向的部分实际航线进行仿真分析,其仿真结果如图9~图11所示。
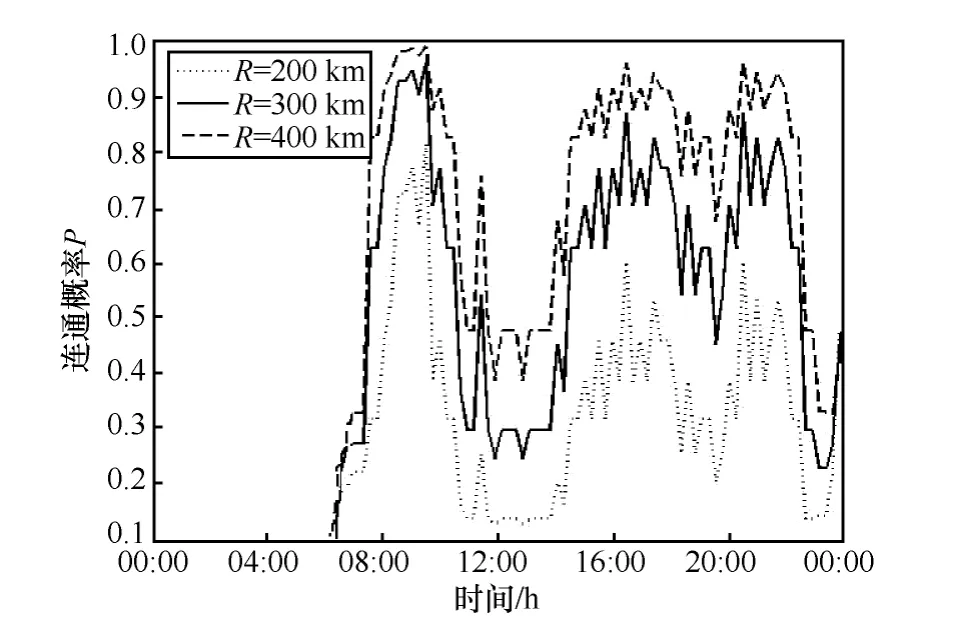
图9 南向航线连通概率
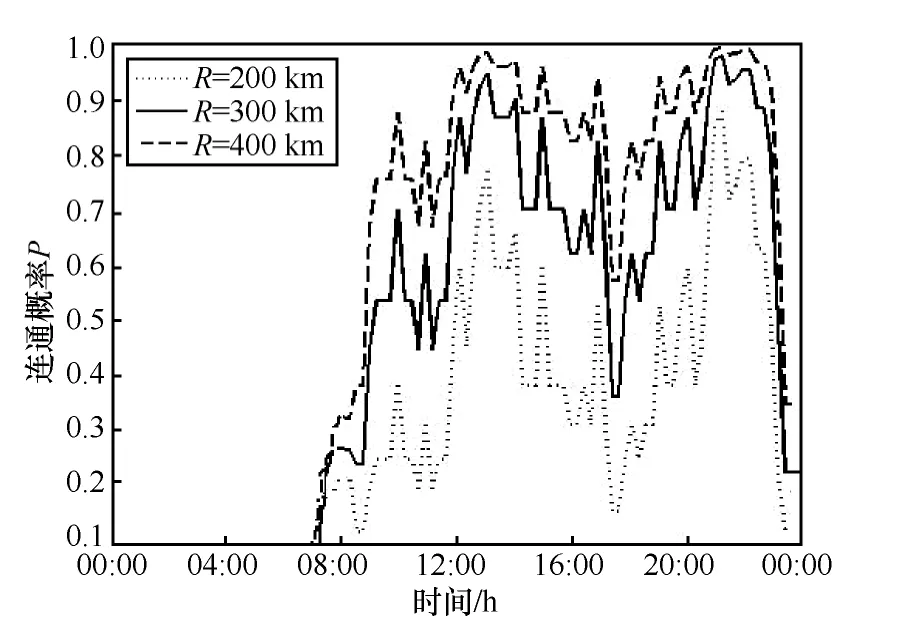
图10 北向航线连通概率
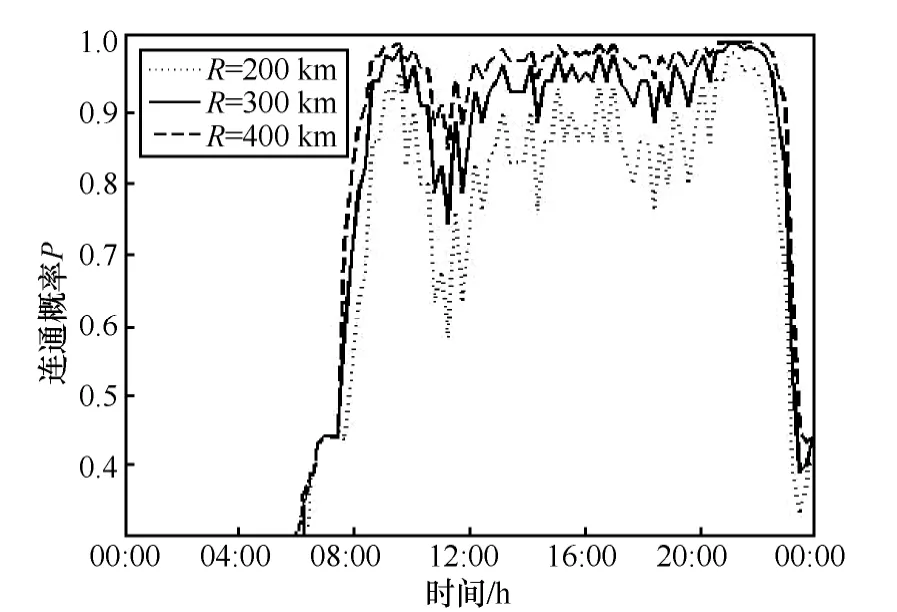
图11 双向航线连通概率
仿真结果表明:单向航线的连通概率与该时刻的航班数量有密切关系,且连通概率曲线与航班数量曲线基本保持一致,例如图 8(a)中南向航线在10:00到14:00之间的飞机数量较少,图9则表现出在对应的时间内连通概率较低,但当飞机数量很少时,连通概率为0;根据图11可知,在同等条件下,由于双向航线可以利用反向飞机进行信息的中转,所以双向航线的连通率要大于单向航线的连通率,特别是当R≥300km时,全天24 h中,北京与三亚之间在8:00到22:00之间有14 h的连通概率保持在 90%以上,甚至部分时间段连通概率达到100%。因此,可得到以下结论:双向航线对于提高网络的连通概率有很大帮助,所以,可以通过合理安排不同方向航班的起落时间以保证同一时间内航线上的飞机密度处于较大值。另外,从连通性的角度表明了上述一维航线上航空自组网的可行性。
6.2 航线网空域实例分析
通过第3节及实验的分析可知,多维航线连通性与航线的数量、长度、位置分布以及航线上飞机密度λ、飞机通信半径R等因素有关。由于不同航线长度l及飞机密度λ均不相同,为简化数据,定义航线长度组[L]={l1,l2,…,ln},现选定航线网1={北京↔沈阳,北京↔上海,北京↔广州,广州↔成都,上海↔昆明},航线网 2={北京↔上海,北京↔成都,北京↔广州,广州↔成都,上海↔成都,上海↔昆明}。
根据图8(b)、图8(c)的相关数据,运用航线网连通性理论对2个航线网的连通性进行仿真,仿真结果如图12和图13所示。

图12 航线网1连通概率

图13 航线网2连通概率
仿真结果表明:航线网的连通率同样表现出随通信半径和飞机密度的增加而增加的特征。在图12中,当R=200km时,在12:00、16:00、20:00出现较低的连通率主要是由于“北京↔沈阳”航线在以上几个时刻飞机数量较小导致的;当R=400 km时,由于此时“北京-沈阳”树状分支航线同样具有较高的连通性,所以整个航线网的连通性均保持在90%以上,由此可知:树状分支的连通性会很大程度地影响整体网络连通性。图 13中,增加了航线数量且减少了树状分支,在同等条件下通过对比发现后者的连通性更高,主要是因为如果航线越密集会造成航线间的交叉点越多,进而导致节点间的通信路径越多,所以整体网络的连通概率较高、连通性较好。由以上结论可知:随着航班和航线数量的不断增加,航空自组网的连通概率会保持较高的水平甚至达到 100%,但支线航班会对全网连通性产生影响。例如:图2反映的中国民航航班网络,全国范围内主要空域航线密集、航线交叉点多、飞机数量巨大,因此,中东部等局部空域航线网的连通性会保持在较高水平,但由于存在一些航班数量偏少的边远航线(如喀什↔乌鲁木齐等),导致整体网络的连通性能受限,此时则需要采用相关的措施用以提高整体连通性。
综上所述,飞机的密度λ、航线长度l、通信半径R、航线的分布是影响网络连通性的关键因素。根据5.1和5.2节的实例分析及其结论,可从以下4个方面采取措施来提高一定空域内航空自组网的整体连通性。
1) 航班安排
合理安排两城市之间航班时刻表,避免过长的飞机起飞间隔以提高一天中航线的飞机密度,从而提高单条航线的连通性。
2) 航线规划
由于单条航线的长度及航线间的分布都会对连通性产生影响,因此需要合理安排航线。若城市间航线长度较大,则可在条件允许的前提下,尽量穿越航线较密集的空域,从而增加航线的交叉点以形成网状结构,达到提高整体连通性的目的。
3) 通信设施
选择合适型号的发射机和接收机,并通过调整天线长度、发射功率和接收灵敏度来增加飞机的通信半径。
4) 辅助设施
针对部分空域航线稀疏、飞机密度较小的情况,可在适当的位置设立地面转发站或卫星中转站,使其可以与附近航线的飞机保持连通。
根据上述建议,可利用航线网连通理论,通过调整不同参数得到连通理论结果,采用多次调整并将结果相对比的方法,便可为提高航空自组网连通性提供具体建议。例如,通信设施调整方面,利用连通模型得到某一区域连通概率为 1,那么在保持其他参数不变的情况下,适当减少通信半径,当出现临界值时便得到了可保持最佳连通效果的最小通信半径,据此最小通信半径的值,调整发射机的发射功率等参数,从而避免能量浪费等问题。
7 结束语
本文讨论了航空自组网的连通性问题。针对航空网络的特点,首先将实际网络抽象为飞机分布模型及航空网的航线模型,运用泊松分布的数学模型得到了一维状态下连通性与飞机密度λ、通信半径R、航线长度l的定量关系;其次,引入图论知识,将航线网的连通性问题转化为树状分支与概率图的连通性问题,从而得到航线网的连通性与航线数量、航线分布等因素的数学表达式,并通过实验证明了一维航线及航线网连通性理论的正确性;然后,运用所得到的理论对我国部分航线进行仿真,仿真结果表明:在我国现阶段的部分空域内,组建航空自组网是可行的;最后,从航班安排、航线规划、通信设施、辅助设施4个方面给出了提高航空自组网连通性的合理化建议。本文的结论对航空自组网的研究与应用具有一定的参考作用,今后还将深入地研究不固定航线的飞机组网情况以及航空自组网的连通性在组网方式、路由选择等方面的应用。
[1] GU W Z, LI J L, HE F J,et al. A delay-aware stable routing protocol for aeronautical ad hoc networks[J]. Journal of Information and Computational Science, 2012, 9(2):347-359.
[2] 郑博, 张衡阳, 黄国策等. 航空自组网的现状与发展[J]. 电信科学,2011, 27 (5): 38-47.ZHENG B, ZHANG H Y, HUANG G C,et al. Status and development of aeronautical ad hoc networks[J]. Telecommunications Science,2011 ,27(5): 38-47.
[3] ZHOU J H, LEI L, LIU W K,et al. A simulation analysis of nodes mobility and traffic load aware routing strategy in aeronautical ad hoc networks[A]. Proc of 2012 9th International Bhurban Applied Sciences and Technology[C]. 2012.423-426.
[4] 黄后彪,罗长远,宋玉龙.航空自组网漫游接入认证方案[J]. 计算机应用研究,2013,30(2):500-502.HUANG H B, LUO C Y, SONG Y L,A authentication scheme for roaming in aeronautical ad hoc networks[J].Application Research of Computers, 2013,30(2):500-502.
[5] BETTSTETTER C. On the minimum node degree and connectivity of a wireless multihop network[A]. Proceedings of the 3rd ACM International Symposium on Mobile Ad Hoc Networking & Computing[C].2002. 80-91.
[6] HOFFMANNF M, AYAZ S,et al. Feasibility of an aeronautical mobile ad hoc network over the north atlantic corridor[A]. The 5th Annual IEEE Communication Society Conference on Sensor[C]. 2008. 109-l16.
[7] CHENG M X. ZHAO Y Y. Connectivity of ad hoc networks for advanced air traffic management[J]. Journal of Aerospace Computing Information and Communication,2004,1(5):225-238.
[8] 郑博, 黄国策, 张衡阳等.甚高频航空自组网的组网概率及连通性研究[J]. 西安交通大学学报, 2011,45(8):24-29.ZHENG B, HUANG G C, ZHANG H Y,et al. Probability and connectivity of a very high frequency aeronautical ad hoc network[J].Journal of Xi’an Jiaotong University, 2011,45(8):24-29.
[9] GHASEMI S A,et al, Exact probability of connectivity one-dimensional ad hoc wireless networks[J]. IEEE Communications Letters, 2006,10(4): 251-253.
[10] 刘丰威,杨胜天,陈雁等.一维无线ad hoc网络的连通性[J].浙江大学学报(工学版),2007,41(8):1335-1340.LIU F W, YANG S T, CHEN Y,et al.On connectivity of one-dimensional wireless ad hoc networks[J]. Journal of Zhejiang University (Engineering Science) ,2007,41(8):1335-1340.
[11] MY N T X, MIYANAGA Y, SAIVICHIT C. Connectivity analytical modeling for a single flight path ad hoc aeronautical network[A]. International Conference on Electrical Engineering/Electronics Computer Telecommunications and Information Technology[C]. Thailand,2010. 51-55.
[12] 郑博, 张衡阳, 孙鹏等. 航空自组网单、双向航路连通性研究[J].上海交通大学学报, 2012,46(4):624-629.ZHENG B, ZHANG H Y, SUN P,et al. Connectivity on one-and two-way flight routes in aeronautical ad hoc networks[J]. Journal of Shanghai Jiaotong University, 2012,46(4):624-629.
[13] JIAN J S, SONG G, LI H,et al. Critical transmission range for connectivity in aeronautical ad hoc networks[A]. Proc of the 10th World Congress on Intelligent Control and Automation[C]. Beijing, China,2012. 4446-4451.
[14] LI H,YANG B,CHEN C L,et al.Connectivity of aeronautical ad hoc networks[A]. Proc of 2010 IEEE GLOBECOM Workshops Aerial Vehicles[C].Miami,2010.1788-1792.
[15] EHSSAN S, ABBSS J. The gobal in fight internet[J]. IEEE Journal on Selected Areas in Communications, 2006,24(9).
[16] 党亚茹, 丁飞雅, 高峰. 我国航班流网络搞毁性实证分析[J].交通运输系统工程与信息, 2012,12(6):177-185.DANG Y R, DING F Y, GAO F. Empirical analysis on flight flow network survivability of China[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(6):177-185.

