土坝坝坡稳定性可靠度分析
邹俏俏
(辽宁省水利水电勘测设计研究院,辽宁 沈阳 110006)
在土坝坝坡稳定分析方面,目前还是采用传统的安全系数法,而把可靠度分析应用到工程设计和现有工程的安全评价上是今后的发展趋势。在土坝坝坡稳定性分析方面,安全系数法是将影响土坝坝坡状态的诸因素看作确定性变量,通过定值安全系数作为衡量土坝坝坡稳定状态的指标。而大量的试验和工程实践证明,影响土坝坝坡稳定状态的因素中有许多具有很大的随机性,如土坝坝坡的强度参数、外界荷载、自然条件、蓄水水位及土体内各种不连续结构面等,由于安全系数方法回避了计算参数的随机性,从而给土坝坝坡稳定性评价带来很大的误差,不少土坝坝坡工程从安全系数角度分析是安全的,但实际运营中却发生滑坡破坏,具有同一安全系数的土坝坝坡实际稳定状态常常不同。而基于随机性分析的土坝坝坡稳定性分析方法是通过建立概率极限状态方程,充分考虑土体参数的均值及其变异性,从实际意义上来说更为合理[1~2]。
对于大型水利工程,在定值安全系数分析的基础上进行可靠度复核,可以提高工程稳定性评价的精度。而一次二阶矩法(FOSM)是常用的方法,包括中心点法和验算点法,现结合定值安全系数与可靠度结合起来分析评价土坝坝坡稳定性的方法。
1 基本理论
1.1 可靠度分析的基本理论
结构破坏的可能性称之为失效概率,以Pf表示,成功的概率为可靠度,以Pa表示,结构在规定的时间内,在规定的条件下具有预定功能的概率称之为可靠度分析,且有Pa=1-Pf,工程设计中,可靠度分析与定值安全系数结合可以提高稳定性分析的精度[3]。以可靠度的角度讲安全系数应满足:Pf·DL<△C,式中:DL为破坏损失;△C为更可靠设计所需造价。可见,当前两者乘积较小时,使用较小的安全系数可大幅降低造价;反之,当前两者乘积较大时,使用较大的安全系数可以避免失事后的损失和善后费用[4]。
有资料显示,在既定的土坝坝坡几何形状下,任何确定的破坏面总存在一个与之相应的安全系数Fs和一个与之相应的Pf。而且,在所有破坏面中,存在一个最小Fs(min)和最大Pf(max)的最危险破坏面。由于基本状态参数是随机变量,具有离散性,所以相应最危险位置并非确定。但在土坝坝坡稳定性问题中把破坏面位置固定而产生的影响并不大,采用基本变量均值确定相应最小安全系数的破坏面作为可靠度分析的破坏面,完全可以满足工程精度要求。
1.2 一次二阶矩法探讨
一次二阶矩法(FOSM)进行土坝坝坡可靠度分析,是在影响土坝坝坡稳定的随机变量的分布尚不清楚时,采用一阶矩(均值)和二阶矩(标准差)的数学模型对土坝坝坡可靠度进行评价。建立功能函数,采用泰勒级数在平均值处将极限状态功能函数展开,使之线性化后求解。
由于土体是一种高度非线性材料,在不同的应力下具有不同的变形特性,因而,如果仍按照结构工程中随机变量互相独立,服从正态分布的可靠度计算,将功能函数在基本变量的均值点上线性化,将出现迭代不收敛现象,影响可靠度评价的成果。
为了提高可靠度评价精度,计算结构可靠指标时,针对土体的一个有效方法就是将随机变量在验算点处“当量正态”化为正态分布。这样就可以采用与一次二阶矩的方法求解结构的可靠性指标,由于此法被国际结构安全度联合委员会(JCSS)所采用,故也叫“JC”法。
1.3 一次二阶矩法的基本原理
假定随机变量已转化为统计独立情况,并进行了等效正态化。将功能函数 g(Y)=(y1,y2,…,yn)在某点 Y*=(y*1,y*2,…,y*n)展开,使之线性化,然后计算功能函数在Y*=(y*1,y*2,…,y*n)的均值、标准差和可靠度。
初始值 y*i=(i=1,2,…,n)通常使功能函数 g(Y)有一个非零的d值:

对于下一次迭代△y*i,认为y*i+△y*i将位于破坏面上,即有:

将上式在y*i展开,忽略△y*i二阶以上小量:

将式(3)减式(1)得:


式中:λi为Cz的特征值,Cz为矩阵值;β为可靠度指标,是一变量,β+△β是下一个变量值。
在上式中忽略△α*iY得:


1.4 一次二阶矩法具体计算步骤[5]:
1)定义 g(X)=(x1,x2,…,xn),假定初始破坏点x*i=(i=1,2,…,n),将其标准正态化为z*i=(i=1,2,…,n),如果xi统计相关,计算得到独立标准化变量y*i=(i=1,2,…,n),并确定β的初始迭代值。
2)将y*i代入式(1)得d值。

4)由式(12)得到△β,把β+△β 作为β 下一次的迭代值。
5)利用上面求得的β,由式(5)和式(10)重新计算z*i=(i=1,2,…,n)或y*i=(i=1,2,…,n)值,作为下步迭代的初始值。
6)重复以上步骤,直至满足收敛条件△β<εβ,d>ε(dεβ,εd为允许误差),这样用一次二阶矩法求解的可靠度收敛效果很好。
2 土坝坝坡稳定可靠度分析计算
2.1 统计相关变量的独立标准化
在可靠度分析中,对随机变量Zi(i=1,2,…,n)的统计相关情况,通常把这些变量通过正交变换转化为独立的标准化变量Yi(i=1,2,…,n),它们的相关系数表示为:

通过正交矩阵T,将Zi变换为不相关变量:
Y=(y1,y2,…,yn)T,Y=TTT
T的列向量为Cz的特征向量,可靠度指标β变为:

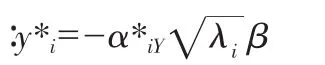

2.2 非正态随机变量的当量正态化
非正态随机变量按照验算点处的累积概率分布函数CDF值和概率密度函数PDF值与原来分布相同的原则当量正态化。很多研究表明,基本变量f服从正态分布,而基本变量c服从对数正态分布,我们需要将其当量正态化[4],具体方法如下:

式中:m′xi,σ′xi,Vxi,X*i,mxi*分别为等效正态分布的均值、标准差、变量xi的变异系数、验算点及变量在验算点处原分布的均值。
2.3 建立土坝坝坡极限稳定状态功能函数及其分析
在定值安全系数法计算的基础上,选定某些参数为基本变量,并令按定值安全系数法得到的安全系数Fs=1,用瑞典圆弧法、Bishop法及Janbu法作为定值分析方法[6],列出相应于各种分析方法的极限状态方程。
1)瑞典圆弧法的极限状态功能函数为:


2)Bishop法的极限状态功能函数为:

3)Janbu法的极限状态功能函数为:

其中:mαi=cosαi+tanφ′isinαi:xi=△Eiti/bi-Eitanαi;△xi=xi+1-xi;Ei为土条两侧法向作用力;Xi为土条两侧切向作用力。
2.4 土坝坝坡极限稳定状态功能函数分析
采用定值安全系数法和一次二阶距可靠度分析法对土坝坝坡进行最危险滑裂面搜索,确定最大失效概率的滑裂面,再反算对应该面的安全系数,从而把定值安全系数法和可靠度分析法结合起来进行对比评价。
针对3个功能函数,对应最大失效概率的滑裂面,不同计算方法得出的安全系数、可靠指标、失效概率是不同的,同时c,φ的相关性也会影响计算结果。经验算比较,瑞典圆弧法得到的可靠指标最小,失效概率最大,Bishop法得到的可靠指标居中,而Janbu法得到的可靠指标最大,失效概率最低。这可以从3种方法的原理上加以解释,瑞典法完全没有考虑土条间的相互作用,Bishop法考虑了土条间的水平作用力,而没有考虑了土条间的垂直作用力。Janbu法同时考虑了土条间的水平和垂直作用力,并且其可靠指标的大小与安全系数的计算结果也具有一致性,彼此结果符合得较好。
考虑土层抗剪强度参数c,φ的相关性时,安全系数与可靠指标及失效概率的计算结果与不考虑其相关性时相差不大,变量之间的相关性对可靠指标的影响很小,可以认为是相互独立的。
2.5 清河水库除险加固工程背水坡坝坡稳定可靠度计算
清河水库是辽宁省省属大型水库,2010年12月水利部大坝安全管理中心对清河水库大坝进行安全鉴定复核,认定为Ⅲ类坝,需要进行除险加固。在除险加固设计过程中,经过水文计算的复核,清河水库大坝需要加高1.15m,经过反复方案对比分析,决定采取带帽加高的方式。为了节省投资,大坝背水坡采取改变原坡比的办法进行加固处理,采用溢洪道尾渠的开挖料填筑。为此,对清河水库大坝背水坡坝坡稳定计算是非常必要的,同时对稳定可靠度进行了计算。出险加固前背水坡比自上而下分别为:1∶2.25,1∶2.25,1∶2.5,出险加固后坝坡坡比分别为 1∶2.0,1∶2.25,1∶2.5;其填筑料为3层,即坝体填筑砂料,溢洪道尾渠开挖料,背坡护坡碎石料。
采用一次二阶矩法进行可靠度计算,设计安全系数1.40。c,φ,γ作为基本变量,概率分布分别采用对数正态分布、非正态分布和正态分布,根据文中所述方法对其数据进行相应转化处理。得出表1的数据。

表1 安全系数及可靠指标计算结果
由表1计算结果看出,不同计算方法得出的安全系数、可靠指标、失效概率是不同的,同时c,φ的相关性也影响计算结果。瑞典圆弧法得到的可靠指标最小,失效率最大;Bishop法居中,Janbu法得出的可靠指标最大,失效率最小。瑞典法没有考虑土条间的相互作用,而Bishop法只考虑了土条的水平力,Janbu法即考虑水平力也考虑垂直力的作用。
3 结语
在土坝坝坡稳定性分析中,考虑分条的作用力可以使其稳定系数、可靠指标有较大提高;影响土坝坝坡稳定性的主要因素是土体抗剪强度指标,内摩擦角的变异性对可靠指标的影响大于内聚力的变异性对可靠指标的影响,可靠指标对内摩擦角的变化更为敏感;变量之间的相关性对可靠指标的影响很小,可认为是相互独立的;在随机变量一定之条件下,可靠指标β随着安全系数Fs的增加而增加。
由于土坝坝坡工程中天然土体材料有较大的变异性,采用安全系数大小来评价土坝坝坡的稳定性,掩盖了土坝坝坡的破坏风险,因而在土坝坝坡稳定分析中引入可靠度分析是很有必要的。虽然土体主要结构面的主要力学参数的取值方法和试验条件差异较大,计算可靠度指标所依据的功能函数也不固定,但由于可靠度分析是以定性分析为基础,可以克服传统定值安全系数分析中的缺陷,因而在定值安全系数计算基础上进行可靠度复核,将其结果作为定值安全系数法的修正和补充,可以更加科学准确的分析土坝坝坡的稳定性。
[1]章建军,陈传尧,揭敏.边坡抗滑稳定可靠性分析[J].华中理工大学学报,1997(04):90-92.
[2]李献民,王永和.黏性土坡稳定的安全系数和可靠度[J].湘潭矿业学院学报,2002(02):82-86.
[3]祝玉学.边坡可靠性分析[M].冶金工业出版社,1993:139-143.
[4]胡向阳.边坡稳定计算中的可靠度分析[J].西北水电,2002(03):12-16
[5]陈祖煜.土质边坡稳定分析—原理方法程序[M].中国水利水电出版社,2003:294-300.
[6]钱家欢,殷宗泽.土工原理与计算(第二版)[M].北京:中国水利水电出版社,1996.

