新型全同步高分辨率DPWM设计

唐 宁，谢颖君

(桂林电子科技大学，广西桂林541004)

数字脉宽调制器(DPWM)已经成为了许多电源转换器的基本构成模块［1，2］。DPWM的频率取决于电源转换器的运行情况。而DPWM的分辨率决定了输出电压/电流控制精度。因此DPWM的分辨率对电源转换器的性能有着至关重要的影响。

1DPWM基本原理和类型介绍

传统的DPWM结构是由一个比较器、一个计数器还有一个RS触发器组成。这种DPWM结构简单，能保持很好的线性度。主要是通过几个预定义的阈值产生电源转换器所需的门控信号。此类设计，最小时间步进等于计数器的时钟周期，分辨率的位数nDPWM可以通过式(1)计算出来。

其中fSW是DPWM的时钟频率，fCLK是计数器频率。为了降低电感和电容的尺寸，现在电源转换器的设计正朝着高的开关频率发展为了更好的数字应用，DPWM分辨率的位数必须大于A/D转换器分辨率的位数。这样可以避免极限环现象。虽然DPWM可以使用计数器和比较器的方法来简单实现，但这种方法的弊端在于，随着DPWM分辨率的提高，所需的系统时钟频率会要求提高的更多。到开关频率f，需要N位的DPWM，而此时的时钟频率需要到达2Nf才能满足系统要求［10］。对于现在的开关电源而言，显然是难以满足的。例如，系统的开关频率达到了1 MHz，需要DPWM的分辨率达到10 bit，此时要求时钟频率需要达到1 GHz。这样不但使设计变得更加复杂还会导致成本的增加。随着半导体技术的发展，SiC和GaN功率管能够使开关频率变得更高，减小了电源转换器的尺寸降低了成本，提高了电源转换器的动态性能和功率密度。然而这些电源转换器都需要高频率高分辨率的脉冲调制器(HRPWM)。HRPWM的另外一个重要的应用是在DC-DC转换器。无论是稳压器模块或者占空比控制输出功率电路，还是功率器件之间的开关延时不匹配需要准确调整。因此电力电子技术和数字控制技术的发展，使更高分辨率的PWM成为必须。

为了克服这个问题，提出不同解决方法。文献［3-9］提到了几种基于FPGA的解决方法。这几种解决方法共同的方案是用一个粗调分辨率的时钟计数器和几个内嵌的时钟管理(DCM)来实现。在计数周期开始时置位PWM信号，然后由计数器和DCM共同作用产生复位信号。除了文献［6，8］，其他论文采用的延时复位信号电路都不是完全同步的设计。异步电路难以进行静态时序分析而且由于FPGA中控制逻辑和走线延时可能产生毛刺。同步设计可以提高电路的可靠信，简化设计过程。除此之外设计可以更加独立于工艺，可移植性强。文献［11-13］的DPWM设计采用的是混合型的设计是无延时的可以达到高的响应速率但是线性度不够。

表1简要的比较了几种不同结构DPWM的主要参数。表格分为粗调计数器频率，实现的分辨率，平衡的路径。平衡路径数越大越难设计单调的DPWM。还指出是否有是同步设计和有无毛刺。

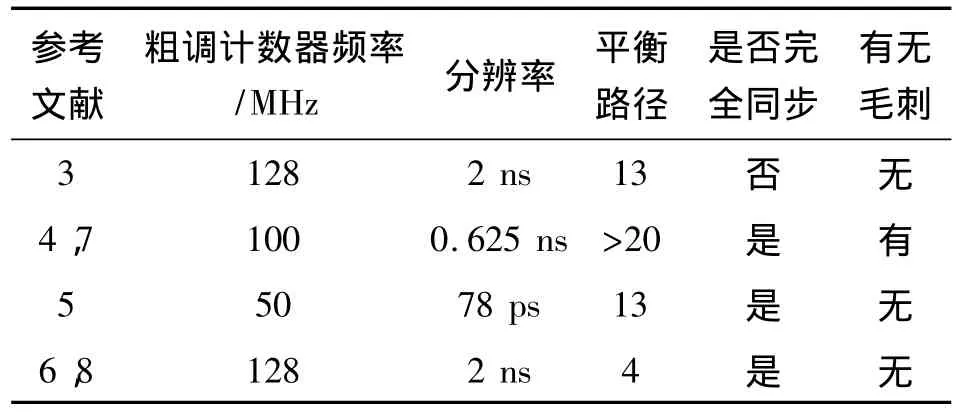
表1 几种HRPWM结构比较

2 完全同步的高分辨率DPWM方案

本文提出一种完全同步的高分辨率DPWM的方案，不仅避免使用不稳定的高频时钟而且提供了更加方便的最终实施。它是基于FPGA内部可用的DCM资源。这种结构的关键部分是FPGA提供的片上DCM。DCM模块框图结构如图1所示，DCM提供4个对输入时钟(CLKIN)的时钟偏移。CLK0是CLKIN的同步信号输出与CLKIN无相位偏移;CLK90与CLKIN有90°相位偏移;CLK180和 CLK270分别与CLKIN有180°和270°的相位偏移。CLKFB是反馈时钟输入，通过反馈时钟可以通过CLKFX输出一定范围的倍频时钟却与输入时钟无相位差。

图1 DCM模块框图

DCM模块具有移动时钟信号相位的能力，能够调整输入输出信号的建立和保持时间，支持对其输出 CLK0，CLK90，CLK180，CLK270 进行相位粗调和细调。最小相移动可以达到1%输入时钟周期的精度并且具有补偿电压和温度漂移的动态相位调节能力。因此到可以得到多个频率相同但相位不同的输出时钟。如图2所示DCM输出时钟的相位调整需要通过属性控制PHASE_SHIFT来设置。PS设置范围为-255到+255，因此最小可以获得1/256输入时钟的相位移动。如果输入时钟为100 MHz，需要将输出时钟调整+0.9 ns的话，PS=(0.9 ns/10 ns)×256=23。如果PHASE_SHIFT值是一个负数，则表示时钟输出应该相对于CLKIN向后进行相位移动;如果PHASE_SHIFT是一个正值，则表示时钟输出应该相对于CLKIN向前进行相移。

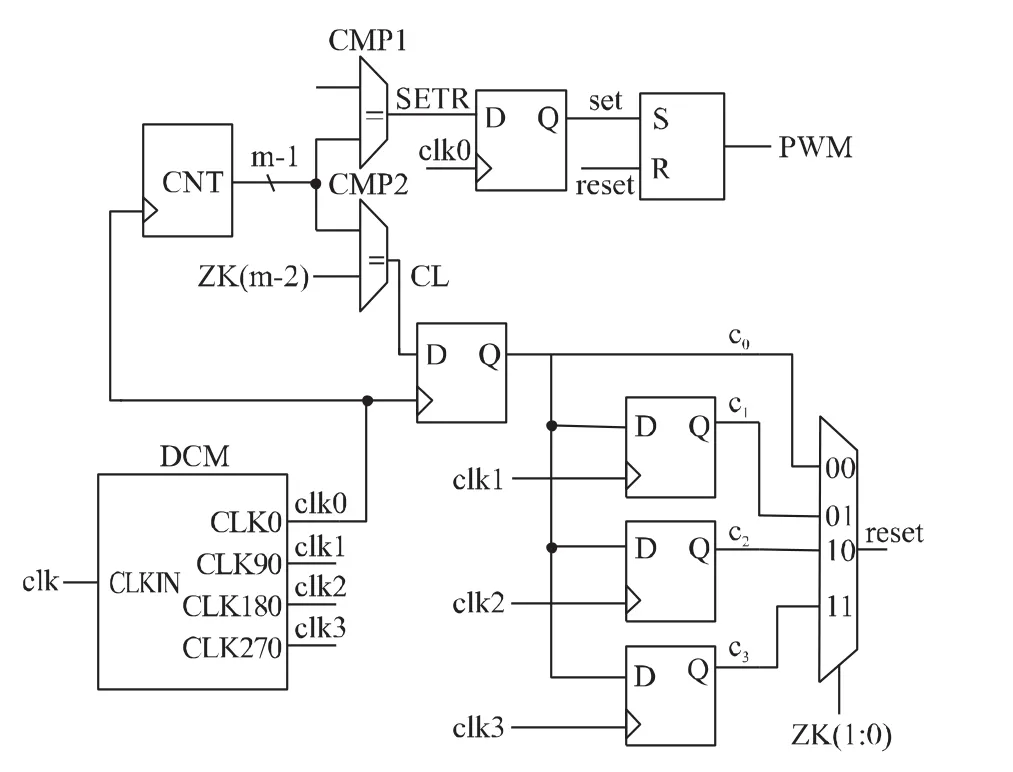
图2 固定精度的相移结果

文献［5］利用DCM的可变相移功能来实现DPWM，然而这方法需要几个时钟周期来改变占空比。降低了DPWM的动态性能。而且采用的是异步电路将时钟分为4个限象。本文提出一种采用DCM固定相移来设计全同步DPWM.。首先介绍基于DCM分辨率为2 bit的DPWM结构。然后在这种结构的基础上延伸出高分辨率DPWM结构。

该结构电路图如图3所示输入时钟clk经过DCM处理后产生4个相位偏移差值为90°的输出时钟。DPWM的占空比是由m+1位的ZK控制。CNT是m-1位计数器。当计数器的值等于ZK(m:2)时，CL信号有效。计数器 CNT等于0而且 ZK(m:2)不等于0时，信号SETR有效。如图4所示当m=4，ZK=“01010”当计数器计 cnt=“010”时，CL信号有效。当cnt=0且ZK≠0时SETR信号有效。4个寄存器实现了一个多相位同步电路，ZK低两位控制多相电路的相移，从图4中可以看出ZK的低两位为“10”选择了clk2。因此在clk2的上升沿将CL信号值赋RS锁存器复位端使pwm输出“0”。这个结构的优点就是数字电路产生的RS锁存器的复位信号是同步的。如果用异步电路来复位RS锁存器就很难进行静态时序分析，而且由于FPGA的控制逻辑和走线原因将很容易产生毛刺。

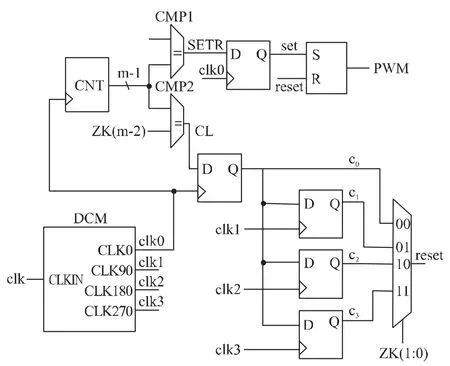
图3 基于DCM的DPWM结构电路图

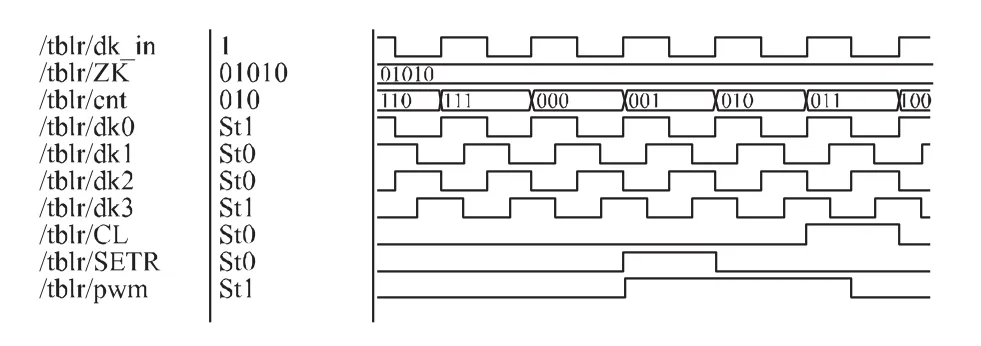
图4 占空比命令为“01010”DPWM波形图

为了提高PWM的分辨率，将提出一种改进的可扩展结构。n=m+k是占空比控制ZK的位数，其中k≥2。该结构包括m位同步计数器，r个DCM，p(p=4×r)个边缘触发器。一个p选一的选择器，以及一个SR锁存器(输出pwm信号)。计数器的位数是可配置的。当计数器等于ZK低m位的值时，clrd有效。计数器的值等于0而ZK≠0时，setd有效。这两个信号产生SET个RESET信号从而控制RS锁存器。计数器和全部的DCM有相同是输入时钟CK。DCM的4 个相移CLK0，CLK90，CLK180，和CLK270 产生一组p个的相移时钟{CKi}其中0≤i＜p，所有的时钟CKi具有相同的时钟周期且占空比都是50%。CKi与CKi-1相位差为TCK/P。最小相移为一个周期TCK的1/256(k≤8)，DCMj的相移值必须设置为j×64/r其中0≤j＜r。图5用p个触发器来实现多相同步电路。FFi是CKi时钟的上升沿触发。p选一的选择器用ZK的低k位来选择CLRi信号来清零SR锁存器。为了提高所设计电路的速度，例如最小允许路径延时，从信号的输入端到输出是不同的。如果忽略相位的值，那么最小路径延时都是TCK/2。该结构的DPWM最大时钟频率只受DCM的影响。因此很容易扩展所需要p的值。从式(2)可以得出该多相同步电路的时序约束没有先前的设计那么严格了，可以实现更高的时钟频率。

其中tpmax(FFi)是触发FFi输入时钟到输出端的最大传输时间，tSU(FFp/2+i)是触发器建立时间。tpmax(net)是路径延时。TCK0/2是CK0与CK4上升沿之间的时间差，δmax(CK0，CK4)是 CK0与 CK4上升沿同时到达的最大时间差。对于一个特定的FPGA系列，p的值取决于DCM模块的可用数量，以及每一个DCM可用驱动的全局时钟线数量而且必须确保多路选择器的输入路径延时小于TCK/p。

图5 多相同步电路

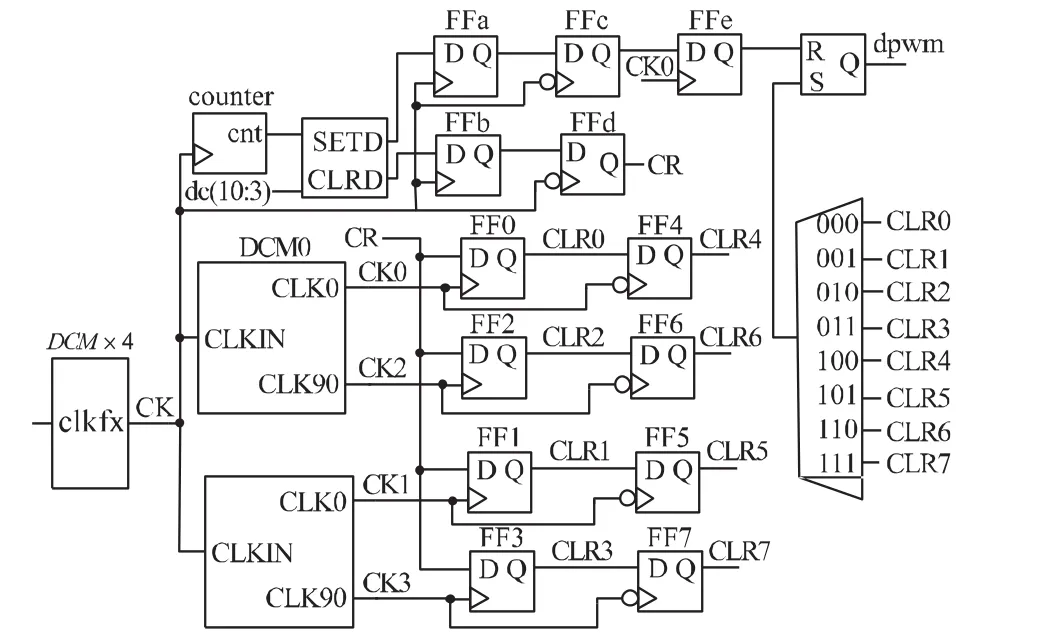
图6 基于DCM的HDPWM结构

3 基于DCM的HRPWM结构具体实现

该结构采用了3个DCM模块来实现高精度DPWM。电路如图6所示该电路图的m=8，k=3。该电路已经用Verlog语言进行实现了。第一DCM把输入时钟进行四倍频得到时钟CK。时钟CK分别作为DCM0和DCM1的输入时钟。Cnt是一个8 bit的计数器，如前面分析的SETD信号和CLRD信号由计数器和dc最高8 bit有效位控制。FFa和FFb储存这两信号。下降沿触发的触发器FFc和FFd主要避免由于CK0和CK2相位反向可能产生的故障。DCM0和DCM1产生8个相位时钟CK0，CK1……CK7(图 6 只标明 CK0，CK1，CK2，CK3)。把DCM1的相移属性值设置为32，那么输出时钟就相移TCK的32/256。在进行引脚绑定的时候需要把DCM0和DCM1绑定在合适的位置。如果采用的是Xilinx XC3S500E Spartan-3E的开发板可以分别将其分配在DCM_X0Y0和DCM_X1Y0，这样可以使它们尽量靠近，避免路径延时。两个DCM可以驱动四个全局时钟线，因此电路必须工作在 CK0，CK1，CK2，CK3的上升沿或者下降沿。FF4，FF5，FF6，FF7必须是下降沿触发。由于占空比的变化在步进时间上引入非线性因素，但是这种FPGA的走线结构解决不了这个问题。这种结构平衡路径为8而且是一种无毛刺的全同步设计电路。

4 实验结果分析

为了验证设计的正确性，将DPWM的输出与开发板的SMA引脚绑定并且通过同轴电缆与示波器相连。为了能在示波器屏幕上完整的显示整个脉冲和最小时间增量，应当选择适当的占空比输入。图7是不同占空比命令输入对应输出脉冲的宽度。从图中可以看出DPWM具有很好的线性度。预期单位占空比变化对应的时间增量Δt为625 ps。由于RESET信号需要经过多相电路而SET信号则直接控制RS锁存器，因此会出现一点偏差。可以通过文献［6］提到的方法降低这种偏差，或者让FFe触发器在CK2的上升沿触发。但是通常数字控制器会这弥补种偏差。

图7 占空比命令从“11000”到“10100”DPWM输出波形

5 结论

本文论述了一种新型全同步DPWM结构并且用Xilinx Spartan-3E FPGA进行实现。该结构的最大时钟频率是由DCM决定而不是多相电路。实验结果表明当输入时钟为50MHz，DPWM的频率为1 MHz，时间分辨率达到了625 ps同时保持了完全同步性。

［1］Wang F，Wei S，Boroyevich D.Voltage Source Inverter［J］.IEEE Ind，2009，15(2):24-33.

［2］Mazumder S K，Sarkar T.Optically-Activated Gate Control for Power Electronics［J］.IEEE Transactions on Power Electron，2011，10(26):2863-2886.

［3］Huerta S C，de Castro A，Garcia O.FPGA-Based Digital Pulse-Width Modulator with Time Resolution under 2ns［J］.IEEE Transactions on Power Electron，2008，23(6):3135-3141.

［4］Batarseh M G，Al-Hoor W，Huang L.Segmented Digital Clock Manager FPGA Based Digital Pulse Width Modulator Technique［C］//Proc IEEE Power Electron，2008:3036-3042.

［5］de Castro A，Todorovich E.DPWM Based on FPGA Clock Phase Shifting with Time Resolution under 100 ps［C］//Proc IEEE Power Electron，2008:3054-3059.

［6］Scharrer M，Halton M，Scanlan T.FPGAbased Digital Pulse Width Modulator with Optimized Linearity［C］//Proc IEEE Power Electron，2009:1220-1225.

［7］Batarseh M G，Al-Hoor W，Huang L.Windowmasked Segmented Digital Clock Manager FPGA-Based Digital Pulse-Width Modulator Technique［J］.IEEE Transactions Power Electron，2009，24(11):2649-2660.

［8］Scharrer M，Halton M，Scanlan.FPGA-Basedmultiphase Digital Pulse Width Modulator Withdual-Edge Modulation［C］//Proc IEEE Power Electron，2010:1075-1080.

［9］Angel de Castro，Elias Todorovich.High Resolution FPGA DPWM Based on Variable Clock Phase Shifting［J］.IEEE Transactions on Power Electron，2010，25(5):1115-1119.

［10］吴铁峰，张鹤鸣，胡辉勇.一种电流模式多输入可控PWM比较器设计［J］.电子器件，2010，33(1):81-84.

［11］周熙，郭健民，李文宏.高精度混合型DPWM设计和实现［J］.半导体报，2007，28(6):967-971.

［12］张祯滨，孙同景，李真.电流型高分辨率DPWM制器的设［J］.电力电子技术，2010，44(12):50-52.

［13］高艳霞，徐妍萍，郭水保.新型混合DPWM方法及其实现［J］.电力电子技术，2009，43(6):84-86.