高斯束展开法的注记:指向性和辐射阻抗的简化计算*
章力军,丁德胜
(1.靖江市计量测试技术研究所,江苏靖江214500;2.东南大学电子科学与工程学院,南京210096)
声波和电磁波的一些辐射或衍射问题可归结于菲涅尔(Fresnel)场积分的求解。例如,超声换能器辐射声场;激光束经过光阑或孔径后的光场分布。然而,在大多数情况下,这一公式是一个二维的、强烈振荡的积分,没有解析形式的解。声场分布通常只能用数值逐点积分或级数展开来计算,计算十分复杂。
高斯束(一般也称基函数或高斯函数)展开方法已广泛应用于快速计算菲涅尔场积分,即声场分布的计算。这种方法的实质是将菲涅尔场积分展开为一系列简单的基本函数的叠加,因而复杂的数值积分简化为一些简单函数(如 Gaussian-Laguerre、Guassian-Hermite、高斯函数等)且项数不多的计算[1-5],计算量大为降低[1-22]。有关这一方法的详细描述可以参考综述文献[22]。
本文给出高斯函数展开法的进一步推广。将文献中的圆形或矩形函数的高斯函数近似展开作为已知的结果,通过简单的数学变换,将贝塞尔函数和一阶Struve函数等特殊函数表示成高斯函数或其他简单函数的叠加。利用这一方法,计算了声学中一类活塞型声源的指向性函数以及均匀活塞的辐射阻抗函数。与直接计算特殊函数值相比,我们的方法给出了相当一致的结果。本文的方法是文献[20-21]研究结果的一种直接推广,作为我们一系列研究报告的一部分。
1 菲涅尔场积分和高斯展开法
在菲涅尔近似或傍轴近似下,圆形轴对称分布的声源的辐射声场可表示为[20-21]
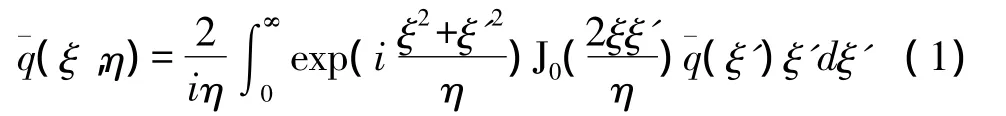
这里,无量纲径向坐标ξ=r/a和η=z/r0.r和z对应为圆柱坐标系中的径向和轴向坐标。瑞利距离定义为r0=ka2/2,菲涅尔距离z0=a2/λ,且r0=πz0.k是波数,λ表示波长。a为声源的特征半径。对于实际的声源,a一般取换能器的半径.式(1)中的传播因子 exp[-i(ωt-kz)]已省略.
Wen 和 Breazeale[4-5]将式(1)中的源分布函数展开成一系列高斯函数的叠加,即
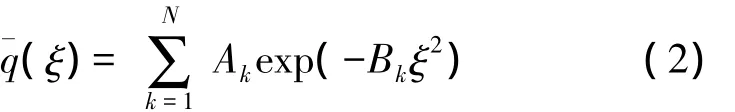
其中Ak和Bk称之为展开系数和高斯系数。对于一给定的源函数,系数Ak和Bk可以用计算机最优化方法来求得。一旦得出这些系数,则场积分化为一组高斯束的叠加:
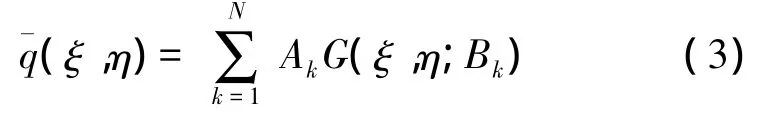
其中
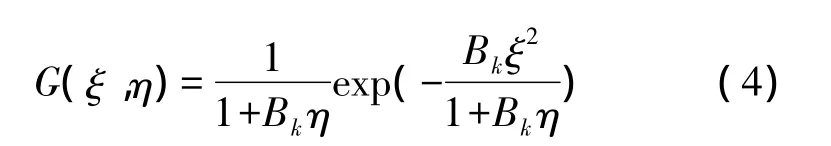
为高斯声源exp(-Bkξ2)的场分布。
Wen和Breazeale给出了两个经典的例子,其中之一为圆形均匀活塞声源的一组展开系数(N=10)[4]。利用这组10项高斯函数,能以相当高的精度计算出圆形均匀活塞的声场分布。在整个声场区域中,除了极靠近声源的近场(<0.12倍的菲涅尔距离)有一定的误差外,高斯函数展开方法所得结果,与直接数值积分计算结果符合很好[4]。
数学上,这一工作意味着圆形函数
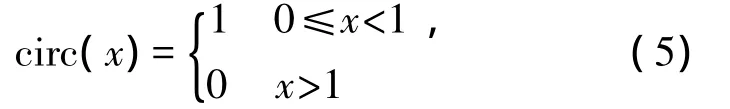
可以在整个[0,+∞)区间上展开一系列高斯函数的近似叠加,即
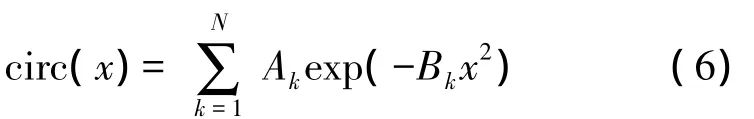
除了上面提到的文献[4]中的表1所列的一组展开系数,文献[5,19]给出了另外两组数据(项数稍多,一组15项,一组25项)。高斯近似展开式(6)在衍射理论中十分重要,可以简化许多复杂问题的计算和分析[6-21]。
以下我们将展开式(6)看作一已知结果,给出一类活塞声源指向性函数和均匀活塞声源辐射阻抗的一种简单的计算方法和结果。
2 指向性函数
根据定义,圆形轴对称活塞声源的辐射指向性函数与下面的积分直接相关:
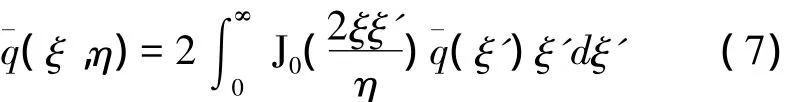
式(7)即远场近似下的夫琅和费(Fraunhofer)衍射积分,可以看作传播距离z或η足够大(趋向无穷远)时,式(1)的极限情形。如通常文献中,式(7)中表示球面波扩散项 exp(iξ2/η)/(iη)已省略。
声学中一类重要的活塞声源的源函数可由下面的函数或这些函数的线性叠加来表示:
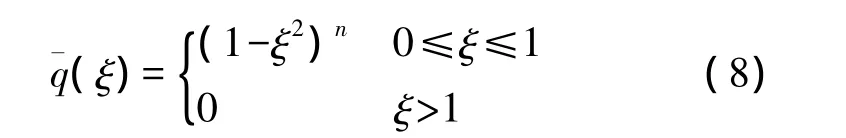
其中n=0对应于圆形均匀活塞声源;n=1和n=2分别对应于最简单的边缘支撑和钳定的活塞声源。将式(8)代入式(7),分步积分并利用贝塞尔函数的积分公式,可得
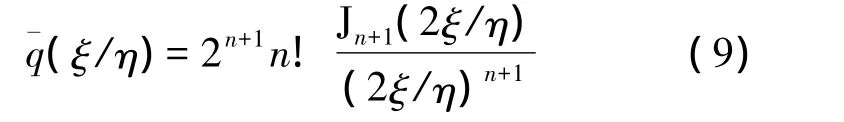
若以球坐标表示,2ξ/η=katanθ,上式可写为
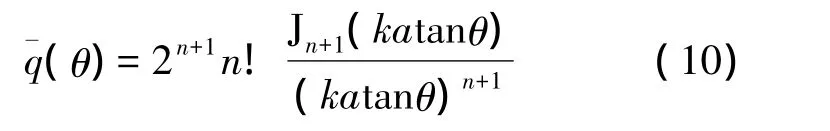
其中归一化波数ka=2πa/λ,θ为方位角。
归一化指向性函数为
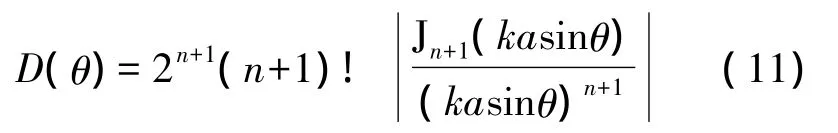
式(9)和式(10)实际上为无限远(离开声源足够远)平面上的声场分布,而远场指向性函数是定义在无限大球面上的。故只需将式(10)中的正切函数换成正弦函数,即得指向性函数式(11)。当方位角不太大时,两者差异并不大。
与文献[20]中推导过程类似,将式(6)视作已知结果,利用傅立叶-贝塞尔变换,可得一般结果
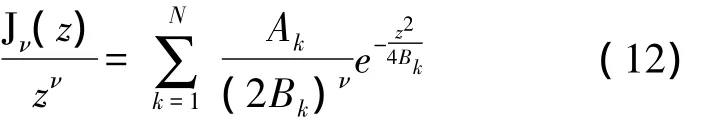
这里要注意的是,式(12)中系数Ak和Bk与式(6)为同一组数据。必然要问式(12)右边的展开精度如何?也就是说,在多大范围内能以较高的精度匹配左边的原函数。文献[20]中的图2给出了一个比较(ν=0,左边即第一类零阶贝塞尔函数J0)。10项高斯展开,在大约0~20区间上,与J0符合很好,相对误差大约1%~2%。而另外一组15项的展开系数[5]在大约0~30的范围内,可以更好地拟合J0。容易验证,ν=1、ν=2的情形与此类似,拟合的区间稍有扩大。
图1给出3种声源的远场指向性函数。图中的曲线分别采用近似展开(12)和直接计算贝塞尔函数所得,可见两种方法所得结果颇相符合。计算中所用的数据为文献[4]中表1所列的一组10项展开系数。对于更大的ka值,如ka=100(主要出现在超声场中),这组展开系数,直到方位角θ≈15°的范围,可以给出准确的指向性函数值。更大角度以外的指向性在超声应用中已不重要。这组10项的展开系数可以满足声学工程中大多数的计算需要。
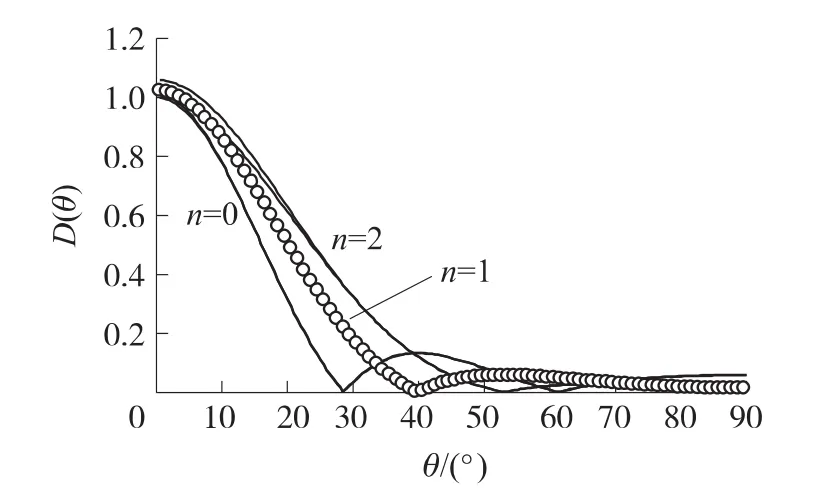
图1 指向性函数ka=8
3 辐射阻抗
众所周知,辐射阻抗是声学中一个很重要的参量,即由于声源振动,声辐射引起的附加于声源的力阻抗。在电声器件的设计中,除了要知道电声器件振动系统的力学参数如质量、弹性系数和力阻外,还必须知道由辐射声场对声源的反作用而产生的附加辐射阻和同振质量。
求声源的辐射阻抗,实际上即求声源振动时,媒质中的辐射声场对声源的反作用力。除了少数几种非常简单的声源,一般情况下,辐射阻抗的计算涉及到双二重积分的求积,通常也是振荡型积分。即便是一些分布和形状的非常简单的声源,如矩形均匀活塞声源,阻抗函数仍为二重振荡型积分。
均匀圆形活塞的辐射阻抗,经前人的努力,归结于阻函数和抗函数(归一化的阻抗函数)的计算。活塞的阻函数
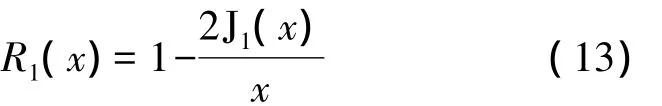
其中x=2ka。抗函数为
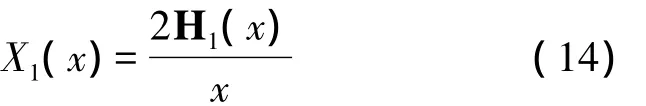
这里H1(x)为一阶Struve函数,其积分表达式
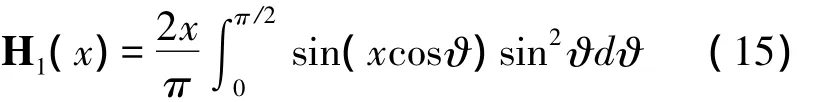
当x<1 或x>10 时,可由式(13)、式(14)的级数展开和渐近展开得出简单而有用的近似解。介于两者之间,无简单的解析近似解。鉴于Struve函数在衍射理论中十分重要,而文献中关于这个函数的计算方法很少,我们给出1阶Struve函数H1(x)的高斯展开。利用式(6),经过一系列的推导,可以得出H1(x)的高斯函数展开(这里没有直接写出,很显然由上面的式(14)和下面的式(16)可以得出),而抗函数表示为
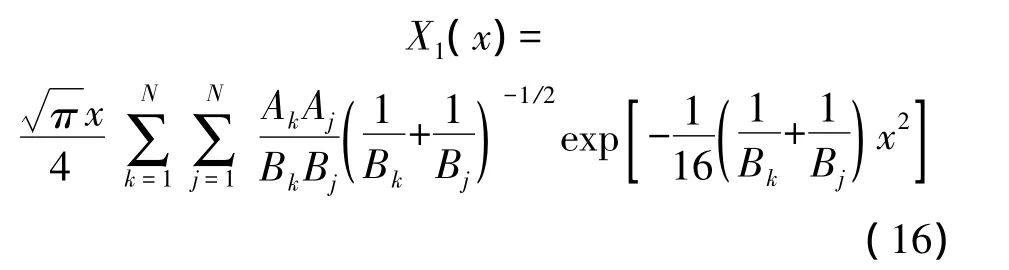
图2给出了活塞的阻函数和抗函数计算结果。其中R1(x)分别采用近似展开(12)和直接计算贝塞尔函数所得,两种方法所得结果颇相符合。对于抗函数X1(x),我们把根据式(16)的计算结果,与课本[23]中x=0(0.5)20的数值相比较,相对误差大约1%~2%。
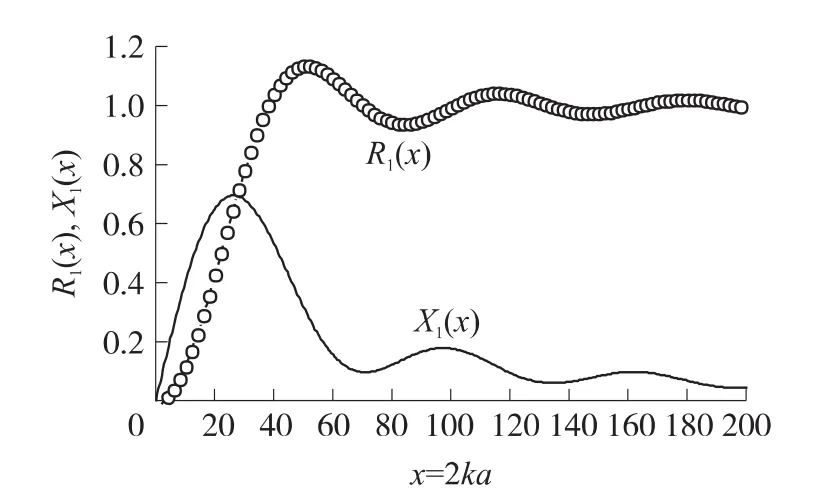
图2 活塞的阻函数和抗函数
4 结语
我们给出了高斯函数展开法的推广,将圆形函数的高斯展开作为已知结果,通过简单的数学变换,将贝塞尔函数和一阶Struve函数表示成高斯函数的近似和。计算了声学中一类活塞型声源的指向性函数和活塞的辐射阻抗函数,与直接计算特殊函数的结果相比,我们的方法给出了相当一致的结果。可以指出的是,本文的方法也可应用于天线辐射等其他问题。一些天线的辐射指向性和阻抗函数,常常可表示为一些特殊函数,利用一些数学变换,这些特殊函数应当可以表示成式(6)或式(12)的类似形式,从而可以简化计算和分析。最后我们指出,本文提供的这些例子,意味着现在的计算方法,可以作为特殊函数计算(精度要求不是太高)的补充。计算精度主要取决于式(6)的展开系数。作者希望我们的应用数学家给出具有更高精度的圆形函数的高斯展开系数。
[1]Cook B D,ArnoultW J,Ⅲ.Gaussian-Laguerre/Hermite Formulation forthe Nearfield ofan Ultrasonic Transducer[J].J Acoust Soc Amer,1976,59(9):9-11.
[2]Cavanagh E,Cook B D.Gaussian-Laguerre Description of Ultrasonic Fields—Numerical Example:Circular Piston[J].J Acoust Soc Amer,1980,67:1136-1140.
[3]Thompson R B,Gray T A,J,et al.The Radiation of Elliptical and Bicylindrically Focused Piston Transducers[J].J Acoust Soc Amer,1987,82:1818-1828.
[4]Wen J J.Breazeale M A.A Diffraction Beam Field Expressed as the Superposition of Gaussian Beams[J].J Acoust Soc Amer,1988,83:1752-1756.
[5]Wen J J,Breazeale M A.Gaussian Beam Functions as a Base Function Set for Acoustical Field Calculations[C]//IEEE Proc Ultras Symp,1987:1137.
[6]丁德胜,林靖波,水永安,等.活塞式超声换能器声场的一种解析描述[J].声学学报,1993,18:245-249.
[7]丁德胜,陆祖宏.活塞类声场的简化算法[J].声学学报(增刊),1996,21:421-428.
[8]Ding D S,Liu X J.Approximate Description for Bessel,Bessel-Gauss and Gaussian Beams with Finite Aperture[J].J Opt Soc A-mer,1999(A16):1286-1293.
[9]Spies M.Transducer Field Modeling in Anisotropic Media by Superposition of Gaussian Base Function[J].J Acoust Soc Amer,1999,105:633-638.
[10]Zhang Y,Liu J Q,Ding D S.Sound Field Calculations of Elliptical Pistons by the Superposition of Two-Dimensional Gaussian Beams[J].Chin Phys Lett,2002,19:1825-1827.
[11]Ding D S,Zhang Y,Liu J S.Some Extensions of the Gaussian Beam Expansion:Radiation Fields of the Rectangular and the Elliptical Transducer[J].J Acoust Soc Amer,2003,113:3043-3048.
[12]Ding D S,Zhang Y.Notes on the Gaussian Beam Expansion[J].J Acoust Soc Amer,2004,116:1401-1405.
[13]Ding D S,Xu J Y.The Gaussian Beam Expansion Applied to Fresnel Field Integrals[J].IEEE Trans UFFC,2006,53:246-250.
[14]Ding D S,Shui Y A,Lin J B,et al.A simple Calculation Approach for the Second Harmonic Sound Field Generated by an Arbitrary Axial-Symmetric Source[J].J Acoust Soc Amer,1996,100:727-733.
[15]Ding D S,Lu Z H.A Simplified Calculation for the Second-Order Fields Generated by Axial-Symmetric Sources at Bifrequency[C]//Proc of the 14th Inter Symp on Nonlin Acoust.1996:183-188.
[16]Ding D S.A Simplified Algorithm for the Second-Order Sound Fields[J].J Acoust Soc Amer,2000,108:2759-2764.
[17]Ding D S,Zhang Y.A Simple Calculation Approach for the Second-Harmonic Sound Beam Generated by an Arbitrary Distribution Source[J].Chin Phys Lett 2004,21:503-506.
[18]Ding D S.A Simplified Algorithm for Second-Order Sound Beams with Arbitrary Source Distribution and Geometry(L)[J].J Acoust Soc Amer,2004,115:35-37.
[19]Kim H J,Schmerr L W,Sedov A.Generation of the Basis Sets for Multi-Gaussian Ultrasonic Beam Models—An Overview[J].J Acoust Soc Amer,2006,119:1971-1978.
[20]Ding D S,Tong X J,He P Z.Supplementary Notes on the Gaussian Beam Expansion[J].J Acoust Soc Am,2005,118:608-611.
[21]Dai Y R,Ding D S.Further Notes on the Gaussian Beam Expansion[J].Chin Phys Lett,2012,29:024301.
[22]Ding D S,Liu X J,Huang J H.Progress of Acoustics in China[M].Cheng J C,Tian J,eds.Bejing:Science Press,2008:55
[23]杜功焕,朱哲民,龚秀芬.声学基础(下)[M].上海:上海科学技术出版社,1981:288.

