基于全变分的模糊人脸图像复原算法
魏雪飞,葛成伟
(南京工业大学电子与信息工程学院,南京211816)
在人脸图像采集过程中,采集到的图像往往会出现亮度失衡或者模糊的现象。影响图像清晰程度的因素很多,如拍摄过程中的抖动、聚焦不准、曝光过度或不均以及摄像头和景物之间的相互移动,都会降低图像的质量,这一质量下降的过程称为图像的退化。为在复杂环境下进行人脸图像采集的任务,有必要引入图像复原技术。图像复原技术是尽可能解决受到外界干扰所引起的图像模糊问题,复原质量的好坏很大程度上决定了人脸检测和特征提取的效果。
图像复原是图像处理领域的一个经典问题,研究者在硬件技术和软件技术方面提出了很多解决方法。硬件角度上,视频芯片和摄像机生产商提出了防抖动、运动补偿的方案。软件角度上的研究比较充分,早期就有逆滤波法、最小均方误差滤波法、约束最小二乘方滤波法等一些经典复原算法。由于图像复原问题是一个病态求逆过程,将会导致无解或者解的不唯一性。目前研究比较成功的是Chan等人的变分正则化方法[1-3],即利用原始图像的局部平滑、非负性和能量有限等先验知识,将复原问题转化为一个最小代价函数的优化问题。文献[4]提出优化-最小求解的方法解决了邻域像素的变分问题,改善信噪比指标达到2 dB左右。
本文在充分结合人脸图像采集过程的基础上,根据全变分正则化的思想,引入相容点集的概念,提出一种有约束的人脸图像复原算法,并使用最速下降算法求解,初步实现了模糊图像复原的预处理过程。
1 图像复原全变分模型
图1是一个通用的图像退化和复原模型[5]。在这个模型中,图像退化的过程可以建模为作用在一帧原始图像f(x,y,n)(以下简写为 f(n),n为帧号)上的退化函数h(x,y,n)(以下简写为 h(n)),与一个噪声 η(x,y,n)(以下简写为 η(n))联合作用产生了退化图像g(x,y,n)(以下简写为g(n))。根据这个模型,图像复原就是要在给定g(n)相关信息的基础上,得到f(n)的近似(以下简写为

图1 图像退化及复原模型
上述退化模型的数学表达式可以表示为
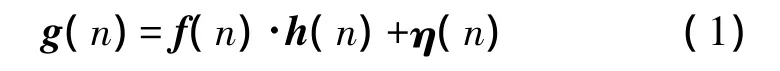
式中,f(n)为一帧原始图像,h(n)即为退化因子,η(n)为随机噪声,g(n)为采集到的图像;·表示线性卷积。为了方便研究,暂时不考虑随机噪声。设f(n)的尺寸为M1×N1,h(n)的尺寸为M2×N2,且图像模糊前后无能量损失,即有,式(1)变为
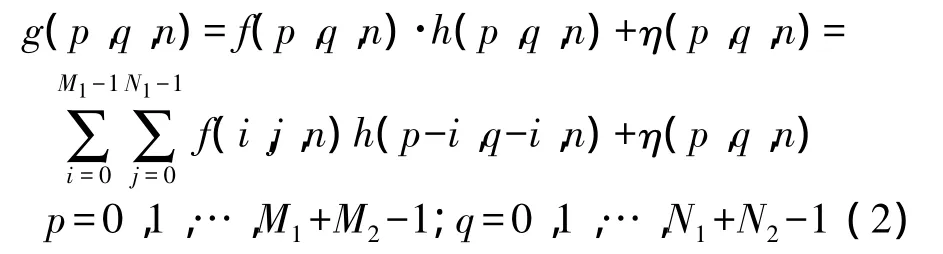
构造复原模型:

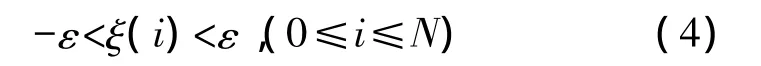
ε是事先确定的误差界,可以取ε=1。
根据上述分析,可以得到,图像复原本质上是求^f,其关键在于求h。这是一个病态的求逆过程。如果h等于0或者很小的时候,噪声将被放大,因此任何一种图像复原算法都要考虑当出现病态性时如何控制噪声对复原结果的干扰。
本文使用全变分因子,构造模糊图像复原模型,提出了一种基于全变分的模糊人脸图像复原算法,这种算法通过引入点集的概念进行归类,并使用最速下降法求解该模型。实验结果表明,这种转化实现了模糊图像的复原。
考虑图像的采集过程,构造全变分约束模型[3]
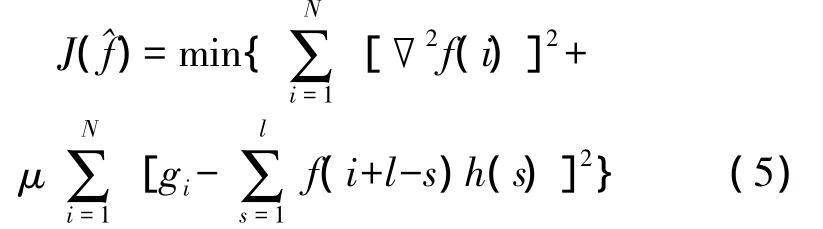
在已经得到初始估计h(0)和初始估计f(0)之后,进一步改进有关估计。记第k帧的图像估计和模糊因子估计为f(k),h(k)。在每次迭代过程中,式(4)不一定均满足,为了表示这些约束条件的不同情形,引入点集记号如下:
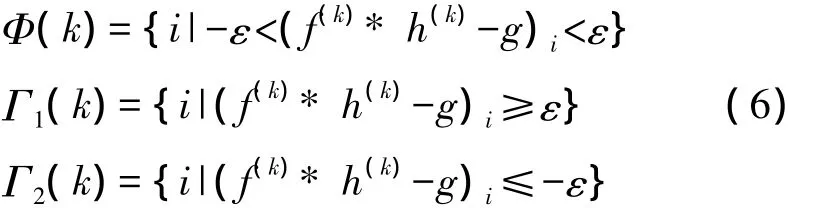
由此得到点集:Φ(k),Γ1(k),Γ2(k),(k=0,1,…),Γ1(k),Γ2(k)表示第k次迭代时不相容的点集,Φ(k)表示第k次迭代时的相容点集。因此,优化式(5)可以得到:
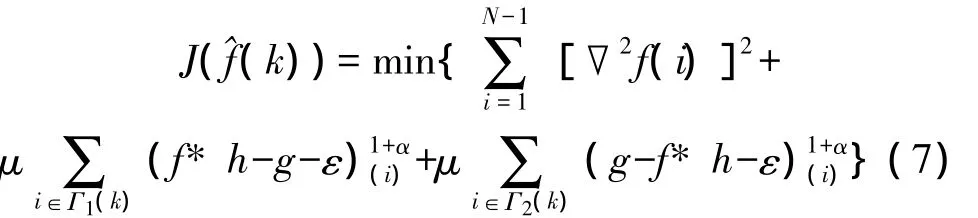
其中α是一个惩罚因子,可以是很小的正参数(暂假设α=0.01),为了计算方便也可令α=0或α=1。当α越大时,惩罚越厉害。
如果一个图像具有快速变化点或是跳跃点,那么其频域的高频成分会比较大。为了体现图像的跳跃程度,在原目标函数加上约束项:

f(ω)为原始图像f(n)的傅里叶变换。表示图像在频域上的总能量,由经验知近似表示跳跃对应的能量。
上述表达式中既有时域函数,又有频域函数,为了便于计算,利用Parseval公式统一转化为时域函数,有
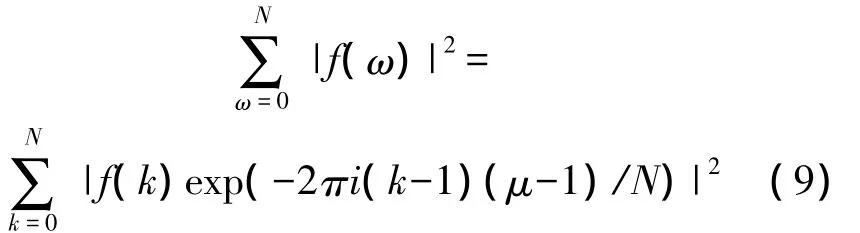
最后将图像平滑性与跳跃性结合在一起,进一步改进,得到优化的目标函数为:
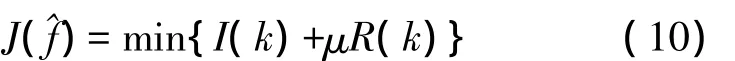
其中
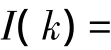

其中I(k)是图像恢复的清晰度因子,R(k)是图像获取因子。
对于上面给定的目标函数优化问题,可以归结到求解一种搜索迭代过程。在搜索迭代中,将前一帧的跟踪结果作为后一帧的初始化输入。每一次搜索后,目标函数和约束条件都要改变。具体的算法流程:首先利用式(11)计算下降方向,再根据目标函数确定步长。最后,检验新的图像估计是否满足有关约束,并由此改变目标函数及约束条件,如此循环。
使用最速下降法[6]在求解上述最小化模型中,需要得到目标模型的下降方向和下降步长。为了统筹考虑原始图像及模糊因子的误差大小,引进变量的增量δf,δh,记关于f和关于h下降方向分别为:δf=-∂J/∂f,δh=-∂J/∂h。采用线性搜索的方法计算新的目标点:

其中λ是由约束条件确定的沿下降方向的前进步长。
对于迭代步长λ,在每次迭代过程中希望相容点集保持稳定,并且希望有更多的不相容点集变为相容点集,即
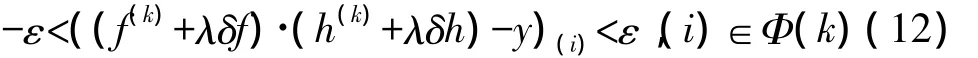
这是一个关于变量λ的二次方程,根据根的判别式法可以判定是否有解。
对于每一个(i)∈Φ(k),一定能有一个可行的步长,即大于零的步长保证目标函数下降,同时下降步长的不能太小,因此,在下降方向搜索步长的最小值:

另一方面,还需要约束步长不要过大,避免出现从一个不可行点集到另一个不可行点集的情形,即
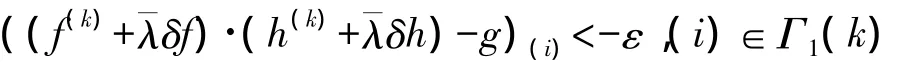
和
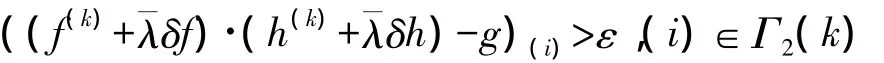
为此,由

计算得
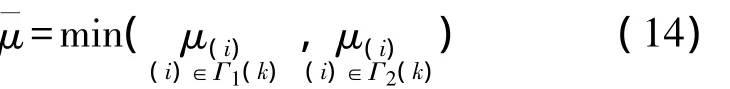
2 实验结果及分析
为了测试本算法对模糊人脸图像复原的有效性,采用ORL图像库的一个子集进行测试。对受到一定噪声污染的模糊人脸图像(为方便起见,将图2三人自上而下命名为甲、乙、丙),使用本算法对其进行复原,对比结果如图2所示。

图2 图像复原效果
图2(a)、2(b)、2(c)列显示了设定参数μ分别为1、0.5和0时,本文算法对模糊人脸图像的复原效果((a)、(b)、(c)列分别为甲、乙、丙复原前后的图像)。μ是平衡参数,权衡总有界变差项与总观测误差项的比值,如果μ取值过大则残留较大的噪声,取值过小则模糊不能完全去除。(a)两列的人脸图像,引入噪声比重较大,虽然复原得到的图像仍存在残余噪点,但是图像边缘相对清晰了很多;(b)两列图像受到的噪声干扰减小,复原后的图像也逐渐逼近原始图像;(c)两列再次加大信噪比,复原图像存在较多的伪影和振铃,但是仍然清晰显示了人脸的轮廓。实验结果表明,无论是有无噪声污染情况下,经过复原得到图像都能反映原始图像。
为进一步说明图像的复原效果,采用图像复原质量的评价标准模型[7]中的峰值信噪比(PSNR)公式对上述结果进行定量评价:
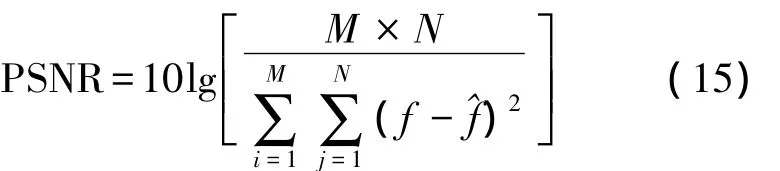
计算原始图像与复原图像的PSNR,结果如表1所示。
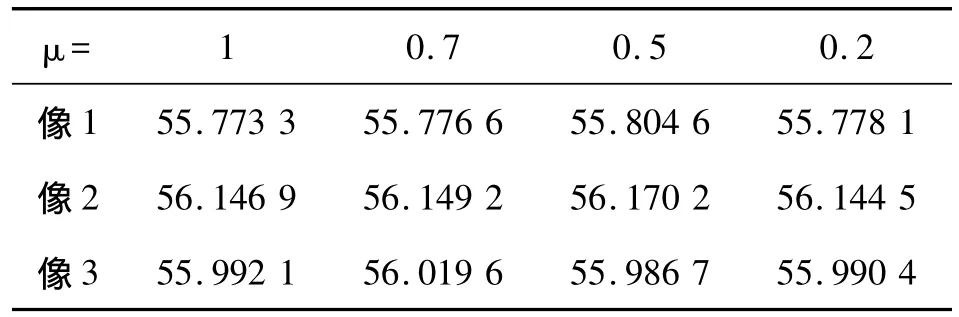
表1 复原信号与原始信号的PSNR
通常PSNR越大,说明图像复原得越好。表1中的PSNR数据也表明本文算法的有效性。同时可以看到参数μ是影响信号复原效果的关键因素。
3 结论
针对退化模糊的人脸面部图像,本文研究了图像在采集过程中退化的原因,给出了一种基于全变分的最优化算法,并使用最速下降法进行迭代求解。这种算法基本上重现了原始图像,为后续的人脸检测、跟踪和行为理解等提供了一个理想的画质。
[1]Chan T F,Wong C K.Total Variation Blind Deconvolution[J].IEEE Transaction on Image Processing,1998,7(3):370-395.
[2]石明珠,许廷发,张坤,等.运动成像混合模糊的全变分图像复原[J].光学精密工程,2011,19(8):1973-1981.
[3]Terrence Chen,Wotao Yin,Xiang Sean Zhou,et al.Total Variation Models for Variable Lighting Face Recognition[J].IEEE Transactions on Pattern Analysis and Machine Inelligence,2006,28(9):1619-1524.
[4]徐梦溪,徐枫,黄陈蓉,等.优化最小求解的广义总变分图像复原[J].中国图象图形学报,2011,16(7):1317-1325.
[5]魏雪飞,葛成伟,陆建明,等.基于线性规划的分段平滑信号的复原算法[J].信号处理,2012,28(8):1200-1206.
[6]Abdellatif M.A Regularized Hybrid Steepest Descent Method for Variational Inclusions[J].Numerical Functional Analysis and Optimization,2012,33(1):39-47.
[7]吴显金.自适应正则化图像复原方法研究[D].湖南:国防科技大学,2006.
[8]Li Bei,Que Dashun.Medical Images Denoising Based on Total Variation Algorithm[J].Procedia Environmental Sciences,2011,8:227-234.
[9]肖亮,韦志辉,吴慧中.基于最大后验概率和鲁棒估计的图像恢复推广变分模型[J].计算机研究与发展,2007,44(7):1105-1113.
[10]叶嘉鲁,李福德,肖伟,等.含噪声的运动模糊图像点扩散函数尺度鉴别[J].电子器件,2007,30(2):593-595.
[11]Aubert G,El Hamidi A,Ghannama C,et al.On a Class of Ill-Posed Minimization Problems in Image Processing[J].J Math Anal,2009,352(1):380-399.
[12]Quiroz E A,Quispe E M,Roberto Olivera P,et al.Steepest Descent Mmethod with a Generalized Armijo Search for Quasiconvex Functions on Riemannian Manifolds[J]J Math Anal,2008,341(1):467-477.

