基于双对数压缩模型的真空预压非线性固结解
韩文君 刘松玉 章定文 刘维正
(1东南大学交通学院, 南京 210096)(2常州市轨道交通发展有限公司, 常州 213022)(3中南大学土木工程学院, 长沙 410075)
真空预压法是一种优良的地基加固方法.工程设计中,常采用砂井固结理论研究真空预压固结过程[1-2].Schiffman等[3]给出了砂井非线性固结解答;Hansbo等[4]采用水力梯度和渗透速度的指数关系来反应土体固结过程中渗透系数变化过程;Indraratna等[5]引入孔隙比e与有效应力σ′、孔隙比e与水平渗透系数kh的关系式,得到了正常固结土和超固结土的非线性固结解答;周琦等[6]采用e-σ′及e-kh关系式,研究了砂井地基正常固结土固结性状;董志良[7]建立了真空预压加固地基固结方程;Indraratna等[8]假定砂井内超静孔压(负压)沿竖向呈线性衰减分布,求得整个地基的平均超静孔压;彭劼等[9-11]提出了考虑真空荷载实际边界条件的固结解答.但是,已有的解答都未能同时考虑真空荷载实际边界和土体固结参数变化的特性.
本文在文献[5-6,10]的基础上,考虑真空荷载沿深度衰减的实际边界条件,引入能对土体压缩曲线进行线性化的双对数坐标lg(1+e)-lgσ′及lg(1+e)-lgkh,建立了真空预压砂井地基非线性固结近似解答.
1 真空预压砂井固结计算模型
1.1 基本假定及求解条件
完全打穿砂井地基固结的计算简图见图1.假定土体满足等应变条件,土中水的渗流服从达西定律;任意深度z处,从土体中流入砂井的水量等于砂井中向上水流量的增量.涂抹区与未扰动区的土体除渗透系数不同外,其他性质相同.真空荷载为瞬时荷载,固结过程中为常量.图1中,dw,rw分别为砂井直径和半径;ds,rs分别为涂抹区直径和半径;de,re分别为砂井影响区直径和半径;r为距砂井中心距离;H为土层厚度;p0为膜下真空荷载的绝对值;kl为真空荷载衰减系数.

图1 砂井地基径向固结轴对称问题的计算简图
根据文献[12],砂井地基仅考虑径向固结时的基本控制方程为
(1)
(2)

(3)

井周的流量连续方程为
(4)
式中,uw为排水板内任一深度的超静孔压;kw为排水板渗透系数.
式(1)~(4)的边界条件如下:① 当r=re时,∂ur/∂r=0;② 当r=rs时,ks∂us/∂r=kh∂ur/∂r;③ 当r=rs时,ur=us;④ 当r=rw时,us=uw;⑤ 当z=0时,uw=-p0;⑥ 当z=H时,∂uw/∂z=p0(1-kl)/H.

1.2 固结方程的推导
整个地基的平均超静孔隙水压力值为
(5)
将式(1)和(2)两边均对r积分,结合边界条件,将积分结果代入式(5)可得[8]
(6)
整个土层平均固结度为

(7)
式中,Ru为无量纲的中间变量.
将式(6)代入式(7),整理后可得[5]

(8)
式中,σ为土体总应力.


(9)
式中,Th为时间因子;ch0为土体的固结系数;e0为土体的初始孔隙比;mv0为土体的初始体积压缩系数;kh0为土体的初始水平渗透系数.
引入反应土体固结非线性的双对数模型,以便在同一坐标系下建立固结方程,即[13-14]
(10)
(11)

对于正常固结土,将式(10)对σ′求导,可得[6]

(12)
将式(12)联合式(10)、(11),代入式(9),可得

(13)


(14)

式(14)是含有变量Ru的非线性偏微分方程,该方程没有通解.由于0≤Ru≤1,则

(15)
式中,Wav为W的极限平均值.


(16)
古筝合奏曲在历史中有很多,但大多是和其他的一些民乐合奏。现在古筝合奏的形式多样,有和民乐合奏的《枉凝眉》还有和钢琴合奏的《临安遗恨》等等,在演奏形式上取得了重大突破。由于其丰富的音色和演奏技巧,所以有了很多不同的演奏形式。在独奏和合奏方面不仅继承了传统还取得了新的成就,弹唱因为难度希望在将来有进一步的发展。
(17)

(18)

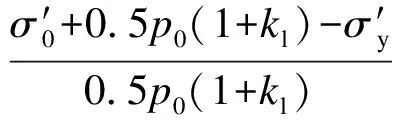

(19)


(20)
按沉降变形计算地基的平均固结度Us为

(21)
根据文献[6,13-14]可知,t时刻土体沉降St及最终沉降S∞的计算公式如下:
正常固结土
(22)

(23)

(24)

(25)


(26)

(27)

2 实例验证


表1 不同方法计算得到的最终沉降量 mm
由表1可知,利用不同方法计算的最终沉降量基本相近,且本文解答的计算结果与实测值最为接近,与Indraratna解[5]、Tuan解[10]及Hansbo解[12]的差别在5%以内;Tuan解[10]相对于Hansbo解[12]的沉降量偏小.
利用不同方法计算得到的超静孔隙水压力以及任意时刻的沉降量分别见图2和图3.由图2可知,固结初期基于不同解答所得的超静孔压与实测数据都有不同程度的偏差,整体来说都是偏小的.随着时间的增长,考虑固结过程土体参数变化的解答与超静孔隙水压力实测曲线吻合,基于Indraratna解[5]、周琦解[6]所得的结果略大于实测值.由图3可知,不考虑非线性时,基于Tuan解[10]及Hansbo解[12]计算得到的沉降明显小于实测值及其他计算值,尤其是在固结初期,这种差别较为显著.周琦解[6]由于仅考虑了正常固结状态时的沉降,因此其沉降计算值明显小于实测值.基于Indraratna解[5]及本文解答所得的结果与实测值较为吻合.由此可见,基于本文解答的计算结果更加接近实测结果.

图2 超静孔隙水压力
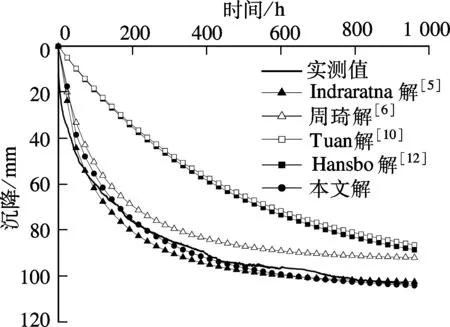
图3 不同时刻的沉降量分布
3 固结性状影响因素分析







图5 /对固结度的影响
4 结语
本文考虑真空荷载沿深度衰减分布的实际边界条件,引入能对土体压缩曲线线性化的双对数坐标lg(1+e)-lgσ′,建立了真空预压砂井地基非线性固结近似解答,计算得到的沉降、超静孔压与实测值很接近.通过参数计算分析可知,对于超固结土而言,根据变形计算的固结度随着压缩指数与渗透指数比值的增大而减小,随着真空度沿深度衰减系数的减小而减小;当压缩指数与渗透指数比值大于1时,正常固结状态中基于孔压计算的固结度随真空荷载衰减系数的减小而增大.随着压缩指数与回弹指数比值的增大,地基超静孔压消散速率逐渐增大,超固结状态下的沉降速率逐渐减小,正常固结状态下的沉降速率逐渐增大,土体由超固结状态进入正常固结状态的时间逐渐增加.
)
[1] 龚晓南. 地基处理手册[M]. 3版.北京:中国建筑工业出版社,2008.
[2] 赵维炳. 控制工后沉降处理深厚软土地基[M]. 北京:人民交通出版社,2006.
[3] Schiffman R L, Fungaroli A A. Consolidation due to tangential loads[C]//Proceedingsofthe6thInternationalConferenceonSoilMechanicsandFoundationEngineering. Montreal, Canada, 1965: 188-192.
[4] Hansbo S, Jamiolkowski M, Kok L. Consolidation by vertical drains[J].Géotechnique, 1981,31(1): 45-46.
[5] Indraratna B, Rujikiatkamjorn C, Sathananthan L. Radial consolidation of clay using compressibility indices and varying horizontal permeability[J].CanadianGeotechnicalJournal, 2005,42(1): 330-341.
[6] 周琦,刘汉龙,陈志波. 考虑固结参数变化时砂井地基的非线性径向固结[J].岩土力学,2007,28(S1):855-858.
Zhou Qi, Liu Hanlong, Chen Zhibo. Non-linear radial consolidation of sand-drained ground with varying volume compressibility and horizontal permeability[J].RockandSoilMechanics, 2007,28(S1): 855-858. (in Chinese)
[7] 董志良. 堆载及真空预压砂井地基固结解析理论[J]. 水运工程,1992(9):1-7.
Dong Zhiliang. Consolidation theory on heaped load and vacuum preloading of sand drain foundation[J].PortandWaterEngineering, 1992 (9): 1-7. (in Chinese)
[8] Indraratna B, Rujikiatkamjorn C, Sathananthan L. Analytical and numerical solutions for a single vertical drain including the effects of vacuum preloading[J].CanadianGeotechnicalJournal, 2005,42(4):994-1014.
[9] 彭劼,董江平,宋恩润,等. 考虑加载过程的真空预压轴对称解析解[J]. 岩土力学,2010,31(S1):79-85.
Peng Jie, Dong Jiangping, Song Enrun,et al. Axisymmetric analytical solution of vacuum preload considering the loading process[J].RockandSoilMechanics, 2010,31(S1):79-85. (in Chinese)
[10] Tuan A T, Toshiyuki M. Equivalent plane strain modeling of vertical drains in soft ground under embankment combined with vacuum preloading[J].ComputersandGeotechnics, 2008,35(5): 655-672.
[11] 张仪萍,严露,俞亚南,等. 真空预压加固软土地基变形与固结计算研究[J]. 岩土力学,2011,32(S1):150-154.
Zhang Yiping, Yan Lu, Yu Yanan,et al. Solutions for settlement and consolidation of soft ground with vacuum preloading[J].RockandSoilMechanics, 2011,32(S1):150-154. (in Chinese)
[12] Hansbo S. Consolidation of fine-grained soils by prefabricated drains[C]//Proceedingsofthe10thInternationalConferenceonSoilMechanicsandFoundationEngineering. Stockholm, Sweden, 1981: 677-682.
[13] Butterfield R. A natural compression law for soils [J].Géotechnique, 1979,29(4): 469-480.
[14] 刘维正. 饱和粘性土原位力学特性分析与应用研究[D]. 南京:东南大学交通学院,2011.
[15] 韩文君. 劈裂真空法加固软土地基理论与工程应用研究 [D]. 南京:东南大学交通学院,2012.

