固体燃料冲压发动机燃速预示模型及其特性

谢爱元，武晓松，王向东

（1.南京理工大学 机械工程学院，南京210094；2.晋西工业集团有限责任公司，太原030027）

固体燃料冲压发动机（Solid Fuel Ramjet，SFRJ）的燃面退移速率（简称燃速）不仅与固体燃料、来流空气质量流率、总温有关，还和燃烧室结构尺寸等息息相关[1－4]。目前国内外的科研工作者通过大量的实验研究，拟合出单一因素下的燃速公式[1－4]，成本高昂。同时，试验表明，在其它条件均相似的情况下，尺寸越小的固体燃料冲压发动机具有更高的燃面退移速率，且差别较大[2－3]；即针对某一尺寸发动机所得的实验结果，不能用于与其几何相似的另一尺寸发动机的工程设计中。由此可见，建立能够对不同尺寸、来流条件下固体燃料冲压发动机燃速进行准确预示的模型显得尤为重要。

假定工作过程中固体燃料通道内腔的表面温度（以下简称为内表面温度）为装药的液化温度，且不变；流场中不存在回流区。在上述简化的基础上，文献[5]建立了固体燃料冲压发动机的燃速模型。由于其简化得太多，导致其预示的结果误差很大，在来流空气总温Ta＜450K的工况中，误差超过30%。

本文在文献[5]的基础上，采用回流区内平均燃速公式，结合控制固体燃料燃速的阿雷尼乌斯公式来修正燃料内表面温度。建立了固体燃料冲压发动机燃速模型，编写燃面预示程序，进行了燃速计算并与已有实验进行对比，验证了该方法的准确性；首次通过数值计算发现工作过程中固体燃料内腔体积随时间呈线性关系变化并做了理论分析。

1 燃速模型

固体燃料冲压发动机的物理模型如图1所示。

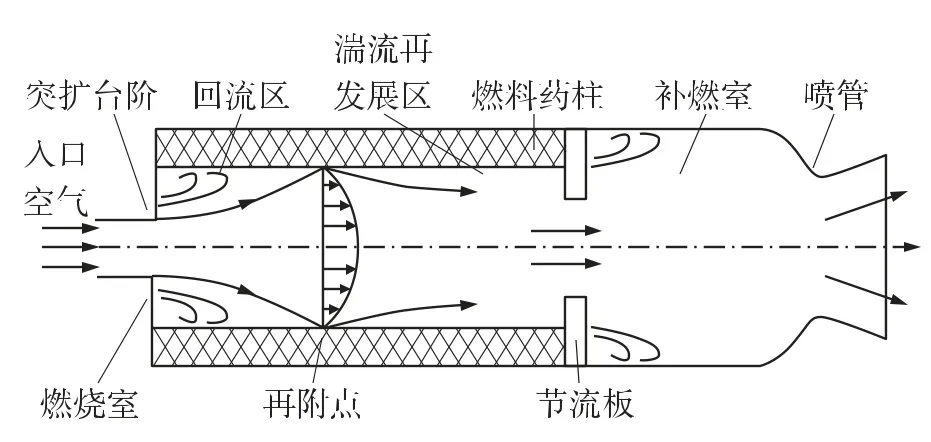
图1 固体燃料冲压发动机燃烧室流场示意图

实验研究表明，在低压下，固体燃料冲压发动机中流场与固体装药表面间的辐射换热量占总换热量不足5%。忽略辐射，在燃料表面上，存在能量平衡：

式中：h为对流换热系数，Tf为火焰温度，Ts为燃料表面温度，ρf为固体燃料密度，为局部燃速，hv为单位质量固体燃料的有效汽化热。

基于湍流边界层传热理论对对流换热系数进行求解，文献[5]建立了固体燃料冲压发动机平均燃速计算公式：

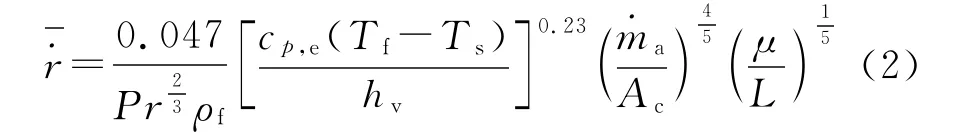
如图1所示，由于突扩台阶的作用，固体燃料冲压发动机燃烧室内流场存在流动的分离与再附着，以再附着点为界可将流场分为2个区域：燃烧室入口至再附着点为回流区，该区域内涡旋流动为主要流动；再附着点以后为湍流再发展区，该区域内湍流附面层不断增厚；回流区与湍流再发展区的换热量不能按同一种方法计算。式（2）是基于湍流边界层传热理论而得的，故只能用于湍流再发展区的燃速计算，而不适用于回流区。

式中：Lr为回流区长度。

由此可见，当其他参数不变时，再发展区中，平均退移速率正比于（Ld＝L－Lr，为再发展区长度）。

回流区内燃速的平均值可表示为[6]

式中：a为与燃气粘性、燃料汽化热有关的比例系数；Ta为来流空气总温；Dp，Din分别为装药通道直径及燃烧室入口直径。

试验研究发现，Lr与燃烧室入口台阶高度H（H＝（Dp－Din）/2）有关，无量纲化后的回流区长度为

至此，燃烧室内固体燃料瞬时平均燃速可表示为

对于给定的氧化剂/燃料混合物，其燃烧状态的影响因素有：环境压力，氧化剂/燃料的质量比，氧化剂/燃料的初温等。而最大的影响因素为氧化剂/燃料的质量比：

式中：MR为空燃比，Ab为燃料的燃面面积。且有

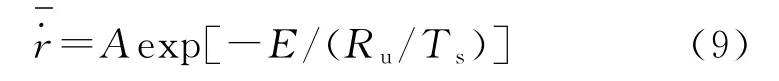
式中：A，E分别为燃料退移的前指因子、活化能；Ru为通用气体常数。

至此，假定固体燃料壁面温度Ts，联立方程（3）～方程（8）便可求出燃速，将其代入方程（9）中，反解出对应的壁面温度，判断收敛性。未收敛则修正壁面温度，再次求解；收敛则更新相关参数，进入下一个时间步求解。

同时，对于固体燃料燃速，存在关系式：

2 燃速计算

本文假设 Polymethy/methacrylate（PMMA）、Polyethylene（PE）的热解产物分别为单体 MMA（C5H8O2）[1]和 C2H4。

2.1 影响燃速的参数选取及计算流程

国内外大量文献表明，固体药柱的燃速受药柱通道直径，燃烧室入口直径，燃烧室压力，来流空气质量流率、总温等因素影响。国内外研究结果表明，在低压下（燃烧室压力pc＜0.8MPa），燃烧室压力变化对燃 速 的 影 响 很 小[1，4]；本 文 所 计 算 的 工 况 均在0.8MPa以下，因此仅考虑药柱通道直径，燃烧室入口直径，来流空气质量流率、总温对燃速的影响。

计算中取PE的有效汽化热、密度、前指因子及活化能分别为5.5 MJ/kg[2]，965kg/m3[8]，640 m/s和133.66kJ/mol[9]；PMMA 的有效汽化热、密度、前指因子及活化能分别为2.0 MJ/kg，1 180kg/m3[8]，0.072 1m/s和53.086kJ/mol[9]。固体燃料冲压发动机中常用由温升定义的燃烧效率ηΔT来表征固体燃料的燃烧效率。成功点燃的固态碳氢燃料，ηΔT平均值约为0.9[1，4]，本文取该值作为 PMMA、PE的燃烧效率。计算步长为0.005～0.05s。收敛准则为：固体燃料质量消耗率的初判值与二次判断值的相对误差小于0.5%，且壁面温度相对误差小于1%。

2.2 计算结果与分析

本文对PE、PMMA为燃料的固体燃料冲压发动机燃速共进行了34次计算，结果如表1所示。表中试验数据的来源为燃速公式一栏中所对应的参考文献，燃速公式为国外进行单一因素试验所得结果为实验所得的平均燃速为本文计算所得的平均燃速，Dp0为装药初始内径，Δ为误差。其中，文献[3]拟合的公式，燃速与压力pc有关，计算其退移速率的试验值时，取pc＝0.7MPa（本文计算产物物性时选取的压力）。

表1 计算结果

由表1可知计算值与实验值的误差在－14.4%～13.5%之间；当燃料为PE时，误差绝对值的平均值为4.94%；燃料为PMMA时，误差绝对值的平均值为8.89%。

由1＃～4＃，9＃的结果可知，燃速随着来流空气总温增大而增大。这是因为随着来流空气总温增大，燃烧产物的温度将变高，流场与固体装药间的换热量增大，使得燃速增大。

由5＃，6＃，10＃的结果可知，燃速随着来流空气质量流率的增大而增大。来流空气质量流率的增加，使得发动机内流动速度增大，对流换热系数变大，导致燃速变大。

由7＃，8＃的结果可知，燃速随着入口直径的减小而增大。来流空气质量流率相同时，入口直径越小，燃烧室内主流区的雷诺数、努赛尔数、对流换热量越大[10]，使得燃速变大。

对比9＃和10＃，来流空气总温均为300K的条件下，9＃的装药内径大于10＃，来流空气质量流率、突扩台阶高度的相对量均大于10＃中的3个工况，燃速小于10＃的3个工况，说明燃速随着装药内径的增大而减小。内径的增大使得装药通道内的流动速度降低，对流换热系数减小。

以上结论均和已有试验结果相符，证明了本文所建立的燃速计算模型是准确可靠的。

图2为工作过程中药柱内腔体积V随时间变化的对比图，其中试验数据取自文献[7]。

图2 燃料内腔的瞬时体积

通过线性拟合发现，34次计算所得的药柱内腔瞬时体积V均为

式中：b，c为系数；t为时间。

采用上述标准，所得结果的相关性最小值为0.998 4。这表明，工作过程中燃料的质量消耗率、空燃比不变，由此得出，火焰温度不变，产物的物性不变。

由式（10）可得：

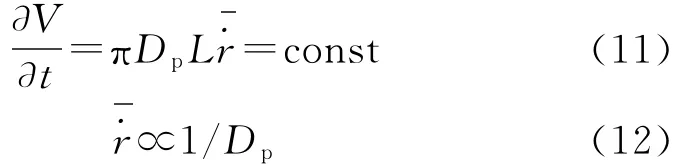
为解释这一现象，本文做如下假设：①工作过程中火焰温度及产物的物性不变，由文献[11]的试验可得，工作过程中燃料质量消耗率、空燃比不变，同时来流空气总温不变，在此前提下进行这一假设是合理的；②忽略工作过程中燃料壁面温度的微小变化，以图3中2个工况为例，计算结果表明，工作过程中壁面温度变化值/平均值分别为80 K/1 250K，100 K/1 380K；③不考虑再附着点的移动，图3中a＝8.5g/s工况试验过程中，再附着点位置仅变化8mm/70 mm（再附着点位置变化量/药柱长度）；④不考虑燃料壁面质量加入引起同一时刻不同截面质量通量的变化，工作过程中，与来流空气相比，固体燃料的质量流率较低，约在5%～8%之间。

Heaton等人的研究结果表明，管内流动入口区不同轴向位置的Nu仅与Pr及无量纲特征长度x/（DReDPr）相关[11]，其中，D为圆管内径，ReD为按内径所定义的雷诺数。如图3所示，本文涉及的问题对应于图中的混合入口段问题，解依赖于x/（DReDPr）和Pr，图中仅给出了Pr＝0.7的解。

图3 圆管内流入口段努赛尔数的解[11]

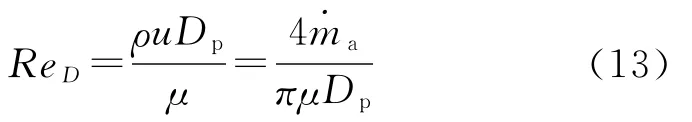
式中：u为流速。

由图3可得，装药通道再发展区内努赛尔数Nu可表示为2个函数的乘积：

由假设④可得：

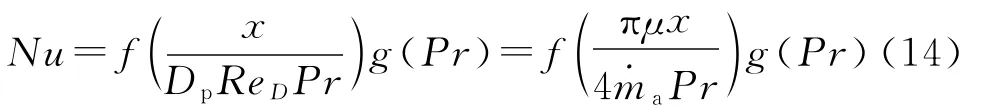
由方程（1）可得再发展区内不同点的燃速：

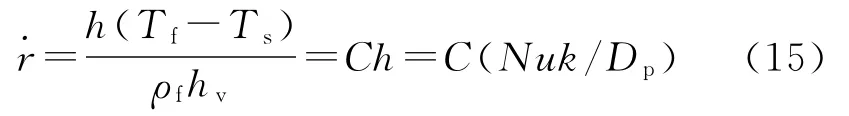
式中：C＝（Tf－Ts）/（ρfhv），k为导热系数。

由假设①②得，工作过程中，式（15）中C为常数。

结合假设①及式（14）、式（15）可得，工作过程中再发展区内各点的燃速与内径Dp成反比，故有

至此，式（10）～式（12）所对应的现象得到了解释。

表2为同一工况下不同装药长度的燃速计算结果。对其进行指数拟合，结果为

这与式（12）理论推导的结论相符，造成差别的原因为：当只改变装药长度时，回流区长度Lr不变，导致再发展区长度Ld的相对增加量大于装药长度L的相对增加量，平均燃速减小量比L－0.2稍大。由此可见，长度对燃速的影响不可忽略。

3 结论

本文建立了固体燃料冲压发动机的燃速预示模型。编写了燃速预示程序，以PE、PMMA为固体燃料进行了34次的计算验证，主要结论如下：

①取燃烧效率ηΔT＝0.9，计算值与试验值吻合很好，误差在±15%以内，误差绝对值的平均值为5.87%；

②固体燃料的燃面退移速率随来流空气总温、质量流率、突扩台阶高度增大而增大，随通道内径增大而减小，这些结论与国内外实验相同；

③34次计算均表明，工作过程中固体燃料内腔体积随时间呈线性关系，这是继文献[7]的实验之后首次通过数值计算发现这一现象，并对形成此现象的原因做了分析；

④在给定工况下的计算结果表明，固体燃料冲压发动机中燃速正比于L－0.21，这是首个将工作过程中突扩台阶高度、再发展区长度变化考虑在内的固体燃料冲压发动机燃速模型。

[1]夏强.固体燃料冲压发动机工作过程研究[D].南京：南京理工大学，2011：81－108.XIA Qiang.Investigation on the working process of solid fuel ramjet[D].Nanjing：Nanjing University of Science and Technology，2011：81－108.（in Chinese）

[2]ELANDS P J M，KORTING P A O G.Combustion of polyethylene in a solid fuel ramjet：a comparison of computational and experimental result，AIAA88－3043[R].1988.

[3]SCHULTE G.Fuel regression and flame stabilization studies of solid fuel ramjets[J].Journal of Propulsion and Power，1986，2（4）：301－304.

[4]KORTING P A O G，GELD C W M.Combustion of PMMA in a solid fuel ramjet，AIAA86－1401[R].1986.

[5]谢爱元，武晓松，夏强.基于焓平衡法的固体燃料冲压发动机燃面退移速率模型[J].固体火箭技术，2012，35（5）：613－618.XIE Ai－yuan，WU Xiao－song，XIA Qiang.Prediction model of propellant regression in SFRJ based on enthalpy－balance[J].Journal of Solid Rocket Technology，2012，35（5）：613－618.（in Chinese）

[6]KRISHNAN S，GEORGE P.Solid fuel ramjet combustor design[J].Aerospace Science，1998，34（4）：219－256.

[7]ZVULONI R，GANY A，LEVY Y.Geometric effects on the combustion in solid fuel ramjets[J].Journal of Propulsion and Power，1989，1（5）：32－37.

[8]TIMNAT Y M，KORTING P A O G.Hybrid rocket motor experiments[R].Delft：Department of Aerospace Engineering，Delft University of Technology，1985.

[9]WILDE J P D.Fuel pyrolysis effects on hybrid rocket and solid fuel ramjet combustor performance[M].Delft：Delft University Press，1991：68－78.

[10]NETZER A，GANY A.Burning and flame holding characteristics of a miniature solid fuel ramjet combustor[J].Journal of Propulsion and Power，1991，7（3）：357－363.

[11]INCROPERA F P，DEWITT D P.传热和传质基本原理[M].葛新石，叶宏译.北京：化学工业出版社，2009：317.INCROPERA F P，DEWITT D P，BERGMAN T L，et al.Fundamentals of heat and mass tranfer[M].Beijing：Chemical Industry Press，2009：317.（in Chinese）