贝叶斯估计动态汽车衡分时段数据融合研究



贝叶斯估计动态汽车衡分时段数据融合研究

李丽宏，徐文举

（太原理工大学信息工程学院，山西太原030024）

摘要：数据融合是一个多级、多层面的数据处理过程，主要完成对来自多个信息源的数据进行自动检测、关联、相关、估计及组合等处理。该文通过分析动态汽车衡的称重原理，对两路称重传感器不同时段的输出数据进行分析，提出基于贝叶斯估计的数据融合方法。实验检定表明：采用这种融合方法的动态汽车衡称重误差小，克服了动态汽车衡由于车辆振动、路面不平和传感器灵敏度分散性、传感器线性度误差等因素对称量结果的影响，准确度高。

关键词：数据融合；动态汽车衡；贝叶斯估计；自动检测

0　引　言

动态汽车衡由于其称量节省时间、效率高等优点，目前已经广泛应用于高速公路计重收费系统和超限检测系统。然而，由于车辆振动和路面不平等因素使称重传感器的信号输出掺杂了复杂的干扰因素，使得动态汽车衡的精度无法保障[1]。因此，如何去除这些干扰因素成为动态汽车衡称重的技术难题。

本文通过对动态汽车衡两路称重传感器不同时段的输出数据进行分析[2]，采用贝叶斯估计的数据融合方法，对单次测量的结果分时段，得到相应的最佳融合数和置信距离矩阵，再通过贝叶斯估计的融合计算方法得到测量值的最终融合结果[3]。

1　基于贝叶斯估计的动态汽车衡分时段数据融合方法

本文提出的方法主要用于解决来自两路称重传感器分时段数据融合的问题，数据处理的目的是获得对称重数据更为可靠的估计。其两路传感器信号输出及各部分标注如图1所示。1为第一路称重传感器输出，2为第二路称重传感器输出，3为两路传感器的和，4为有效数据称量段所有数据的平均值，5为所测车辆的静态轴重测量值。根据此滤波后的波形，找到第一路传感器的最大值和第二路传感器的最大值，将这两点之间的数据作为有效称量数据，对这些数据的和求平均值，再根据相应的称量系数得到车辆实际的轮轴重量值[4-5]。

该算法原理分为置信距离理论、最佳融合数的选择方法、基于贝叶斯估计的融合计算方法3个部分[6]。

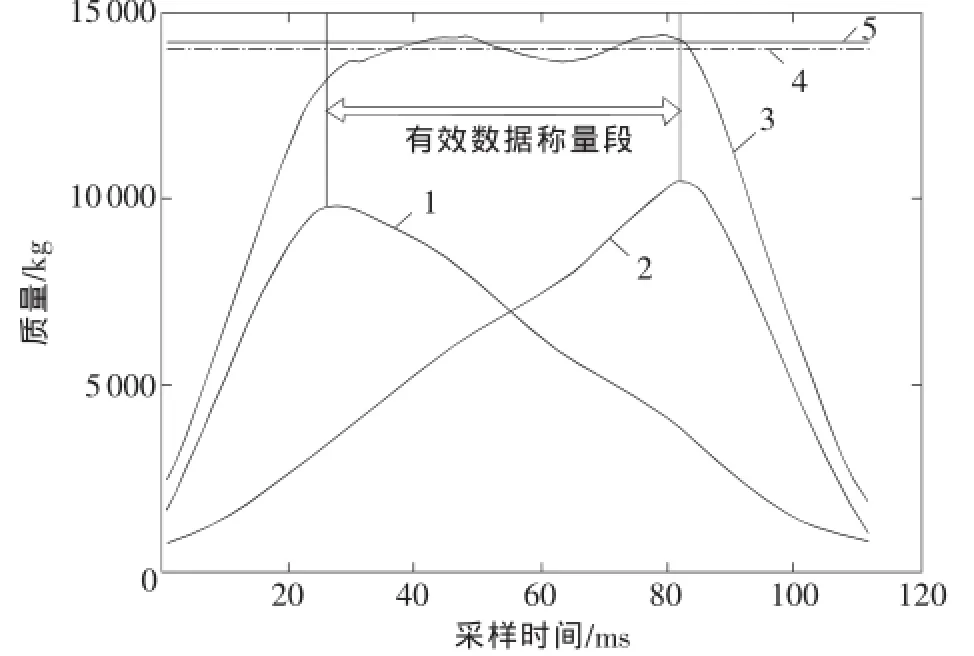
图1　动态汽车衡两路传感器数据输出

图2　数据输出分析

1.1置信距离

为了对称重传感器输出数据进行选择，必须对其可靠性进行估计。由于被测量的称重数据真值是未知的，因此对两路称重传感器不同时段的数据之间的关系进行判断。为了充分利用不同时段称量数据的先验知识，该方法根据其统计特性应用了置信距离的概念。

在动态汽车衡称重系统中，利用两路称重传感器对重量参数进行测量。两路输出数据之和服从高斯分布，将输出数据之和按时序分为n个数据段，Xi表示第i个时间段的输出数据。假设各个数据段同样服从高斯分布，将每个数据段单独看作一个数据源，同时看作对称量结果的n个贝叶斯估计，如图2所示。用pi（x）表示Xi的概率密度函数，xi和xj分别表示在一次测量中第i个和第j个时间段的输出数据，即xi和xj分别为Xi和Xj的一个样本。可得到：

式（1）中dij为xi对xj的置信距离，式（2）中dji为xj对xi的置信距离。由于Xi和Xj均服从高斯分布，可得到式（1）和式（2）中：

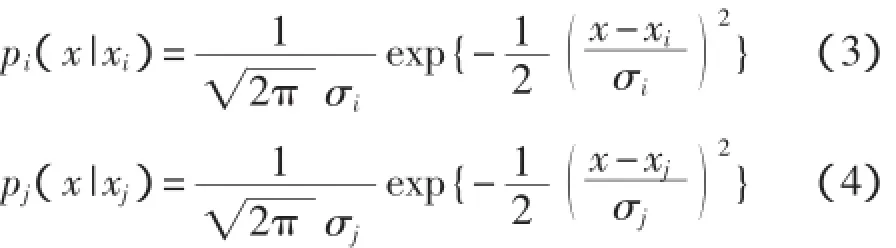
由上述可知，置信距离能够反映称重传感器不同时段输出数据之间的相互支持关系，如dij反映了i时段的输出数据对j时段的输出数据的支持程度，同样dji反映了j时段的输出数据对i时段的输出数据的支持程度。dij的值可借助于误差函数erf（θ）直接求得。误差函数为

据文献[7] 和文献[8] 知：

两种特殊情况，当xi=xj时，dij=dji=0；当xi>>xj或者xj>>xi时，dij=dji=1。

根据此方法可以得到两路称重传感器中任意两个时段输出数据之间的置信距离，把这些值用矩阵的形式表示出来，即为不同时段输出数据的置信距离矩阵。

1.2最佳融合数的选择

通过上面的分析得到置信距离矩阵，然后需要选择一个临界值对置信距离进行划分，借此判断不同时段输出数据之间是否支持。现以αi表示dij的临界值，即当dij≥αi时认为第i个时间段的输出不支持第j个时间段的输出数据，而当dij≤αi时认为第i个时间段的输出支持第j个时间段的输出数据。在此定义一个二值变量βij表示第i个时间段是否支持第j个时间段的输出数据，即：

由此得到一个关系矩阵[9]：

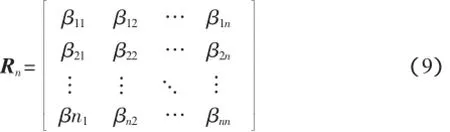
此关系矩阵表示任意两个时间段输出之间是否支持，由此可以判断每个时间段输出数据是否被认为有效。因此需要选择另一个临界值n，即对于某一个时间段数据输出，当它被多于n个时间段数据输出支持时认为其输出数据有效。由此依据关系矩阵对各个时间段的输出结果进行判断，得到m个有效数据参与融合计算，而m个有效数据成为最佳融合数。

1.3基于贝叶斯估计的融合计算方法

贝叶斯估计充分利用了先验知识，把每一次的检验过程动态看作对先验知识的不断修正。本文n个数据段中，最佳融合数位为m（m≤n）。贝叶斯公式为

为后续数据融合需要，将关系矩阵选择的m个最佳融合集合表示为（x1，x2，…，xm）[10]。得到一组数据后，被测参数的条件概率密度函数可由式（11）表示：

若μ和Xk均服从高斯分布，即μ～（μ0，σ02），Xk～（μ，σk2），在这里令ω=p（

x，x

1

，…，x），可知ω是

12m与μ无关的常数。由此可得：

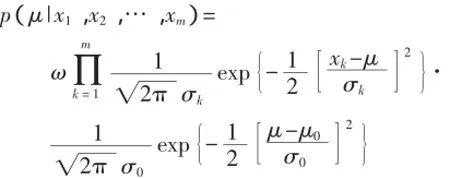
化简后得到：

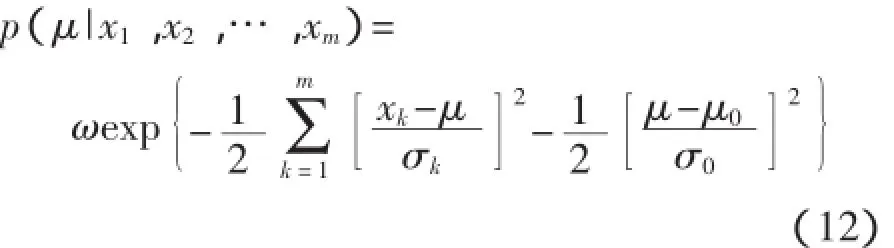
式（12）中的指数部分是关于μ的二次函数，故p（μ|x1，x2，…，xm）仍然服从高斯分布，设其服从N（μN，σN2），即：

因此，μ′即为μ的最优融合数据。

2　数据融合示例

测得的一组质量数据，设其服从高斯分布，g～N（14003.96，59220.11）。实验采用了两轴货车加载砝码，在静态情况称得汽车前轴重量是5 193 kg，后轴重量是14 175 kg，本实例采用后轴，其测量误差为1.21%。将这组数据按时序分为n=7段，假设各自服从高斯分布，获得数据如表1所示。

表1　分时段后的数据

根据表1和本文论述的方法得出相应的置信距离矩阵：

D

取dij的界线值为1，得到关系矩阵R：

取至少被另外6个时序段所支持的测量数据为有效数据，由R可知，最佳融合数m=2，融合集为{x2，x3}，由式（14）可得出最终的融合结果：

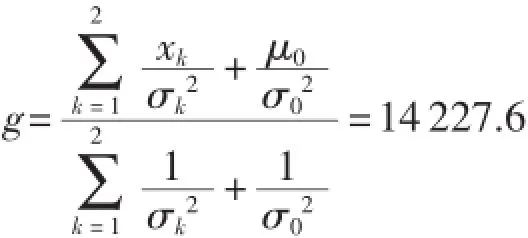
融合后的误差为0.37%，多次测量结果如表2所示。

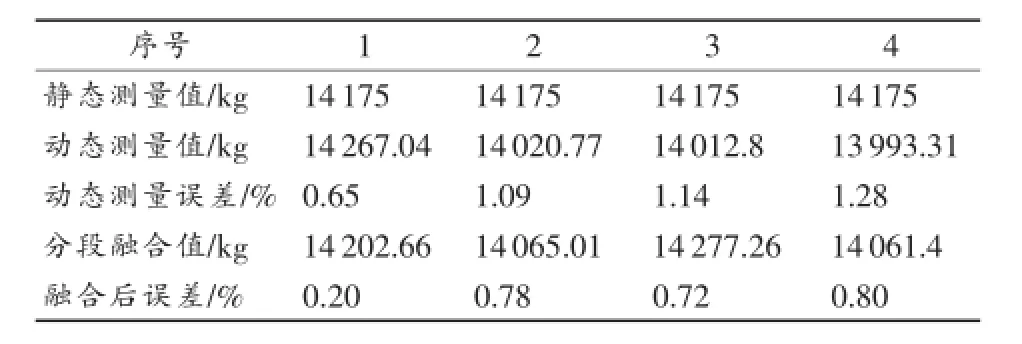
表2　多次测量结果

由以上仿真结果可以看出，对称重数据进行贝叶斯估计后可以得到更加精确的称重数据，选择好最佳融合数，然后利用得到的置信距离矩阵进行贝叶斯估计可以很容易得到融合后的称重数据。通过表2可以看出，贝叶斯估计的数据融合方法能够使动态汽车衡的准确度更高。

3　结束语

实践证明，这种融合方法方便简单，减小了机动车通过秤时由于路面、秤体自身的振动及在加减速时的负荷变动等形成的动态振荡会引入的称重误差，准确度有了大幅提高。

参考文献

[1] 裴春清．基于深度滤波的动态汽车衡算法[J] .科技应用，2008，37（S0）：7-9.

[2] 徐进．车辆动态称重仪表的设计[D] ．太原：太原理工大学，2010．

[3] Klein L A.多传感器数据融合理论及应用[M] .2版.戴亚平，等译．北京：北京理工大学出版社，2004．

[4] 韩旖旎．基于过采样技术的动态汽车称重仪的设计[D] ．太原：太原理工大学，2010．

[5] 马海平，李晓林.新型动态汽车衡称重系统的设计与实现[J] .中国测试技术，2007，33（1）：18-19，73.

[6] 吴小俊．基于Bayes估计的多传感器数据融合方法研究[J] .系统工程理论与实践，2000（7）：45-48．

[7] 陈福增．多传感器数据融合的数学方法[J] .数学的认识与实践，1995（2）：11-15．

[8] 阮沈勇．Matlab程序设计[M] .北京：北京航空航天大学出版社，2006．

[9] 禹春来，许化龙，黄世奇.基于关系矩阵的多传感器数据融合方法[J] .航空计算技术，2005（1）：23-26．

[10] 中山大学数学力学系．概率论及数理统计[M] ．北京：高等教育出版社，1980．

Multi-period data fusion research of dynamic vehicle weighbridge based on Bayesian estimation

LI Li-hong，XU Wen-ju

（College of Information Engineering，Taiyuan University of Technology，Taiyuan 030024，China）

Abstract:Data fusion is a multi-level and multi-layered data process，whose main function is to detect，correlate，relate，estimate and assemble the data of multiple sources automatically. Based on the principle of dynamic vehicle weighbridge，the paper analyzed the output data of two road weighing sensors at different times，and proposed a theory of data fusion method based on Bayesian estimation. The experimental verification shows that the dynamic vehicle weighbridge error is small by using this method. It overcomes the dynamic truck scale caused by vehicle vibration，road surface roughness，the sensitivity of the sensor，the sensor dispersion linearity error and other factors on the weighing results with high accuracy.

Key words:data fusion；dynamic vehicle weighbridge；Bayesian estimation；auto detect

收稿日期：2013-03-12；收到修改稿日期：2013-05-10

doi：10.11857/j.issn.1674-5124.2013.05.029

文章编号：1674-5124（2013）05-0107-03

文献标志码：A

中图分类号：U492.3+21；TP212.1+2；TP274；O212.8

作者简介：李丽宏（1963-），男，山西晋城市人，副教授，研究领域为控制理论与控制工程，检测技术与智能仪表。