中小河道突发事故污染源强非稳态过程反问题

金文龙，彭 辉，高俊杰，潘曼曼，韩龙喜

(1.河海大学环境学院，江苏南京 210098;2.水利部水文局，北京 100053)

随着我国社会经济的迅速发展，突发性水污染事故频频发生，由于突发水污染事故的不确定性及发现时间的滞后性，一般情况下很难及时监测到完整的污染源排放历史，给事故发生后的预警预报与处置工作带来困难。因此，如何在突发性水污染事故发生后，根据下游污染物浓度分布等信息反演完整的污染源排放历史具有重要意义。

在环境水力学反问题领域，地表水污染源的反演问题通常被提为源项识别反问题，其主要任务是根据环境水力学测量数据，来反推污染源的信息，如污染源的强度和位置等。目前相关方面的研究尚不成熟，Akcelika 等［1］采用变分有限元方法求解了对流扩散输运的源项反演问题;Wang 等［2］提出了多孔介质流动中的源项识别的马尔科夫随机场模型;Ling 等［3］从理论上研究了二维对流扩散方程的源项位置识别问题;闵涛等［4］将对流-扩散方程源项识别反问题转化为优化问题，并用遗传算法求解;韩龙喜［5］以污水处理费用最小为目标函数，采用遗传算法求解了一维水质模拟带约束条件的污染物排放量控制反问题;并构造了河网地区带约束条件的污染源控制反问题［6］，并采用约束最优化算法中的简约梯度法成功求解。王泽文等［7］研究了流域中单个点污染源识别问题的唯一性、稳定性和反演算法。

地表水污染源的反演问题也可被提为边界条件反问题，金忠青等［8］分别应用脉冲谱- 优化法和Green 函数法求解了一维、二维对流-扩散方程边界条件控制反问题，基本解决了恒定水体中上游污染控制问题;韩龙喜等［9］首次给出水网地区无约束的水质边界浓度反问题的提法，并采用局部基本解展开算法进行稳态条件下边界浓度反演;李子［10］将识别突发性污染源以及模拟污染物浓度时空变化过程提为边界条件控制反问题，并对以GST-MQ(global space time-multi quadric)配点法为基础的反演方法进行了研究。

总体而言，关于污染源反演问题的研究主要集中在污染源排放位置或排放区域已知情况下的排污(污染源)的控制问题以及对边界上浓度变化过程的反演，很少涉及直接对污染源源强变化过程的反演。因此，笔者在污染源位置已知的情况下，根据事故下游某断面一组污染物浓度的时间序列观测资料，提出了中小型河道一维突发性水污染事故源强变化过程的反问题。在反问题的求解方法上，笔者运用了径向基配点法，该方法作为一种新兴的无网格方法具有不依赖于控制方程的形式、multi-quadric(MQ)函数的插值精度高、求解反问题与正问题计算过程相同、不需要迭代优化过程以及对测量数据有较强的适应性等独特优势。

1 问题的数学描述

1.1 中小型河道一维水质模型

假定研究水域是长度为L 的中小型河道，污染源位于研究水域上边界(x =0)处，河道宽度和深度均远小于河段的长度，当污染事故发生时，污染物在对流、扩散过程的作用下在水域［0，L］内随水体迁移扩散，对于中小型河道，河段一般较为顺直，因此污染物的断面平均浓度C 沿河段的分布可用源项为零的一维对流-扩散方程来描述:

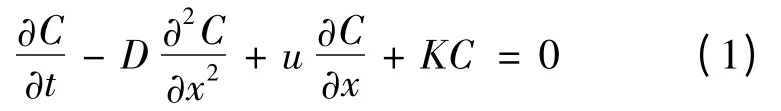
式中:D 为扩散系数;t 为时间;x 为空间坐标;u 为流速;K 为污染物降解系数。

其初始条件为:

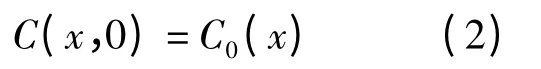
上边界条件用源强的变化过程S(t)来表示:

式中:Q 为流量;C0为上游边界(x =0)处的背景浓度。

下边界为Neumann 边界条件:

当D、u、K、C0(x)、C0、S(t)已知时，式(1)～(4)构成河流一维水质模拟分析的适定问题即正问题，可采用常规的计算方法预测水域中任何时刻的污染物浓度分布C(x，t)。为研究简便计，不妨构造一个污染源，根据突发性水污染事故的特点，假定污染源为分布于某一时段的非连续源，其源强变化过程的数学描述为:

其中H 为阶跃函数:

式中:As为源强排放峰值;Ts为排放的持续时间。

假定初始条件C0(x)=0，则定解问题式(1)～(4)的解析解为:

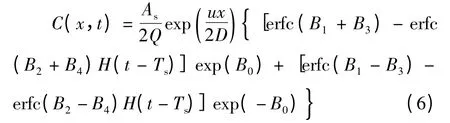
1.2 反问题的提法

由于突发水污染事故的不确定性，一般情况下很难及时监测到完整的源强变化过程S(t)，从而导致边界条件C(0，t)的缺失，对求解正问题造成困难。为初步判断污染源的真实情况，一类有效的方法就是在污染源下游某断面x =l 处设置观测点，通过采样观测，获得一组污染物浓度的时间序列观测资料:

式中，W 为观测数据的个数。

通过这组观测数据来反演源强的变化过程，这就构成了一类源强变化过程的反问题。这类反问题的实质是给出方程的部分解来确定控制方程的边界条件，根据环境水力学反问题的观点，即为边界条件控制反问题。应当指出的是，从物理角度出发，边界条件和污染源项是两个不同的概念，但在水质模型中，当污染源位于边界时边界条件反问题与源项反问题常是可以相互转换的，两者从数学角度看处理方法是一致的［11］。

2 反问题的求解方法

2.1 最小二乘GST-MQ 配点法简介

径向基函数配点法是求解偏微分方程的一种配点型无网格法，它的基本思想是把未知函数用一组径向基函数的线性组合来表示，然后再令域内的各节点满足控制方程，边界上各节点满足一致边界条件［12］。最小二乘-径向基函数配点法的基本思想是用径向基函数逼近未知函数后，令控制方程在包括区域内和边界上的所有节点上满足，而初始条件、边界条件等则在其各自相应的节点上满足，最后利用最小二乘法求解超定线性方程组［13-14］。相对于传统径向基配点法，最小二乘-径向基配点法可以松弛边界上各节点，满足边界条件这一要求，从而改善线性方程组中系数矩阵的病态条件，提高解的精度。

MQ 函数是由Hardy 于1968 年提出来的一种径向基函数［15］。对于一维空间，MQ 函数的形式为

式中:c 为形状参数;xk为空间基点坐标。

逆MQ 函数的形式为

由于MQ 函数和逆MQ 函数都只是空间距离的函数，只能用于求解稳态问题，而在水质模拟分析中，污染物的浓度变化是个非稳态的过程，因此引入全时空的概念，将时间维看作伪空间，进而将时间变量直接插入基函数形式中构造新的径向基函数。以逆MQ 函数为例进行构造，新构造的GST-MQ 径向基函数形式为:

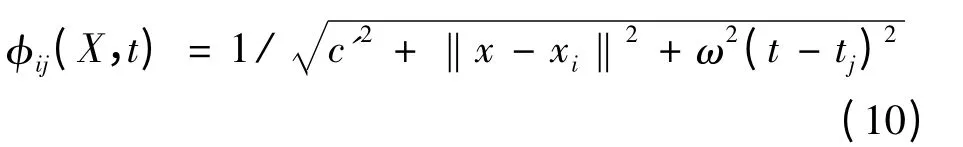
其中

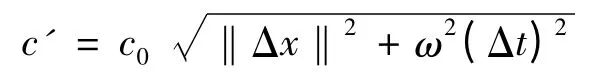
式中:ω 为引入的时空比例因子，以平衡时间和空间的属性差异;tk为基点时间;Δx 为空间上的配点距离;Δt 为时间上的配点距离;c0为形状参数相对值。

2.2 计算步骤

a. 将空间区域［0，L］和计算时间范围［0，T］分别用N 和M 个节点离散，则污染物浓度C(x，t)可由一组GST-MQ 径向基函数近似为:

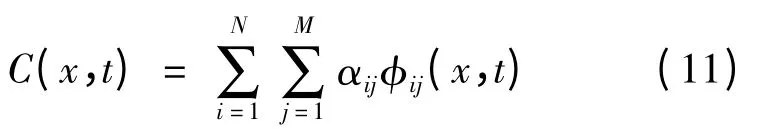
其中

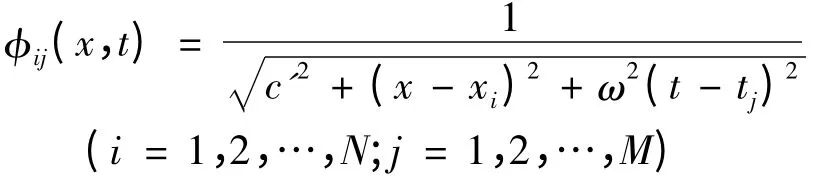
式中:αij为待定系数;N、M 分别为空间区域［0，L］和计算时间范围［0，L］上的配点总数。

b. 将式(11)代入式(1)，并在时空区域及边界上的所有节点上满足，可得一个关于αij、有N ×M个方程、N×M 个未知数的方程组:

c. 将式(11)代入式(2)，并在空间区域［0，L］的所有配点及t =0 上满足，可得一个关于αij、有N个方程、N×M 个未知数的方程组:

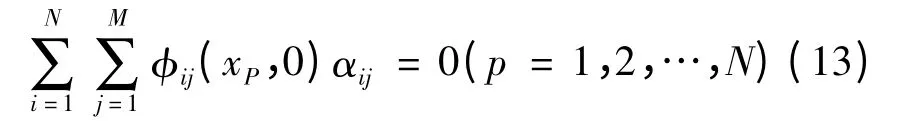
d. 将式(11)代入式(4)，并在x =L 及时间范围［0，T］的所有配点上满足，可得一个关于αij、有M个方程、N×M 个未知数的方程组:

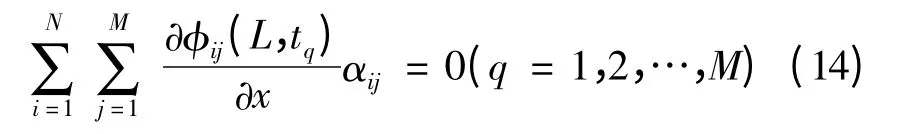
e. 将式(11)代入式(7)，并在x=l 及观测时间{tq;q=1，2，…，W}上满足，可得一个关于αij、有W个方程、N×M 个未知数的方程组:

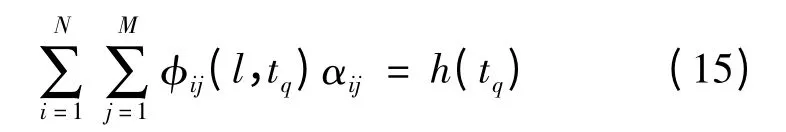
则式(10)～(13)构成了一个关于αij，含有N×M 个未知数，N×M +N +M +W 个方程的超定线性方程组，即最小二乘问题:min{‖Aα -b‖2}。用奇异值分解法解这个最小二乘问题可得系数αij，再利用式(3)可反演得源强变化过程S(t)。

3 数值算例

假定事故水域范围L =5 000 m，计算时间T =10000 s，水体流动速度u=0.5 m/s，流量Q=20 m3/s，扩散系数 D = 1.0 m2/s，污染物降解系数K=0.000 1s-1。假定源强峰值As=200 g/s，污染物排放时间Ts=5000s，观测断面位于l=1000m 处，观测起讫时间为事发后400 ～10000s 时间段，观测频次为每隔400 s 观测一次，对应的观测数据个数W=25 个。

首先由正问题的解析解式(6)给出一组观测数据的理论值，再由式(16)生成观测误差并附加到理论值，作为实际的观测数据值:

式中:h(tq)为构造的观测数据的实际值;h'(tq)为观测数据的理论值;e 为误差水平;ωq为一组符合标准正态分布的随机数。

用式(7)和式(16)分别计算观测数据的理论值h'(tq)和实际值h(tq)，误差水平e 取0.02，部分计算结果见表1。

表1 计算的观测数据理论值和实际值的部分结果

最小二乘GST-MQ 配点法的计算参数有:空间上的配点总数N、时间上的配点总数M、形状参数c0、和时空比例因子ω。对于空间和时间上的配点总数N、M，一般情况下，N 和M 越大，计算结果越精确，但计算机所需内存越多，计算时间越长，本文在计算时取N =51、M =26。对于形状参数c0和时空比例因子ω，反演误差对这两个参数的取值较为敏感，本文经试算分析，在计算时取c0=1.5，ω=1.4。

根据表1 中的观测数据的实际值，使用最小二乘GST-MQ 配点法程序对源强变化过程S(t)进行反演。另外，为减小计算结果的波动，提高反演精度，对源强增加约束条件，使源强不小于0，即S(t)≥0。经计算，反演计算结果与真实值的比较见图1。

由图1 可知:在t =0 s 和t =Ts=5 000 s 附近，S(t)的反演解与真实值偏差较大，这是由于t =0 s时刻污染源排放突然开始，t=5 000 s 时刻污染源排放突然停止造成的。在数学上，GST-MQ 径向基函数连续可导，因此用连续光滑的反演解描述真实排放过程在t=0 s 和t =5 000 s 处的间断性。在其他时段，S(t)的反演解在真实值附近波动，大致反映了污染源的排放过程。总体而言，S(t)的反演解在大多数时段比较接近污染源的真实情况，反演结果较为准确。

4 结 语

根据中小型河道特点以及突发性水污染事故的特征，用污染源下游某断面污染物浓度的时间序列观测资料作为附加条件，提出了突发性水污染事故污染源强变化过程反问题，并用最小二乘GST-MQ配点法对反问题进行了求解。数值算例表明，反问题的计算结果准确合理。

图1 S(t)的反演解和真实值比较

［1］AKCELIKA V，BIROS G，GHATTAS O，et al.A variational finite element method for source inversion for convectivediffusive transport［J］. Finite Elements in Analysis and Design，2003，39:683-705.

［2］WANG J，ZABARAS N. Using bayesian statistics in the estimation of heat source in radiation［J］. International Journal of Heat and Mass Transfer，2005，48:15-29.

［3］LING L，YAMAMOTO M，HON Y C，et al.Identification of source locations in two-dimensional heat equations ［J］.Inverse Problems，2006，22:1289-1305.

［4］闵涛，周孝德，张世梅，等.对流-扩散方程源项识别反问题的遗传算法［J］. 水动力学研究与进展:A 辑，2004，19 (4):520-524. (MIN Tao，ZHOU Xiaode，ZHANG Shimei，et al. Genetic algorithm to an inverse problem of source term identification for convectiondiffusion equation ［J ］.Chinese Journal of Hydrodynamics，2004，19(4):520-524. (in Chinese))

［5］韩龙喜.河道一维污染源控制反问题［J］.水科学进展，2001，12(1):39-44. (HAN Longxi. Inverse problem on amount of pollutant into natural channel［J］. Advances in Water Science，2001，12(1):39-44. (in Chinese))

［6］韩龙喜，朱党生.河网地区水环境规划中的污染源控制方法［J］. 水利学报，2001(10):28-31. (HAN Longxi，ZHU Dangsheng. The pollutant source control method for network water environment management ［J］. Journal of Hydraulic Engineering， 2001 (10 ): 28-31. (in Chinese))

［7］王泽文，邱淑芳. 一类流域点污染源识别的稳定性与数值模拟［J］. 水动力学研究与进展:A 辑，2008，23(4):364-371. (WANG Zewen，QIU Shufang. Stability and numerical simulation of pollution point source identification in a watershed ［J］. Chinese Journal of Hydrodynamics，2008，23(4):364-371. (in Chinese))

［8］金忠青，陈夕庆.用脉冲谱-优化法求解对流-扩散方程边界条件控制反问题［J］.河海大学学报:自然科学版，1991，19 (1):1-8. (JIN Zhongqing，CHEN Xiqing.Numerical solution to an inverse problem of boundary condition control for convection-diffusion equations by PST-Optimization ［J］. Journal of Hohai University:Natural Sciences，1991，19(1):1-8. (in Chinese))

［9］韩龙喜，蒋莉华，朱党生.组合单元水质模型中的边界条件及污染源项反问题［J］.河海大学学报:自然科学版，2001，29(5):23-26. (HAN Longxi，JIANG Lihua，ZHU Dangsheng. Inverse problem on boundary condition and pollutant source in water quality model of river network ［J］. Journal of Hohai University:Natural Sciences，2001，29(5):23-26. (in Chinese))

［10］李子.基于GST-MQ 配点法的突发水污染事故反演模型研究［D］.北京:清华大学，2010.

［11］刘晓东，姚琪，薛红琴，等.环境水力学反问题研究进展［J］. 水科学进展，2009，20 (6):885-890. (LIU Xiaodong，YAO Qi，XUE Hongqin，et al. Advance in inverse problems of environmental hydraulics ［J］.Advances in Water Science，2009，20(6):885-890. (in Chinese))

［12］刘芳.径向基函数配点法的应用及其误差估计［D］.苏州:苏州大学，2008.

［13］ROCCA A L，POWER H. A double boundary collocation hermitian approach for the solution of steady state convection-diffusion problems ［J］. Computers and Mathematics with Applications，2008，55:1950-1960.

［14］CHEN W，TANAKA M. New insights into boundary-only and domain-type RBF methods［J］. International Journal of Nonlinear Sciences and Numerical Simulation，2000，1(3):145-152.

［15］魏义坤.径向基函数插值法解偏微分方程及计算渗流问题［D］.成都:成都理工大学，2009.