偏磨套管破裂强度三维弹塑性有限元分析

陈占锋 朱卫平 狄勤丰 李世强

（1.上海大学、上海市应用数学和力学研究所，上海 200072；2.上海市力学在能源工程中的应用重点实验室，上海 200072）

随着石油工业中深井、超深井、大斜度井和大位移井的数量增多，套管磨损问题也日显突出。偏磨是套管磨损的一个显著特征，其是钻进过程中钻杆与套管在径向、轴向发生不同程度的碰磨造成［1-3］。套管偏磨会使其承载能力降低，严重时导致套管柱挤毁或破裂，甚至造成全井报废［4-5］。虽然大部分油井套管外壁包裹水泥环，但有时存在水泥环空缺的可能性。在有些井中，为了节省成本，部分技术套管的水泥返高未达地面，使得套管外壁环空依然存在。因此，环空套管偏磨后的承压能力评估和预测，对钻井、完井、采油及修井作业方案设计都有十分重要的意义。

目前国内外对于以外压为主的偏磨套管挤毁强度做过许多理论和实验研究，而对以内压为主的偏磨套管破裂问题研究相对较少，API 标准中也没有专门针对偏磨套管的内压强度或破裂强度计算公式。杨龙［1-2］等人基于弹性理论用有限元法对内壁偏磨套管的内压强度系数进行了分析，将套管内壁的等效应力达到屈服强度时的内压作为临界内压。郑传奎［3］等人在弹性范围内按照平面应变和平面应力理论用有限元法分析了套管本体内壁不均匀磨损对内压强度的影响。Huang［6］采用二维弹塑性有限元法计算了几何缺陷对套管破裂压力的影响。最近，塔里木油田某井发生的套管泄漏复杂情况，已经查明与套管偏磨有关。实际上，偏磨套管在过量内压作用下发生破裂属于弹塑性大变形问题，而且局部为三维过程。为此，本文建立三维弹塑性有限元模型，利用有关实验数据，探寻合适的强度准则，分析偏磨套管破裂机理及其主要影响因素和一般规律，为偏磨套管极限内压强度评估提供理论依据。

1 有限元分析

1.1 几何模型

钻杆在钻进过程中的轴向运动和旋转运动，和套管在径向和轴向发生不同程度的碰磨，按横截面形状可划分为均匀磨损横截面和偏心磨损横截面。本文重点讨论偏心磨损套管，将无磨损不偏心套管作为特例。偏心磨损套管又有两种常见的模型，一种是“月牙形”模型，其主要由钻杆长时间碰磨套管某一侧形成；另一种为“偏心筒”模型，其主要由钻杆不规则碰磨套管内壁形成（图1）。

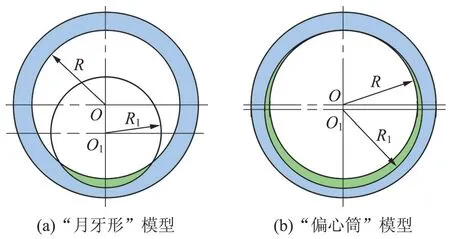
图1 套管偏心偏磨模型

对于“月牙形”模型，当R1＜R 且δ ≠0 时，偏磨率η 可定义为最大偏磨量与套管壁厚的比值，即

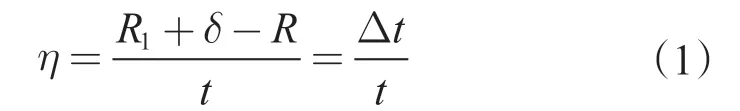
式中，R1为偏磨半径，mm；δ 为套管圆心O 与偏磨圆心O1的距离，mm；R 为套管内圆半径，mm；t 为套管壁厚，mm；Δt 为最大偏磨量，mm。

对于“偏心筒”模型，当R1＞R 且δ ≠0 时，偏心率ξ 可定义为

式中，tmax表示磨损后套管最大壁厚，mm；tmin表示磨损后套管最小壁厚，mm。

将式（2）进一步化简为

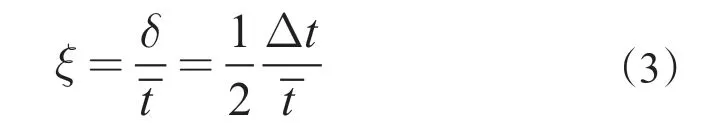
其中 δ= R1- R=(tmax-tmin)/2

最大磨损量相同时，由式（1）和式（3）可得

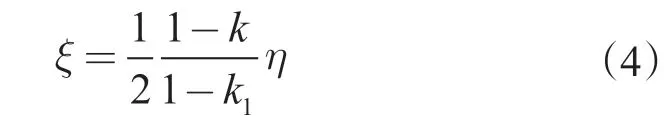
其中 k=R/R0；k1=R1/R0

式中，R0为套管外圆半径，mm。

当R1＞R 且δ=0 时，套管为均匀磨损，磨损后套管壁厚相等。最大偏磨量不变时，随偏磨半径的增大，磨损套管依次可用“月牙形”模型、“偏心筒”模型和均匀磨损模型表示。

1.2 有限元计算

套管在破裂过程中变形较大，是一种局部的三维问题，且材料经历了弹性阶段和塑性阶段，因此建模时需要考虑三维的材料非线性和几何非线性问题。部分技术套管外壁存在环空，本文针对环空套管进行建模与计算。套管并非理想圆管，壁厚也不是完全均匀的，存在一定的几何缺陷，主要表现在内外圆初始椭圆和初始偏心（内外圆不同心）。由于内压能自动校正椭圆度，在此忽略套管内外圆初始椭圆的影响，仅考虑“月牙形”偏磨和“偏心筒”偏磨对套管破裂强度的影响。

采用ABAQUS 进行三维有限元建模和计算，并假设：（1）套管为各向同性弹塑性体，选用C3D20R 单元（20 节点二阶减缩实体单元）进行计算；（2）套管外壁环空（无水泥环固结）仅受均匀内压，忽略外压、轴向力、弯矩、扭矩等其他载荷影响；（3）考虑套管偏磨，且磨损缺陷沿所截取套管的长度方向一致，忽略套管的其他缺陷；（4）忽略残余应力的影响。

算法采用修正的Riks 法，该算法能边计算位移边调节载荷的大小和方向，能在结构不稳定阶段获得静态平衡。模拟过程中内压方向随套管变形而自动改变，时刻保持与套管内壁垂直。内压从0 开始施加并逐渐增大，达到最大值后，有限元程序自动降低套管内压，使得整个套管破裂模拟过程得以继续进行。后处理中可绘出整个模拟过程中套管上任一点的内压—等效应变曲线，如图2 所示，其中a～d 各点所对应的应力、变形状态如图3 所示。不管是偏磨套管还是未偏磨套管，本文将内压—等效应变曲线中最高点（图2 中b 点）对应的压力作为破裂压力。

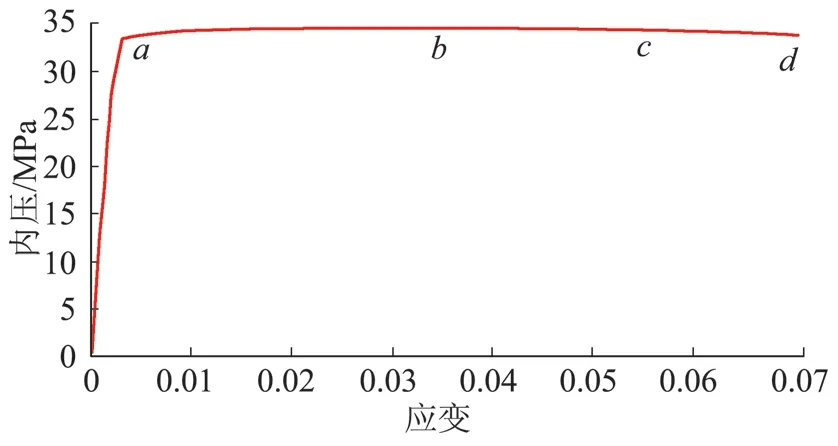
图2 套管破裂过程中的内压与等效应变曲线

图3 套管破裂过程中的等效应力和变形

1.3 材料本构关系

材料本构关系是影响模拟精度的关键因素之一。内压下套管的破裂属于弹塑性变形破坏，变形前后尺寸有较大改变，因此应力—应变关系宜采用塑性力学中的真应力和真应变加以描述，以区别于通常在小变形假设下的（不计尺寸改变影响）工程应力和工程应变。真应力—真应变关系可表示为［7］

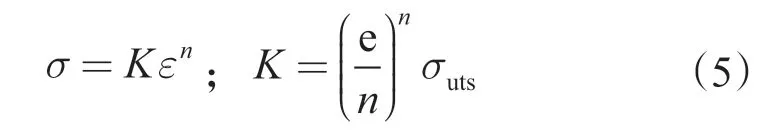
式中，σ 为真实应力，MPa；ε 为真实应变；e 为自然常数；n 为材料强化系数，由单轴拉伸实验确定，n=ln（1+εuts）；εuts为极限应变；σuts为极限强度。

2 偏磨套管破裂机理及强度准则

2.1 破裂机理分析

偏磨套管在内压下破裂属于三维弹塑性大变形破坏问题。套管偏磨后的最薄处存在一定的应力集中，其内壁首先屈服并逐渐向外壁扩展，最后屈服面贯穿整个壁厚，破裂发生。具体情况相当复杂，有些套管要等到内壁达到极限强度才破裂，极少数当外壁接近极限强度时才破裂，即使是无偏磨套管目前还没有一个公式能概括所有情况。其原因除变形复杂外，还在于各种套管的厚径比及材料性质不同。几何偏心、偏磨等缺陷更增加了预测套管破裂压力的难度。破裂强度这里指套管承受内压的极限强度，达到该强度意味着破裂即刻发生。

2.2 强度准则

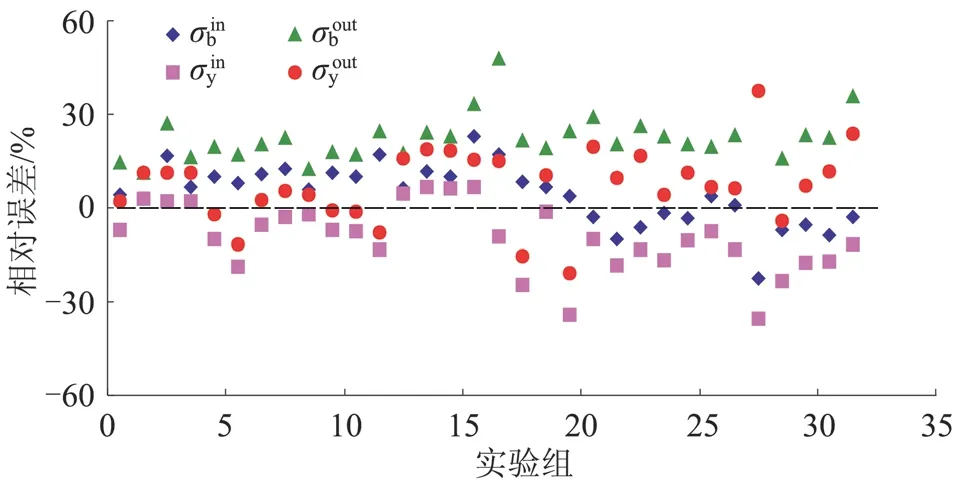
图4 不同强度准则的相对误差

3 偏磨套管破裂压力的影响因素

3.1 偏磨半径对破裂压力的影响

由图1 可见，当偏磨半径R1从小于套管内径R起逐渐增加，偏磨形式自然从“月牙形”模型变化到“偏心筒”模型。以表1 中的TP140 套管为例，首先假定套管最大偏磨量保持不变，为初始壁厚的一半，按本文有限元法计算不同偏磨半径R1所对应的破裂压力，比较不同偏磨形式下破裂压力的变化，结果见图5。可以看出，最大偏磨量相同的情况下，除非偏磨半径很大，套管破裂压力几乎与偏磨半径无关，即套管破裂压力几乎与偏磨形式无关。同时意味着，仅就破裂压力而言，不管是计算还是实验，为了方便，“偏心筒”模型与 “月牙形”模型可以互换。

表1 不同套管的几何尺寸及材料参数

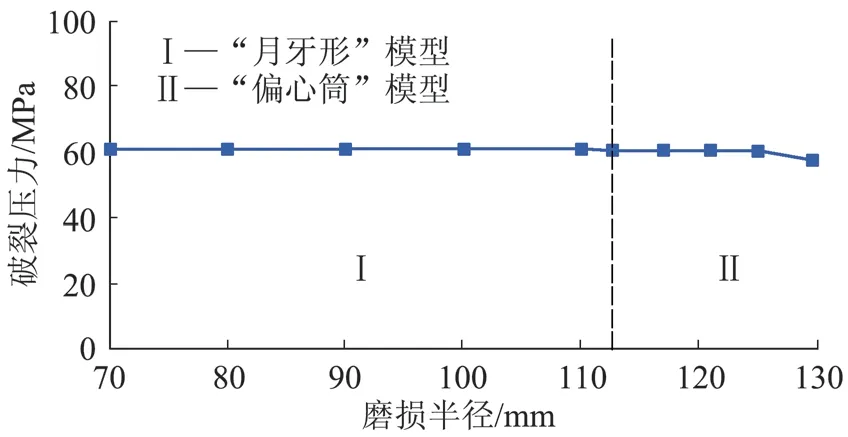
图5 破裂压力与偏磨半径关系

3.2 偏磨率对破裂压力的影响

“月牙形”模型是套管偏磨的主要形式之一。现场实测表明，回收套管中有50%是“月牙形”偏磨［10］。由式（4）可知，最大磨损量一定时，“偏心筒”模型中的偏心率可由“月牙形”模型中的偏磨率表示，因此，此节仅讨论偏磨率对套管破裂压力的影响。以P110套管为例，几何尺寸和材料参数见表1，现假定偏磨半径为60 mm 保持不变，探讨偏磨率与套管破裂压力的关系。本文有限元法计算结果和实验数据对比见表2，实验数据来自文献［5］，磨损率为0 的点对应于无偏磨套管，其他点对应偏磨套管。可以看出，本文有限元法计算结果与实验数据基本吻合，随着偏磨率的增大，破裂压力近似呈线性下降。

表2 偏磨率对套管破裂压力的影响

4 结论

（1）建立了考虑材料非线性和几何非线性三维套管有限元模型，针对内压下套管破裂问题进行研究，提出了新的判断套管是否破裂的强度准则，并依据此准则对偏磨套管的破裂强度进行了初步的探讨。

（2）在套管外径、内径和最大磨损量相等的条件下，偏磨半径对套管破裂强度影响较小，偏磨形式几乎与破裂压力无关， “月牙形”模型和“偏心筒”模型可以相互代替。对于偏磨套管，破裂压力随偏磨率的增加近似呈线性下降。

（3）地层条件复杂多变，载荷也较为复杂，可进一步在本文基础上讨论套管在复合载荷下的破裂强度，以及水泥环和残余应力对套管破裂强度的影响。

［1］ 杨龙，高智海，练章华，等.磨损对套管接头拉伸与内压强度的影响［J］.石油机械，2003，31（10）：9-11，15.

［2］ 杨龙，练章华，高智海，等.套管内壁磨损对其抗内压性能的影响［J］.天然气工业，2003，23（6）：94-96.

［3］ 郑传奎，覃成锦，高德利.含磨损缺陷套管抗内压强度数值计算研究［J］.天然气工业，2006，26（1）：76-79.

［4］ 孙永兴，林元华，廖平，等.ISO10400 油管套管抗内压爆裂设计［J］.石油钻探技术，2010，28（3）：67-69.

［5］ 魏玲，林元华，杜仁德，等. 月牙形磨损缺陷套管的抗内压强度研究［J］.机械科学与技术，2010，29（4）：476-479.

［6］ HUANG Xiaoguang, CHEN Yanyun, LIN Kai, et al. Burst strength analysis of casing with geometrical imperfections ［J］. Journal of pressure vessel technology, 2007, 129（4）∶ 763-770.

［7］ STEWART G, KLEVER F J, RITCHIE D. Analytical model to predict the burst capacity of pipelines［C］. The 13th International Conference of Offshore Mechanics and Arctic Engineering .Vol.Ⅴ, Pipeline Technology, Houston, USA, 1994∶ 177-188.

［8］ AMANO K, MATSUOKA M, ISHIHARA T, et al. Significance of yield ratio limitation to plastic deformation of pipeline in high pressure proof test［C］. Seventh Symposium on Line Pipe Research, Houston, 1986.

［9］ PASLAY P, CERNOCKY E, WINK R. Burst pressure prediction of thin-walled, ductile tubular subjected to axial load［R］. SPE 48327, 1998.

［10］ SONG J S, BOWEN J, KLEMENTICH F. The internal pressure capacity of crescent-shaped wear casing ［R］. SPE 23902, 1992.