宽浅河流水质模型参数灵敏度的空间变化规律

张巧玲，韩龙喜，李洪晶，黄 瑞，3，张 琳

(1.河海大学环境学院，江苏南京 210098;2.河北省水利水电第二勘测设计研究院，河北石家庄 050021;3. 扬州环境资源职业技术学院，江苏扬州 225217)

灵敏度分析用于定性或定量地评价模型参数误差对模型结果产生的影响，是模型参数变化过程和模型校正过程中的有用工具，通过灵敏度分析可以确定对模型有较大影响的参数。目前，灵敏度分析已应用于很多模型的参数敏感性确定及模型的稳定性研究。陈建等［1］采用扰动分析方法定义模型参数的灵敏度，并基于SWAT 分布式水文模型研究了模型参数灵敏度在年内夏季和冬季的变化及其对水文过程模拟结果的影响;林杰等［2］基于Morris 筛选法，采用厦门城市小流域8 场实测降雨数据对城市降雨径流模型SWMM 的水文水力模块进行局部灵敏度及其稳定性分析;束龙仓等［3］将局部灵敏度分析和全局灵敏度分析引入地下水数值模型的参数灵敏度分析中，以塔里木河下游为例，选取含水层渗透系数、给水度、河床沉积物渗透特性系数及河流水位进行地下水数值模拟的参数灵敏度分析，认为地下水数值模型比较稳定，可以用于模拟塔里木河下游地下水水位变化情况;薄会娟等［4］基于新安江模型较多的参数，采用水文模拟法和摩尔斯分类筛选法对清江流域的一次洪水进行径流模拟，应用局部灵敏度分析方法对模型参数进行灵敏度分析，并确定了灵敏参数与不灵敏参数;蒋颖等［5］基于大型流域管理分布式机理模型——WARMF 模型，选定巢湖流域杭埠—丰乐河子流域为研究区域，采用局部灵敏度分析方法对模型水文、泥沙、水质等主要参数进行灵敏度分析。

综合目前的研究成果，可知水质模型解析解的参数灵敏度研究甚少。本研究根据二维水质模型解析解和灵敏度定义，探讨宽浅河流水质模型参数灵敏度空间变化规律，通过建立二维稳态源水质模型、二维瞬时源水质模型，重点分析模型中降解系数、纵向扩散系数、横向扩散系数的灵敏度空间变化规律。

1 研究方法

1.1 研究区域概化

苏子河为大伙房水库上游一级支流，发源于新宾县红升乡关家五凤楼山上，海拔753.5 m，全长119 km，经上夹河古楼村流入大伙房水库，年径流量6 872 亿m3，流域面积2 288.3 km2。苏子河区域内的水文站有占贝水文站，水质监测站分布在古楼大桥断面、红升水库入口断面。

本研究选取2007 年8 月占贝水文站水位-流量实测水文资料进行苏子河水动力模拟。模型模拟所需河道流量参数为河宽90 m，水深1.2 m，流量56.4 m3/s。

1.2 灵敏度定义

灵敏度是反映系统的输出变量对系统特性或参数变化的敏感程度。参数灵敏度反映了函数自变量(参数)的取值误差对函数值的影响程度，水质模型中的参数灵敏度为参数值变化率，可表示为偏导数∂y/∂x。根据灵敏度定义，为了便于计算，可采用有限差分将灵敏度近似表达成:在其他参数不变的情况下，参数x0计算结果值是y0，当初始参数x 变化为±Δx，则有x1=x0-Δx，x2=x0+Δx，相应的结果值应为y1和y2。灵敏度S 的数学表达式为

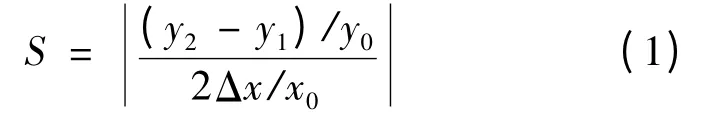
本研究中取Δx=0.1x0。

1.3 参数确定

需要确定的模型参数有纵向扩散系数Ex、横向扩散系数Ey、污染物降解系数K。

a. 纵向扩散系数Ex。Ex为剪切分散与紊动扩散之和，采用如下公式计算:

式中:αx为经验系数，取值4.0;h 为河流平均水深;u*为摩阻流速;g 为重力加速度;J 为水力坡降。

b. 横向扩散系数Ey。采用如下公式计算:

式中:αy为经验参数，取值0.5

c. 污染物降解系数K。可采用监测资料对降解系数进行率定，或根据经验得到。

1.4 参数取值及模拟结果

根据1.3 中参数确定方法确定纵向扩散系数、横向扩散系数和污染物降解系数，具体参数取值和模拟结果为:Ex=0.184 m2/s，Ey=0.023 m2/s，K =1.157×10-6s-1，平均流速u =0.65 m/s，平均水深h =1.2 m。

2 研究结果及其分析

2.1 二维稳态源模型参数灵敏度空间分布规律

采用空间二维方法模拟预测排污口下游污染物浓度平面的分布时，影响预测结果的主要水质参数有降解系数、纵向扩散系数、横向扩散系数。研究表明，纵向扩散系数影响甚微，可只考虑横向扩散系数的影响，相应的二维稳态源模型解析解为

式中:ρ(x，y)为(x，y)处的污染物质量浓度，mg/L;m 为排放点源单位时间的排污量，g/s;x 为纵向距离，m;y 为横向距离，m。

2.1.1 污染物中心排放

根据二维稳态源解析解数学模型、灵敏度计算公式，降解系数、横向扩散系数的灵敏度的表达式为

由苏子河水文参数值及模拟结果，依据二维稳态源模型参数灵敏度表达式得到排污口下游不同预测断面处降解系数、横向扩散系数的灵敏度表达式。图1、图2 分别为稳态源中心排放时降解系数、横向扩散系数的灵敏度空间分布图。

图1 稳态源中心排放时降解系数的灵敏度空间分布

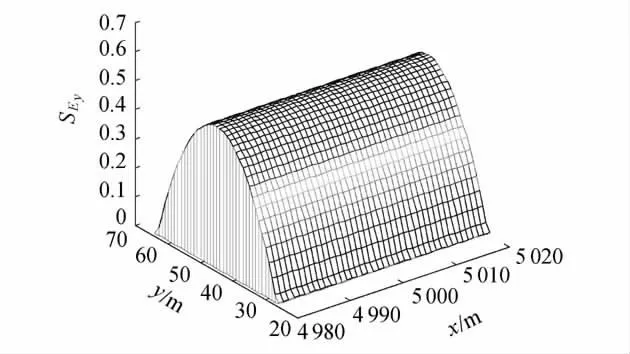
图2 稳态源中心排放时横向扩散系数的灵敏度空间分布

计算结果显示，在给定河流参数情况下，降解系数灵敏度仅与沿程纵向距离有关。中心排放时，污染物自排污口向下游迁移过程中，随着流程的不断增加，污染物累积降解数量也随之增大，降解系数对污染物自净效应的影响也不断增大，由图1 可知，降解系数的灵敏度随着预测距离的增加而增加，与预测距离成正比例关系。

同样地，污染物自排污口向下游迁移过程中，当排放至下游22 891 m 时，污染物达到全断面充分混合，因此中心排放时，二维模型适用于排放口至下游22 891 m 的距离。计算结果显示:该距离内不同空间位置处灵敏度分布呈现相似规律。选取距排污口4980 ～5020 m 的河段，排污口所在中心线两侧各20 m 的距离来分析稳态源中心排放横向扩散系数灵敏度空间分布特征。由图2 可知，稳态源污染物中心排放时，随着污染物自河中心向河两岸扩散，污染物横向扩散效应逐渐增大，横向扩散系数的灵敏度横向范围逐渐向河两岸扩大，其空间分布规律为:以排污口所在中心线为对称轴，灵敏度向河岸两边逐渐减小，灵敏度变化范围为0.04 ～0.51。

2.1.2 污染物岸边排放

污染物岸边排放时，降解系数的灵敏度与排污口的横向位置无关，因此，只需考虑横向扩散系数的灵敏度空间分布规律。

根据均匀流中稳态源二维解析解数学模型、灵敏度计算公式，横向扩散系数灵敏度的表达式为

由苏子河水文水质参数值及模拟结果，依据二维稳态源模型参数灵敏度表达式，得到排污口下游不同预测断面处横向扩散系数的灵敏度。图3 为稳态源岸边排放时横向扩散系数灵敏度空间分布图。

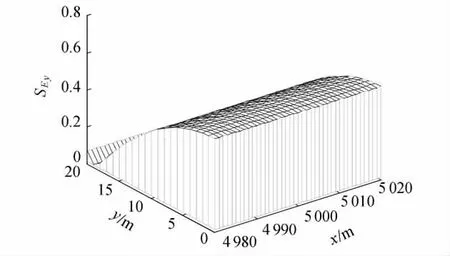
图3 稳态源岸边排放时横向扩散系数的灵敏度空间分布

稳态源污染物岸边排放时，污染物自排污口向下游迁移过程中，当排放至下游91 565 m 时，污染物达到全断面充分混合，因此岸边排放时，二维模型适用于排放口至下游91 565 m 的距离。该距离内不同空间位置处的灵敏度分布呈现相似规律。选取距排污口4 980 ～5 020 m 河段，距排污口所在河岸20 m范围来分析稳态源岸边排放时横向扩散系数灵敏度的空间分布特征。由图3 可知:稳态源污染物岸边排放时，随着污染物向河中心扩散，污染物横向扩散效应逐渐增大，横向扩散系数灵敏度横向范围逐渐向河中心扩大，其空间分布规律为排污口所在断面灵敏度最大，并随横向距离逐渐减小，变化范围为0.04 ～0.51。

2.2 二维瞬时源模型参数灵敏度空间分布规律

均匀流二维瞬时源模型解析解为

式中:ρ(x，y，t)为t 时刻(x，y)处的污染物质量浓度，mg/L;M 为瞬时源强度，g/m;t 为污染物排放时间，s。

2.2.1 污染物中心排放

根据均匀流中瞬时源二维解析解数学模型、灵敏度计算公式，降解系数、纵向扩散系数、横向扩散系数的灵敏度的表达式为

式中:SEx为纵向扩散系数灵敏度;ΔEx为纵向扩散系数变化量，m2/s。

由苏子河水文水质参数值及模拟结果，依据二维瞬时源参数灵敏度表达式，得到排污口下游不同预测断面处降解系数、纵向扩散系数、横向扩散系数的灵敏度。图4(a)、(b)、(c)分别为瞬时源中心排放时降解系数、纵向扩散系数、横向扩散系数的灵敏度空间分布图。

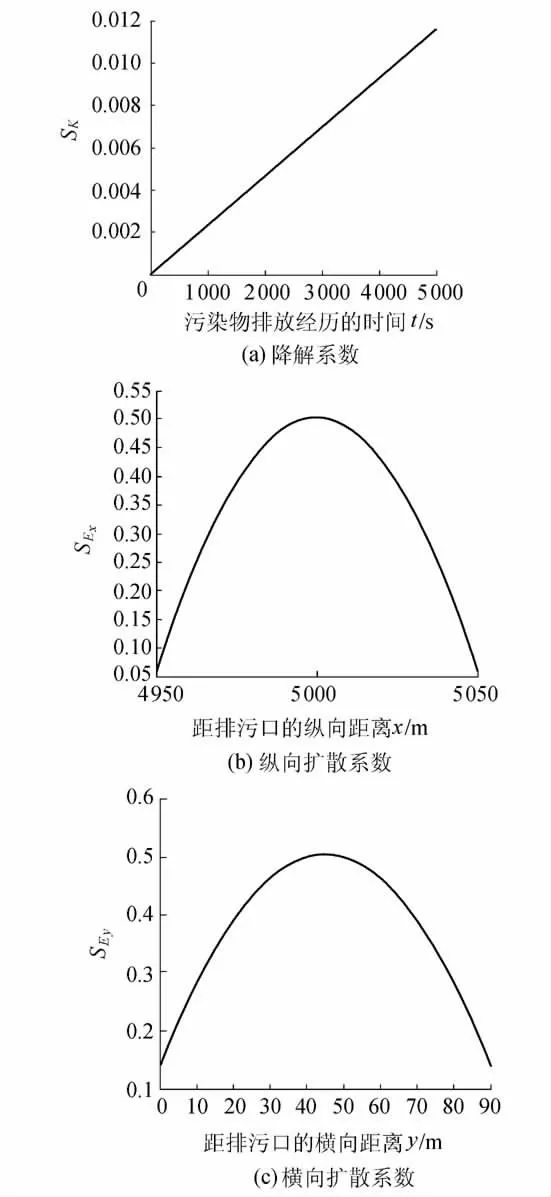
图4 瞬时源中心排放时降解系数、纵向扩散系数和横向扩散系数的灵敏度空间分布

由图4(a)可知:瞬时源污染物中心排放时，污染物自排污口向下游迁移的过程中，随着流程的不断增加，降解系数的灵敏度与污染物排放时间成正比，即与扩散距离成正比。

污染团自排污口向下游迁移过程中，不同空间位置处的灵敏度分布呈现相似规律。选取距排污口4 950 ～5 050 m 河段，排污口所在中心线两侧各35 m范围来分析瞬时源中心排放时扩散系数灵敏度的空间分布特征。由图4(b)可知:瞬时源污染物中心排放时，随着污染团向下游迁移，污染团纵向扩散效应逐渐增大，其灵敏度纵向空间范围向上下游逐渐扩大，不同时刻灵敏度呈现相似的类抛物线分布，即以污染团横向中心线为对称轴且向上下游逐渐减小，变化范围为0.05 ～0.51。由图4(c)可知:随着污染团向下游迁移，污染团横向扩散效应逐渐增大，其灵敏度横向空间范围逐渐向河两岸扩大，不同时刻灵敏度呈现相似的类抛物线分布，即以污染团横向中心线为对称轴，灵敏度向河两岸逐渐减小，变化范围为0.14 ～0.51。

2.2.2 污染物岸边排放

由于降解系数、纵向扩散系数的灵敏度与排污口的横向位置无关，因此，污染物岸边排放时，只需考虑横向扩散系数的灵敏度空间分布规律。

根据均匀流中瞬时源二维解析解数学模型、灵敏度计算公式，横向扩散系数灵敏度的表达式为

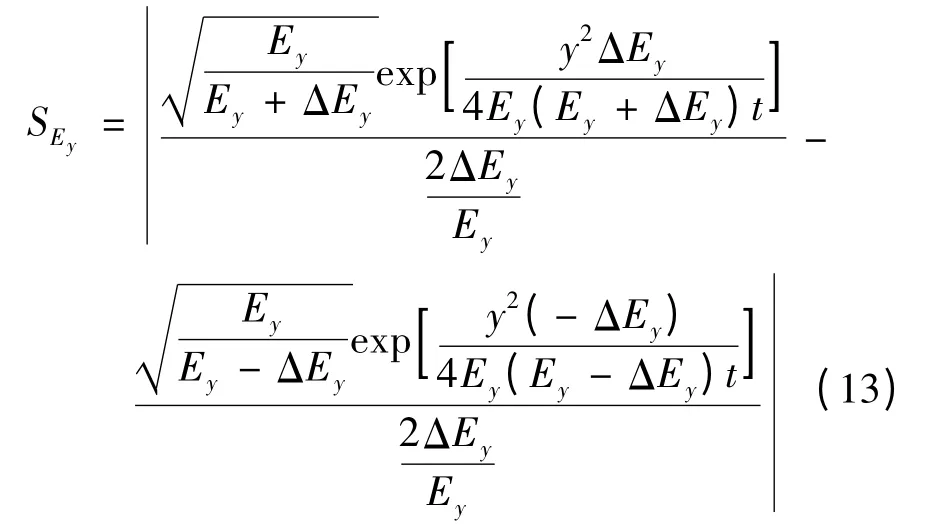
由苏子河水文水质参数值及模拟结果，依据二维瞬时源参数灵敏度表达式可计算出排污口下游不同预测断面处横向扩散系数的灵敏度。图5 为瞬时源岸边排放时横向扩散系数的灵敏度空间分布。

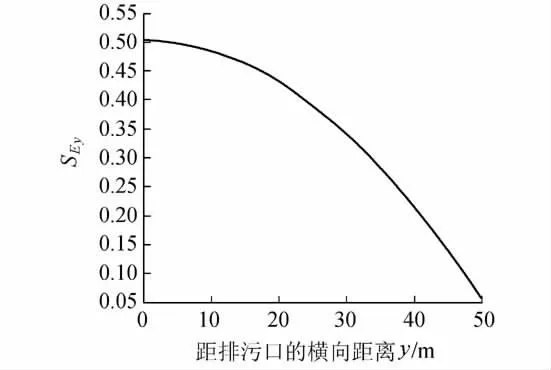
图5 瞬时源岸边排放时横向扩散系数的灵敏度空间分布

计算结果显示:瞬时源污染物岸边排放时，污染团自排污口向下游迁移过程中，不同空间位置处灵敏度分布呈现相似规律。选取纵向距离距排污口5 000 m 河段，横向距离距排污口所在河岸50m 范围来分析瞬时源、岸边排放时横向扩散系数灵敏度的空间分布特征。由图5 可知:瞬时源污染团岸边排放时，随着污染团向下游迁移，污染团横向扩散效应逐渐增大，其灵敏度横向范围逐渐向河中心扩展，不同时刻灵敏度呈现相似的空间分布，其分布特征为:污染团中心所在断面灵敏度最大，并随横向距离逐渐减小，变化范围为0 ～0.51。

3 结 论

a. 宽浅河流水质模型解析解中，降解系数灵敏度与预测距离成正比;横向扩散系数的灵敏度空间分布特征与源的形式、污染物排放位置等有关。

b. 二维水质模型解析解中，在给定设计流量、给定源的形式下，横向扩散系数灵敏度最大值是一致的。

c. 二维稳态源、二维瞬时源水质模型解析解中，在给定设计流量的条件下，模型的横向扩散系数较降解系数灵敏，这为模型率定时模型选择参数初始值提供了依据。

［1］陈建，梁川，陈梁. SWAT 模型的参数灵敏度分析:以贡嘎山海螺沟不同植被类型流域为例［J］.南水北调与水利科技，2011，9(2):41-45. (CHEN Jian，LIANG Chuan，CHEN Liang. Parameter sensitivity analysis of SWAT Model:a case study of small watersheds with different land cover types in Hailuogou valley［J］. South-to-North Water Diversion and Water Science ＆ Technology，2011，9(2):41-45.(in Chinese))

［2］林杰，黄金良，杜鹏飞，等.城市降雨径流水文模拟的参数局部灵敏度及其稳定性分析［J］. 环境科学，2010，31(9):2023-2028. (LIN Jie，HUANG Jinliang，DU Pengfei，et al.Local sensitivity and its stationarity analysis for urban rainfall runoff modelling［J］.Environmental Science，2010，31(9):2023-2028.(in Chinese))

［3］束龙仓，王茂枚，刘瑞国，等.地下水数值模拟中的参数灵敏度分析［J］. 河海大学学报:自然科学版，2007，35(5):491-495. (SHU Longcang，WANG Maomei，LIU Ruiguo，et al.Sensitivity analysis of parameters in numerical simulation of groundwater［J］.Journal of Hohai University:Natural Sciences，2007，35(5):491-495.(in Chinese))

［4］薄会娟，董晓华，邓霞.新安江模型参数的局部灵敏度分析［J］. 人民长江，2010，41(1):25-28. (BO Huijuan，DONG Xiaohua，DENG Xia. Local sensitivity analysis on parameters of Xinanjiang Model［J］. Yangtze River，2010，41(1):25-28.(in Chinese))

［5］蒋颖，王学军，罗定贵. 流域管理模型的参数灵敏度分析:以WARMF 在巢湖地区的应用为例［J］.水土保持研究，2006，13(3):165-168.(JIANG Ying，WANG Xuejun，LUO Dinggui. Parameters sensitivity analysis of watershed management model:application of WARMF model in Chaohu Lake area［J］. Research of Soil and Water Conservation，2006，13(3):165-168.(in Chinese))