煤巷锚杆支护技术的探讨
曹子文
(山西煤炭运销集团 泰安煤业有限公司,山西 保德 036604)
1 锚杆支护技术的概述
锚杆支护是煤巷支护技术的发展方向。实践表明,它与传统棚式支护相比,锚杆支护可以改善支护效果、降低成本、加快速度、减轻劳动强度、提高断面利用率等优越性,是煤矿高产高效生产的重要配套技术。锚杆支护的目的,是使巷道围岩达到稳定。本文从巷道围岩的变形特征出发,分析锚杆支护的作用及效果。
2 典型巷道围岩的变形特征
调查与实测表明,大部分巷道的破坏是渐进形成的,围岩松动范围也是随着时间逐渐扩展的;巷道周边一定范围的围岩内,巷道各点的变形速度及变形量差异较大:深部的围岩变形小、速度慢,而浅部围岩变形大、速度快。即使是完全处于塑性区的巷道,围岩内部变形差异也是存在的,并在不同的围岩深度还存在拉压域。深部围岩受压,而浅部受拉。不同位置围岩之间变形量与变形速度的差异,会导致围岩的进一步变形或相互约束。若能在实际中,仔细分析其相互作用、明确其相互作用的范围和条件、充分考虑实现围岩的自我约束条件,利用围岩的这一变形不协调性来实现围岩相互约束,则可减少巷道变形。锚杆的作用首先是实现或增强围岩的自身稳定,其次才考虑其进一步的加固作用,控制围岩的变形量,从而达到安全目的。
3 锚杆支护的作用分析
1)悬吊作用论。锚杆的支护作用最早为悬吊理论,巷道表层的围岩用锚杆悬吊起来,锚固在深层的围岩上,这种解释存在一定的局限性。例如巷道围岩存在形状和大小合适的破碎围岩体,且此围岩体在不支护的条件下可能自行垮落,这时若用锚杆将其悬吊起来、以保持巷道周边的完整性,则锚杆的悬吊理论是成立的;否则是不成立的。
2)组合梁理论。众所周知,煤系地层的围岩大多是层状的,即使是同一种岩性,也表现为层状,典型的为泥岩、页岩,有时层理还较发育,若用锚杆把这些层状的围岩锚固成一个整体,则可增强承载能力。这种组合梁理论也存在其缺陷。例如围岩相对破碎,但靠自身的摩擦和相互挤压能够达到自身稳定时,采用组合梁理论解释,其理由就不够充分。
3)组合拱理论。组合拱理论恰好解释了组合梁理论不能解释的问题。例如相对破碎但在一定条件下可以自稳的围岩,采用组合拱理论解释是很完美的,尤其是巷道断面大或一些拱形巷道,用组合拱理论解释非常贴近实际。锚杆把这些相对破碎的围岩进行组合,防止其进一步移动垮落,再靠围岩自身的摩擦、相互挤压形成承载能力较强的拱形结构,阻止围岩的进一步变形,从而达到安全目的。
以上是传统的三种假说,从不同角度、条件解释了锚杆支护的作用机理,力学模型简单、计算方法简便。近年来,又提出了巷道锚杆支护围岩强度强化理论及最大水平应力理论,主要是针对锚杆的受力状况提出来的,揭示了锚杆支护的实质,扩大了锚杆支护技术的应用范围,为巷道锚杆支护设计提供了理论指导。
4 锚杆支护设计的理论分析
锚杆支护设计考虑的因素较多,主要有:巷道围岩的赋存特征及其物理力学特性;巷道围岩的受力状况及主应力方向与巷道轴线方向的关系;巷道的断面形状尺寸及服务年限。
考虑以上因素设计的锚杆支护参数有:锚杆的长度、直径、锚固长度、锚杆的间距、排距、方向。其传统的设计方法主要如下:
1)经验设计法:
①锚杆长度:L=N(1.5+W/10).
式中:L 为锚杆的总长度,m;N 为围岩影响系数,该矿为Ⅲ类围岩取1.0;W 为巷道或硐室的跨度,m。
②锚杆间距:M≤1.0/N.式中:M 为锚杆间距,m。
③锚杆直径:d=L/110.式中:d 为锚杆的直径,m。
2)规程类比法:表1为常见巷道锚杆参数的取值。
3)极限平衡区设计法:分述如下。
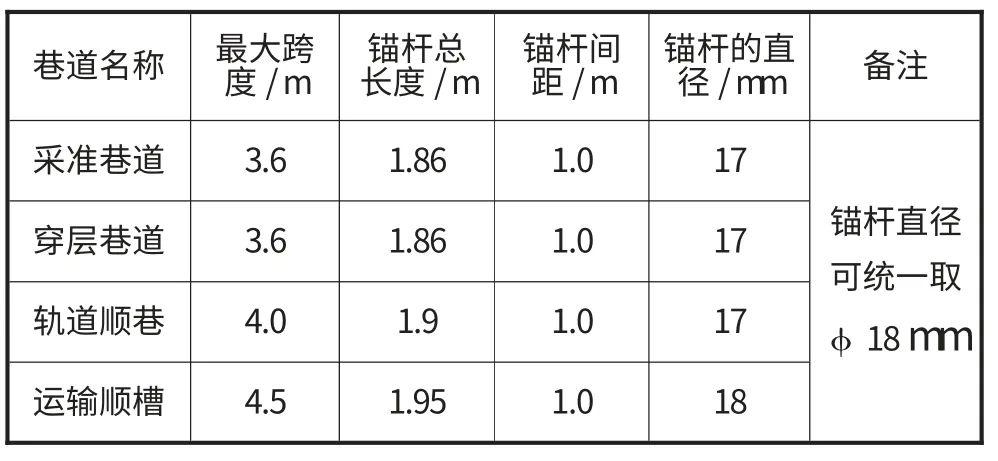
表1 各类巷道锚杆支护参数的经验公计算值
巷道理论半径的确定。巷道理论半径为当量半径与外接圆半径的最小者,当量半径用下式计算:
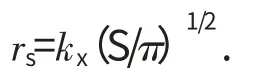
式中:rs为巷道当量半径,m;S 为实际巷道断面积,m2;kx为巷道端面修正系数。
极限平衡半径、巷道周边位移、极限平衡区深入巷道围岩的深度。
根据弹性理论、双向等压情况下,受采动影响圆形巷道的极限平衡区半径R 可表示为:

式中:α 为巷道理论半径,m;γH 为自重应力,kg/cm2;γ为上覆岩层体积质量,kg/cm3;H 为巷道埋深,m;Pi为支护阻力kN;R 为 极限平衡区 半径,m;C 为 黏 结 力kg/cm2;φ 为内摩擦角,°;K1为采动影响系数;K2为岩体力学参数修正系数。
巷道周边位移u 可表示为:

式中:u 为巷道周边位移,m;G 为剪切弹性模量,MPa。λ=(1-sinφ)/2sinφ.极限平衡区深入围岩的深度Δ 为:Δ=R-a.式中:Δ 为极限平衡区深入围岩的深度,m。
3)锚杆长度:L=L1+Δ+L2.式中:L 为锚杆长度,m;L1为锚固长度,m;L2为锚杆外露长度(取0.1m)。按端锚方式安设锚杆,锚固长度L1按黏结段的黏度同锚杆承担的最大载荷相匹配的原则确定。
锚固段内金属锚杆同黏结剂之间总黏结力与锚杆载荷之间满足下式:
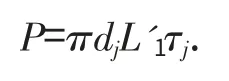
式中:dj为锚杆直径,mm;τj为黏结剂同金属锚杆间的黏结强度,取8MPa;P 为锚杆载荷,MPa;L'1为按破坏面发生在金属锚杆表面处要求的锚固段长度,mm。从而可有L'1=P/(πdjτj)。同理,锚固段内黏结剂同钻孔岩壁之间的的黏结力与锚杆载荷之间应满足下式:
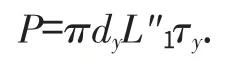
式中:dy为钻孔的直径,mm;τy为黏结剂同钻孔岩壁之.间的的黏结强度;L"1为按破坏面发生在钻孔岩壁处要求的锚固段长度,mm。从而可有L"1=P/(πdjτj).
4)锚杆直径D 与间排距的确定:在载荷集度一定的情况下,锚杆直径同锚杆间排距成反比关系;在每根锚杆负责的维护面积确定的情况下,需支护加固的最大载荷密度为qd=n(R-h)γ.
式中:n 为载荷备用系数,取2;h 为矩形巷道的半高,m。根据每根锚杆所维护的面积S(S=H×I=间距×排距)及载荷集度,可以算出每根锚杆所承担的载荷,从而确定锚杆直径,公式为
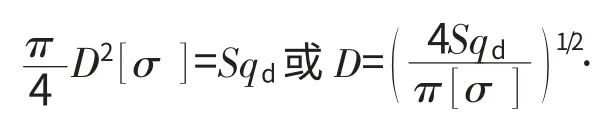
式中:D 为锚杆的直径,mm;[σ]为杆体材料的许用强度,MPa。锚杆直径与锚杆的间排距存在如下关系:

5 结束语
上述设计,基本上考虑了巷道在围岩中的赋存特性,进而从理论方面设计锚杆的支护参数,但是没有考虑主应力方向与巷道轴线的关系,这是目前设计中存在的一个缺陷。再者,巷道围岩的变形并不是连续的、均匀的,可能存在离层,一些岩层的变形量大、另一些小,层与层之间发生离层,这些变形与离层所产生的力都由锚杆来承担,若是端锚、锚杆相对均匀承载,若是全长锚固、则锚杆的受力不均匀,在变形量大的岩层部位、锚杆受力也较大。一般情况下,锚杆的初锚力要达到其额度承载力80%以上,如果围岩变形量超出锚杆的伸长量,锚杆可能拉断或失去承载力。所以本人认为,如果围岩变形不均匀连续,宜用端锚,使锚杆均匀伸长,避免全锚产生局部伸长而拉断锚杆。大部分巷道后期变形量非常严重(也即流变),如超出一定的范围,锚杆可能失去其支护效果而导致巷道垮落。为了适应围岩的大变形,可伸缩锚杆的研制成为当务之急;只有锚杆适应围岩的变形,才能对围岩起到控制作用(也即耦合作用);所以可伸缩锚杆是今后锚杆发展的主要方向之一。

