基于公理设计的多目标优化方法研究

张海杨 田启华，2 杜义贤，2

（1.三峡大学机械与材料学院，湖北宜昌 443002；2.三峡大学水电机械设备设计与维护湖北省重点实验室，湖北宜昌 443002）

公理设计理论是通过对大量成功的设计案例进行分析归纳，并从中抽象出设计过程的本质.公理设计的最终目标如下：为设计活动建立一个科学的模式，为设计人员提供一个基于逻辑和理性思维过程的理论基础，进而来改进设计活动［1］.但公理设计常用于概念设计，很少应用到详细设计阶段中.对于某个给定的结构，多目标优化则是比较有效的设计方法，多目标优化是一个比较具体的过程，更多地涉及到详细设计方面.

多目标优化问题中各目标间往往存在着矛盾，即要求各目标同时达到最优是很困难的，所以最优解不一定存在.而公理设计在处理大规模系统设计问题时有着较强的优势［1］，Liu［2］、Hwang［3］、Jeff［4］和王晓勇［5］等应用公理设计中的独立公理，对多目标优化问题进行了改进.

本文基于公理设计理论中的独立公理，在求解多目标优化设计问题的过程中，运用全参直度S（Semangularity）和全能直度R（Reangularity）分析技术来解决多目标优化问题中设计优劣难以评价的问题.

1 基于公理设计的多目标优化方法

公理设计中的独立公理指出：对于一个能够接受的设计，功能要求（FRs）与设计参数（DPs）之间的映射存在一种特定的关系，即每个功能要求能独立地被满足并且不会影响其他功能要求的实现.它们之间的映射可用以下设计方程式来表示［6］：

可简化为：

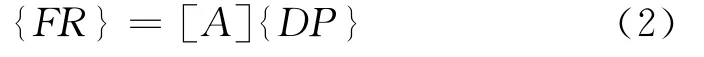
式中，｛FR｝为功能要求集，｛DP｝为设计参数集，［A］为设计矩阵.

若要满足独立公理，设计矩阵就必须是对角矩阵或者三角矩阵.若［A］为对角矩阵，则每一个｛DP｝满足一个｛FR｝，此种设计为无耦合设计.若［A］为三角矩阵，则只有按一定的顺序确定设计参数，才能使功能要求保持独立性，此种设计为解耦设计.除此之外的设计都是耦合设计，耦合设计是违反独立公理的.

公理设计通过两个量化指标R 和S 来度量FRs之间的独立性.R 被用来测量DPs 之间的交互作用，也就是DPs轴之间的角度关系.R 的表达式可表示如下［1］：

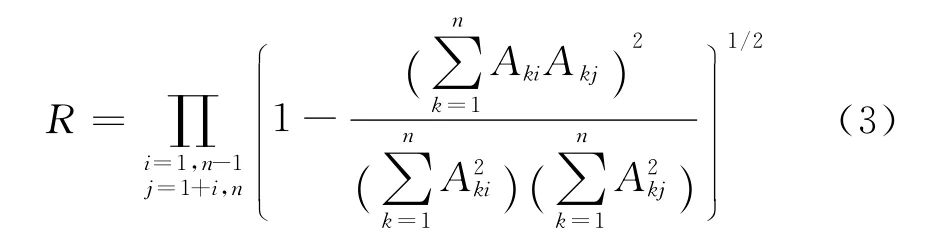
S 被用来测量FRs 和DPs 之间的交互作用，也就是设计矩阵归一化之后其对角线元素的幅值.S 的表达式可表示如下［1］：

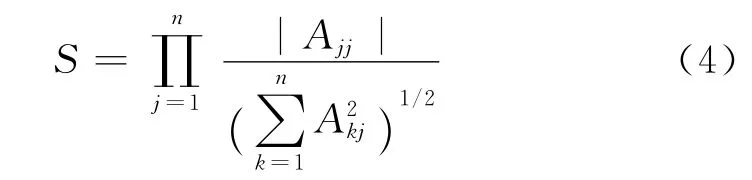
大多数工程设计问题都是多目标的优化设计问题，优化设计的表达式为

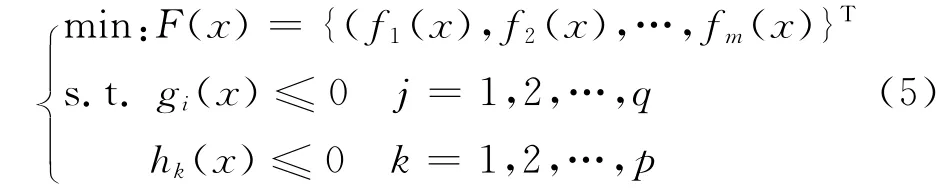
与单目标优化相比，多目标优化在理论与计算方法上都还很不完善，也不够系统［7］.所以，本文引入公理设计来完善多目标优化理论和方法体系.其具体步骤如下：

1）获得设计矩阵.实际上，在优化设计问题中的目标函数就相当于功能需求，也就是公理设计中的｛FR｝，影响目标函数值的参数相当于设计参数｛DP｝（在优化设计中称作设计变量），但在优化设计中，｛FR｝要通过｛DP｝以数学公式的形式来表示.

式（2）可写成如下微分形式：

则设计矩阵可变形为：

2）对设计矩阵进行R／S 分析.目标是找到最优的设计参数，使其尽可能完美地满足各功能需求.

由R、S 的定义可知（如图1所示）：当R＝S＝1时，设计是无耦合设计；当R＝S 但不等于1时，设计被近似地看作是解耦设计；在仅有两个FRs和DPs时，若R＝S，则该设计是解耦设计；其它情况下的设计均为耦合设计.因此，通过R／S 分析可以得到：当设计变量取某一组值时，各目标函数耦合的程度.

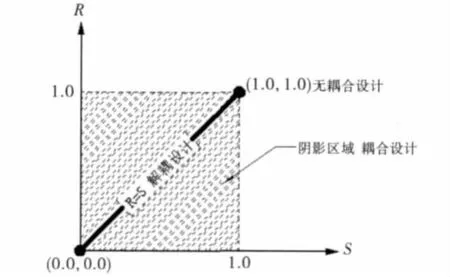
图1 独立空间

3）建立关于R 与S 的目标函数.为了使多目标优化问题简化为可以在二维区域内图形化的问题，并使计算变得相对容易，根据图1将其形式确定如下：

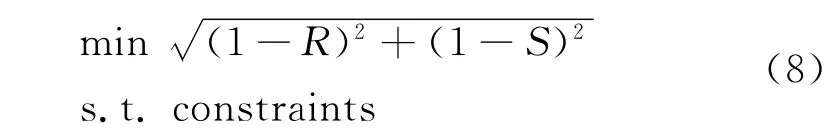
4）利用Matlab强大的数值运算功能和绘图功能，绘制出各目标函数的图形，结合上面步骤得出的结果进行分析.

2 应用分析

2.1 问题求解

以下是一个简单的多目标优化问题，以此来举例说明本文提出的方法.

1）获得设计矩阵.

由式（7）可得设计矩阵

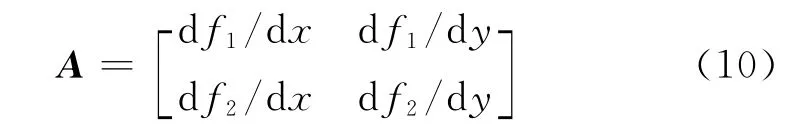
2）对设计矩阵进行R／S 分析.

根据定义域的大小，将设计域均分为4个区域，针对各区域的关键点进行R／S 分析计算.分析结果见表1.

表1 R／S分析结果

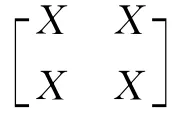
3）建立关于R 与S 的目标函数.

由式（8）可得

4）利用Matlab软件绘制出各目标函数的图形，结合前几步得到的结果进行分析.

由以上分析可得，在功能上无耦合的区域中，目标函数的最小值在x＝5，y＝5处取得.

2.2 应用分析

使用Matlab软件可绘制出以上两个目标函数在边界条件内的三维图形，如图2所示，可以清晰地看出目标函数值的变化趋势.

图2 二目标函数的三维曲面表示

其Matlab代码如下：

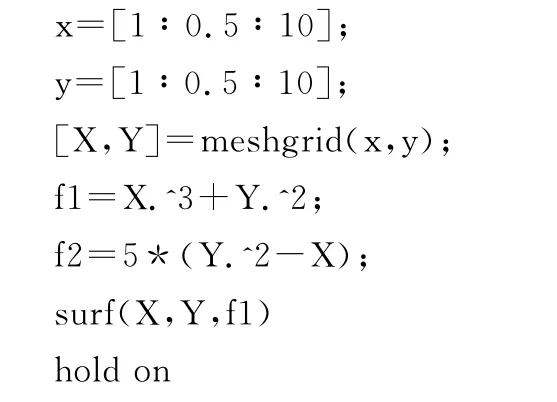
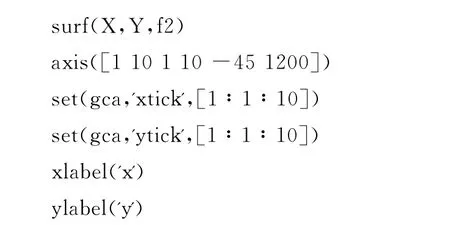
进而使用Matlab软件绘制出以上两个目标函数的二维等高线图，如图3所示.

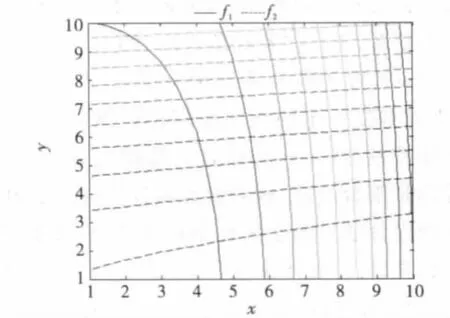
图3 二目标优化问题的二维等高线图

其Matlab代码如下：

下面对图3进行分析.

对于右上区域（点（5，5）和点（10，10）之间的区域），f1与f2近似相互垂直且与y、x 坐标轴各自分别近似平行，系统是近似解耦的.

对于右下区域，只有f1与y 是近似平行的，系统是近似可解耦的.

对于左上、左下区域f1，f2与与y、x 轴都不平行，系统功能上是耦合的.

x，y 与f1，f2之间的关系也可以通过设计矩阵来描述.通过R／S 分析来判断设计矩阵与理想的无耦合矩阵之间的差距.

根据这些分析结果，目标函数的最小值（功能上无耦合）在点（5，5）处取得.因此，该多目标优化问题最优解可以从无耦合的区域中确定.

3 结 语

本文用公理设计理论方法评估多目标优化问题，运用R／S 分析，降低了系统的功能耦合度，达到了更好的设计效果.在今后的研究中可以扩展R 与S 现有的定义，使其包含当设计参数的数目多于目标函数的数目的多目标优化问题.

［1］ S N P.Axiomatic Design：Advances and Applications［M］.New York：Oxford University Press，2001.

［2］ Liu X P，Soderborg N.Improving an Existing Design Based on Axiomatic Design Principles［M］.Boston.Massachusetts Institution of Technology，2000.

［3］ Hwang K H，Lee K W，Park G J，et al.Robust Design of the Vibratory Gyroscope with Unbalanced Inner Torsion Gimbal Using Axiomatic Design［M］.Boston：Massachusetts Institution of Technology，2002.

［4］ Jeff Thielman，Ge Ping.Applying Axiomatic Design Theory to the Evaluation and Optimization of Large Scale Engineering Systems［J］.Journal of Engineering Design，2006，17（1）：1－16.

［5］ 王晓勇，唐敦兵，楼佩煌.基于设计公理的多属性决策方法［J］.西南交通大学学报，2008，43（3）：392－397.

［6］ S N P.公理设计发展与应用［M］.谢友柏，袁小阳，等译.北京：机械工业出版社，2004.

［7］ 黄洪钟，姚新胜，周仲荣.基于满意度原理的装载机工作装置的多目标优化设计［J］.机械工程学报，2003，39（5）：97－103.