象棋机器人视觉识别算法研究
朱一峰
(朝阳师范高等专科学校 教务处,辽宁 朝阳 122000)
0 引言
机器人技术是人工智能、模式识别、机械、仿生学等多学科的交叉学科产物。娱乐机器人的研究已成为机器人研究的重要方向。象棋机器人是娱乐机器人的研究方向之一,视觉系统是象棋机器人研究的关键部分。笔者基于计算机视觉和模式识别技术,研究了象棋机器人视觉算法,针对对弈的实际状况,采用彩色空间变换、阈值分割、形态学骨架化及Hough 变换等图像处理技术对棋局中的棋子进行检测、定位和分割。通过提取棋子旋转不变的径向像素点数作为特征,克服了棋子方向随意性带来的识别问题。
象棋机器人对弈时的实时性要求非常高,而采用各种预处理及Hough 变换抗噪性强时必然要牺牲运算时间。对于开局初始化时,有足够多的时间进行初始化;但是对于对弈进行中时,运算时间就变得很重要。因此在对弈时,采取前后两帧图像相减的方法进行了冗余信息剔除,从而大大节省了运算时间,而且能够保证处理结果的准确性。所以,在本研究中将整个算法流程划分为开局初始化和对弈进行中两个步骤。
1 棋盘及棋子图像的二值化
利用人为的从棋盘字符图中切割出图像的单个灰度字符作为实验对象,对几种二值化方法进行对比,找到规律与影响效果的因素,如图1所示。

图1 单个棋子的二值化结果
通过比较,可以看出几种方法各有各的适宜条件,主要依赖于图像质量。
1)对于由数码相机拍摄、光照均匀、图像质量好的图片,固定阈值法与大津法都可以取得良好的二值效果,它们之间的不同在于大津法二值化的线条要比固定阈值法粗。而此时局部阈值法(3×3 窗口)易出现伪影现象,局部阈值法(5×5窗口)基本可以进行正确的分割,但是它的二值字符线条较细,容易产生不连续。
2)大津法[1]与动态大津法[2]的区别:动态大津法在处理字符线条的直线性方面优于大津法,如图1 中(e)、(f)图中第3 条横线处。但是由于动态大津法是基于分块的方法,在某一块内需要包含有目标与背景像素,而且目标与背景各自内部的灰度变化范围不大。如果在某一块中,只有背景或者含有极少的目标的情况下,这时动态大津法就会出现分割错误,将整个背景区域都作为目标提取出来。
在实际中根据棋子的位置来选择二值化方法。当棋子位置位于图像左右两端时采用大津法二值化,其余位置用固定阈值法。
2 改进Hough 变换求取棋子圆心
Hough 变换[3]是检测圆的有效方法。改进的原因是Hough 变换检测圆所需的时间比较长。本研究采取了径向和纵向取点的方法取得了3 个点。具体算法为:
1)获取图像中任意一亮点A。
2)沿A 点的径向方向相距一定距离的位置开始搜索下一亮点,直至找到满足条件点B。
3)同理,沿纵向方向求取另一点C。
4)根据A、B、C 3 点的坐标求取出图像中圆的圆心及其半径。
5)重复1),2),3),4)步,直到对图像搜索完毕。
当图像比较清晰、特征比较明显时,可以求取出这样的点。实验结果如图2 和图3 所示。

图2 预处理后图像

图3 使用改进的Hough 变换求取的圆心
但是在实际的图像处理过程中,准确找到3 个点不是一件容易的事情。考虑到噪声的影响,可以找出更多的点,提高鲁棒性[4],从而保证处理结果正确。对图4 进行Hough 变换所获取的结果和改进后的Hough 变换获取的结果如表1 所示。

图4 棋子图像

表1 传统Hough 变换和改进后的Hough 变换结果比较
从表1 可见采用改进后的Hough 变换方法,圆心坐标与传统Hough 几乎一致,但是计算时间远远小于传统Hough 变换。
由于棋盘初始化过程有较为充裕的时间,故而笔者对采集的图像采用传统Hough 变换进行初始化处理。这样能够提高所获取初始数据的准确性。而在对弈进行的时候,采用改进的Hough 变换,既能保证准确性,又能提高识别速度,以满足时间上的需要。
3 提取棋子像素特征
像素点是结合提取出的圆心以及细化前后的二值图像进行处理的,处理后能够以圆心所处位置进行附近圆域内像素点统计,本研究取统计半径为棋子内边界半径的0. 95 倍。所使用的图像如图5 所示。

图5 原始图像
没有进行细化的像素点个数统计结果如表2。
对图像进行预处理[5],并且求取细化后的像素点个数见表3。其中包含棋子的坐标及图像的S(饱和度)图像像素统计。表中3 中的“行”为棋子行坐标;“列”为棋子列坐标;“ S ”为HIS 图像的S 分量图像大于某一阈值的像素点数量;“点”为二值图像细化后,对圆域内亮点的统计数。第1个值代表图5 最上面第1 行的红色棋子“车”,第2个值代表第1行第2个棋子“兵”,……,以此类推。

表2 未经细化所求取的像素数结果
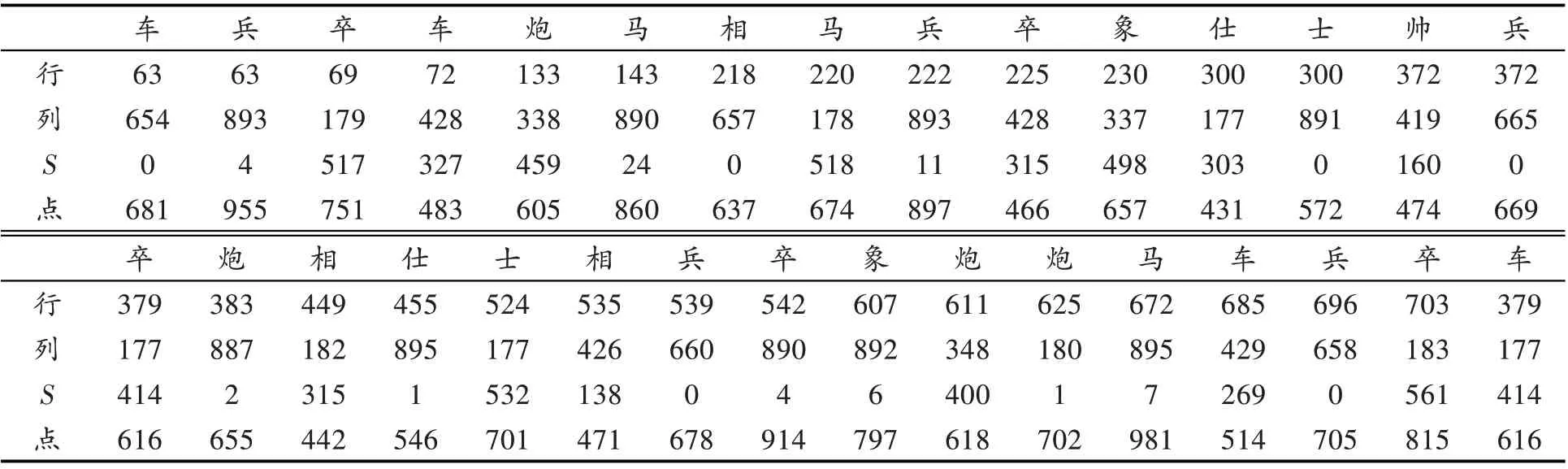
表3 细化后所求取的统计像素的结果
由表中S 值可见,红色“车”的S 值为0,而黑色“车”的S 值为327,所以利用S 分量能够很好地将棋子颜色分开。 S 图像的特征可以正确分析出棋子的颜色。在S 图像中识别出来颜色后,分别对黑色和红色棋子进行分类,提高了识别率。因此采用统计棋子像素的方法获取棋子特征对棋子识别。
4 分类器的选择
在各种识别算法中最简单、计算速度最快的识别方法是线性分类器,线性判别函数是形式最简单的判别函数,它具有计算简单、在一定条件下能实现最优分类的性质,因此得到了广泛应用。在线性分类器的基础上,用分段线性分类器可以实现更为复杂的分类。在实际应用中有很多模式识别问题并不是线性可分的,这时就需要采用非线性分类器。比如当两类样本分布具有多峰性质并互相交错时,简单的线性判别函数往往会带来较大的分类错误。这时,树分类器作为一种分段线性分类器,能有效地应用于这种情况。近邻法[6]也是一种分段线性分类器。分段线性判别函数的极端情况,就是将各类中全部样本都作为“代表点”,这时的决策方法称为近邻法。最初的近邻法是于1968 年由Cover 和Hart 提出的,由于对该方法在理论上分析较为深入,直到现在依然是模式识别非参数法中最重要的方法之一。因此本研究选择了最近邻分类器进行识别。
5 开局初始化算法、流程及实验结果
开局初始化的最大优势是时间充分,同时初始化的正确性,对对弈的整个进程都有决定性的意义,因此必须保证初始化的正确性。所以笔者利用时间充分的条件,设计了开局初始化算法[7-8]。
初始化算法如下:获取到24 位真彩色图像,这里由摄像头采集进来的图像仅仅是数据并不是BMP 格式的图像,故而还要对图像进行一些转换,将所获取的图像数据填充到空白的BMP 格式的图像文件中,从而得到了可处理的BMP 格式图像文件。将BMP 图像作为处理的依据,开始进行信息获取。首先将真彩色图像进行灰度变换获取灰度图像,然后进行RGB 色系到HIS 色系的转换,获取到S 图像。对灰度图像进行仿射变换并进行中值滤波,获取新的灰度图像,对新获得灰度图像进行适当增强,突出棋子前景。对灰度图像进行二值化,使图像中棋子前景和棋盘背景明显地区分开。通过二值化获取到的二值图像含有少量噪声,对含有噪声图像进行去噪处理,消除空穴,同时也能去掉非常大的反光噪声。然后对图像进行填充,得到包含所有棋子的圆域。对所获取的图像进行边缘检测就可以获得仅仅包含棋子圆边界的图像,这样就可以为Hough 变换求取圆心创造良好的条件。通过Hough 变换求取仅仅包含圆心的图像,并对该图像圆心进行归一化处理。对灰度图像采用Ostu 二值化方法进行处理,得到字体细节更为明显的图像,以便细化获取更好的统计结果。通过像素统计可以得到棋子的像素特征向量,从而为识别做好准备。单一的像素点个数作为特征向量,对32 个棋子进行识别难度不算太大,但是对棋子图像的颜色进行分类,可以保证识别的正确性更高。所以,本研究利用获得圆心的图像和图像HIS 中的S 分量图像,进行类似的像素点统计,就可以获得到棋子颜色的信息,从而可以对像素点个数的特征向量在更少的棋子中进行分类。此时就可以使用不变矩对细化图像中分割出来的字体进行分类,进一步提高识别结果的可靠性。开局的初始化算法如图6 所示。
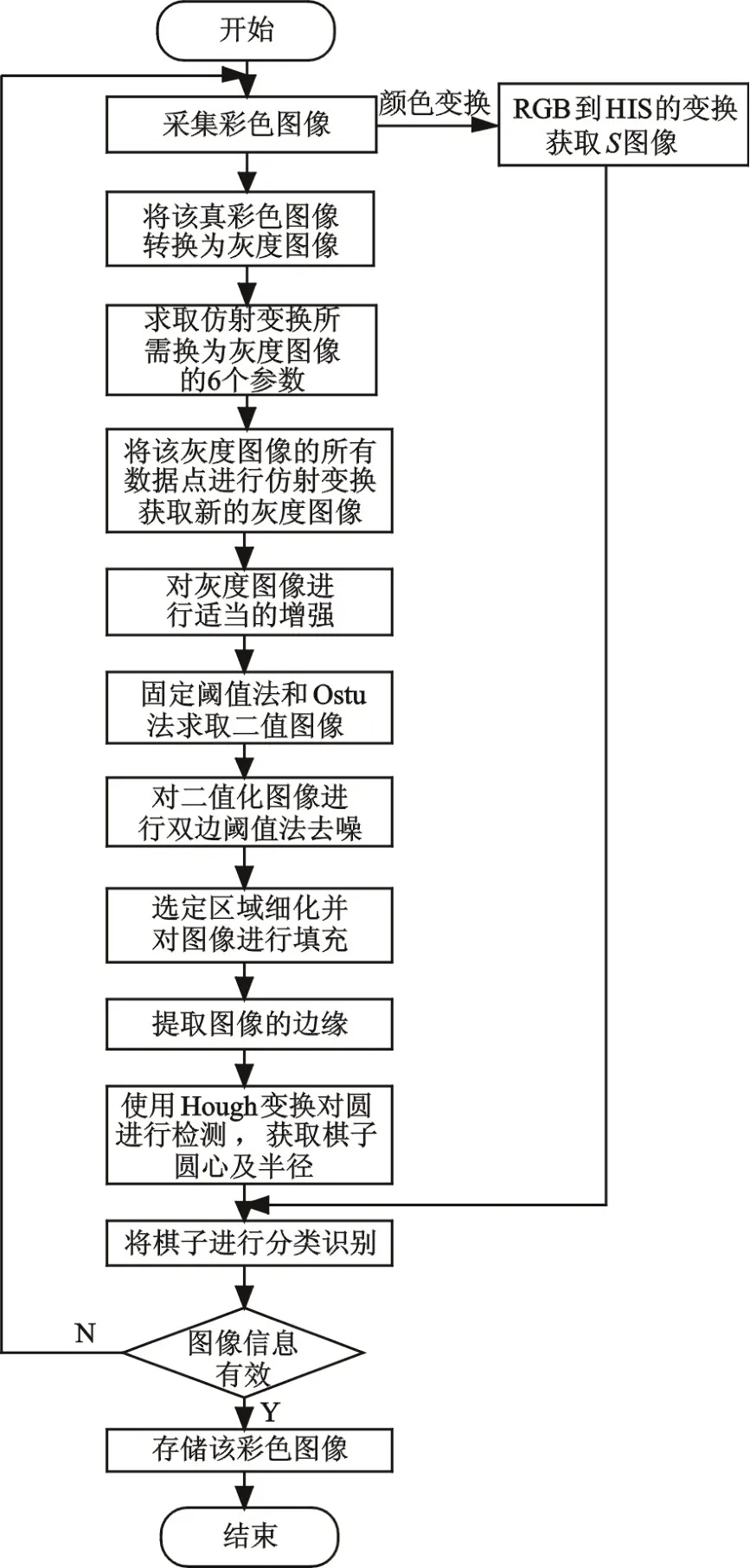
图6 开局的初始化算法
获取棋子的圆形实验结果如图7 所示。

图7 原始图像和求取的圆心坐标
6 对弈进行中算法、流程及实验结果
对弈进行中的算法[9-10]从一定程度上来看是棋局初始化的重复,但不可能完全重复,因为这一过程不具备初始化时的一个重要条件:充裕的运行时间。故而对该算法做出一定的调整是必须的。鉴于此,设计了去掉冗余信息的方法使运行时间缩减,同时又保证了运行的正确性。对弈中算法如图8 所示。

图8 对弈中的算法流程图
对弈中所获取的实验结果如图9 所示。

图9 对弈进行中所获取实验结果
7 棋子识别的算法、流程及实验结果
棋子识别主要利用了两个特征:饱和度和文字像素点数。使用Hough 变换检测到圆心后,即可以对图像S 和图像ImageThin 进行处理,得到棋子红黑特征和文字像素点数两个特征。把棋子区分为红黑特征后,就可以将32 个棋子分到两个域中采用最小距离法进行分类。棋子识别的算法流程如图10 所示。

图10 棋子识别的算法流程图
因为红黑容易区分,故而可以选择在各自颜色范围内进行区分,鉴于图像为理想图像,故而也可以直接进行区分。识别率可达到100 %。如图11和图12 分别是理想棋子和理想棋子旋转后的图像。表4和表5是根据图11和图12计算的结果。

图11 理想棋子图像

图12 旋转后棋子图像
对实际棋盘上的棋子图像进行像素统计,所用的图像是用数码相机获取的图像,原始图像如图5 所示。
S 图像中像素的统计针对棋子圆圈范围内大于某一阈值的像素点进行,通过获取的结果可以清晰地看出,红黑棋子在S 图像中的特征有非常大的区别,很容易区分。获取到棋子的红黑特征后,针对二值图像细化后的结果进行像素统计,其统计结果如表6 所示。
其中表6 中的“行”为棋子行坐标;“列”为棋子列坐标;“ S ”为HIS 图像的S 分量图像大于某一阈值的像素点数量;“点”为二值图像细化后,对圆域内亮点的统计数。
通过表6 中的数据看出,在黑方中,分开卒和炮有一定困难;在红方中,几乎不存在难以区分的棋子。只要对现有棋子进行一些特殊处理,比如炮字体稍微增大等。经过处理后,在分类中便有了较大的选择余地,使用最小距离法便可实现对棋子的正确分类。实验结果表明,该方法的识别率达到98%以上。提高图片的质量后,识别率将会进一步提高。

表4 根据图11 理想棋子像素统计结果

表5 根据图12 棋子旋转后像素统计结果
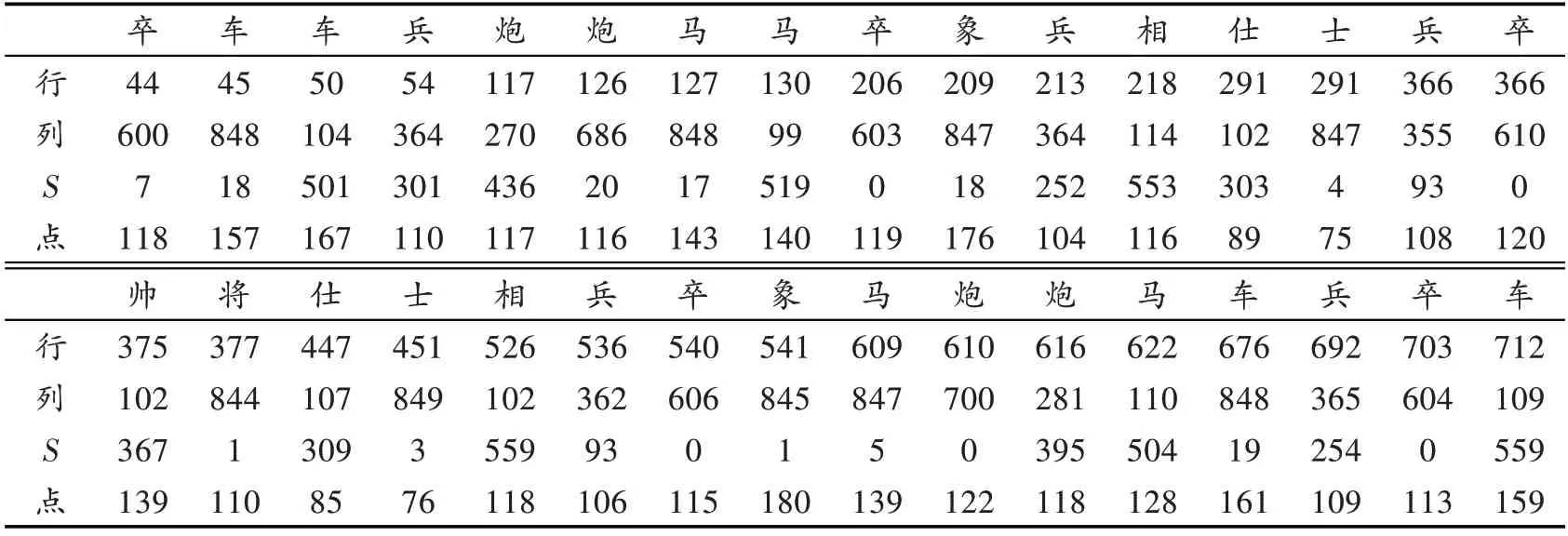
表6 棋子识别结果
8 结语
本研究主要完成了象棋机器人视觉识别算法的研究并给出了实验结果。整个算法流程划分为开局初始化和对弈进行中两个步骤。对棋子进行识别时,使用Hough 变换得到棋子红黑特征和文字像素点数两个特征。把棋子区分为红黑后,就可以将32 个棋子分到两个域中采用最小距离法进行分类,对理想棋子识别的结果表明识别率可以达到100 %,数码相机获得棋盘图像将棋子定位后的识别率为98%以上。
[1] 赵吉文. 基于SVM 的仿人对弈机器人视觉图像处理[J].系统仿真学报,2007,19(18):12-16.
[2] 葛洪央. 机器人运动学的旋量表述[J]. 安徽农业科学,2012,42(10):40-42.
[3] 苏中. 基于激光双目视觉系统的直径测量[J]. 半导体光电,2008,30(1):18-20.
[4] 刘伟. 基于双目立体视觉系统的精确标定算法[J].兵工自动化,2008,29(6):10-12.
[5] 谢妤婵. 视觉目标识别与三维定位关键技术的研究[D].天津:天津大学,2009.
[6] 张祥合. 复杂场景中目标识别与分类的仿生原理和方法[D].吉林:吉林大学,2012.
[7] 时国平. 工业机器人视教盒系统的设计[J]. 兵工自动化,2006,15(5):37-40.
[8] 钟韬. 系统标定中的透视投影模型[J]. 兵工自动化,2011,65(3):24-26.
[9] 朱嘉. 基于视觉与触觉集成传感的多坐标组合测量系统的研究[D].天津:天津大学,2010.
[10]王春丽. 中国象棋嵌入式视觉识别算法和程序开发[D].北京:北方工业大学,2010.

