机床行业产品质量控制的非合作均衡策略研究*——随机微分博弈的视角
于 伟,辛宝贵
(1.天津大学 管理与经济学部,天津 300072;2.天津工业大学 理学院数学系,天津 300387;3.山东科技大学经济管理学院,山东青岛 266590)
0 引言
行业产品质量指的是在商品经济的范畴,该行业依据本行业的产品标准,对行业产品进行相应的规划、设计、制造、检测、计量、运输、储存、销售、售后服务、生态回收等全程的必要的信息披露。随着世界各国对产品质量与安全越来越重视,全社会在产品质量和安全性方面的费用支出额占国民生产总值的比重愈来愈大,约占总销售额的10%;另一方面是质量同整个国家生产率水平的关联,产品或服务质量不仅是当代决定企业素质、企业发展和企业经济实力和企业竞争优势的主要因素,也是决定一国竞争能力和经济实力的主要因素[1-2]。
产品质量都是任何一个国家社会的大事,因为它事关人民生命健康财产安全。近年来,有许多学者开始研究产品质量控制问题。如赵道致和吕昕[3]运用微分博弈方法对企业的产品质量决策问题进行了研究,提出动态环境下两个相互竞争企业之间产品质量决策的分析模型;苏秦等[4]基于产品质量角度,应用客户需求及优化理论,研究了产品质量、价格及交付提前期竞争下的企业最优决策问题;刘小鲁[5]以二级价格歧视模型为基础,通过引入对不同产品种类的非对称价格上限管制讨论了中国药品价格管制背景下厂商的产品质量和产品多样化决策,并由此分析了管制的实际效果;秦利[6]研究发现,农产品协会能够提高政府对产品质量的监管能力,并促使农产品供给者遵循行业标准,既确保了农产品质量安全,也促进了农产品供给者利益最大化。夏珑和史红民[7]研究发现,规制者与被规制者之间的质量博弈过程对产品质量有着重大影响,只要生产质量不合格产品的预期收益大于预期成本,企业就有生产的冲动;谢地和孙志国[8]认为,产品质量监管制度合理与否,关键在于对参与人是否实施了有效的约束和激励,有效的约束和激励能够引导参与人遵守规则,而无效的约束和激励则会收到相反的效果。
本文首先建立了固定时限内机床企业2 与企业1不合格产品投放市场的非合作随机微分博弈模型,接着运用Hamiton-Jacobi-Bellman-Fleming 原理,求出了该博弈模型的反馈纳什均衡解,并提出了其满足子博弈一致性的结论,最后进行了数值模拟,验证了研究结果的正确性。本文的研究结果可以为我国制定机床行业产品质量控制政策提供必要的理论支持。
1 非合作随机微分博弈模型
为了便于建立数学模型,我们将所研究的机床行业仅存在两大寡头:寡头企业1 和寡头企业2。这样,我们可以将博弈参与人i(i =1,2)记作:寡头企业1 为参与人1,寡头企业2 为参与人2。为了明确问题,再做如下假设:
(1)假设qi(t)是博弈参与人i 在时间t ∈[0,T]的产量,ei(t)= hi(qi(t))为参与人i 生产qi(t)的产量时投入市场的未达行业标准的产品数量。记ri(qi(t))为参与人i 生产qi(t)的产量时的净收入,即总收入减去总成本。
(2)假定hi(qi(t))是严格递增的函数,即(hi(qi(t)))>0,所以,我们可以记ri(qi(t))=ri(ei(t)),为了进一步简化符号表示形式,记Ri(ei(t))= ri(ei(t))。
(3)假定Ri(ei(t))是关于ei(t)递增的凹函数,即R'i(ei)≥0,R”
i(ei)≥0,Ri(0)= 0。Di(s(t))是治理成本函数,表示未达行业标准产品的市场存量为s(t)时,消费者因担心购买到不合格产品采取避免或减少消费该行业产品而给参与人i 产生的损失,是单调递增的凸函数。
(4)令s(t)为未达行业标准产品的市场存量,它的变化依赖于两个寡头企业对未达行业标准产品的投放水平。μ ≥0 为常数,表示两个参与人投放未达行业标准产品的边际影响,ε >0 为常数,表示未达行业标准产品的市场存量的自然损耗率,为了便于数学处理,不失一般性,我们假设投放未达行业标准产品的边际影响对两个参与人是相同的。σ ≥0 为常数,表示不可预知的因素的影响,W(t)是维纳过程。
(5)假定博弈结束时间T 时的收益为gs2。
(6)假定博弈双方在没有达成一致协议的情况下,参与人i 会单独采取行动以实现自己的期望收益最大化的目标。
根据以上假设,我们可以得到固定期限内两寡头企业将未达行业标准产品投放到市场问题的非合作随机微分博弈模型,如下所示:


其中,s0表示初始时刻t = 0 时的未达行业标准产品的市场存量,ds(t)表示未达行业标准产品的市场存量的变化,r 为贴现率,e-rt是贴现因子。
我们把式(1)与式(2)构成的非合作随机微分博弈记为Γ(s0,T-0)。把与式(1)与式(2)结构一样,开始时间为τ ∈[0,T),开始状态s(τ)= sτ∈S 的非合作随机微分博弈记为Γ(sτ,T-τ)。
2 模型的求解


为了在数学易于处理我们假设净收入函数Ri(ei),i = 1,2 是未达行业标准产品的市场投放量ei(t),i =1,2 的二次函数,治理成本函数Di(s(t)),i =1,2 是未达行业标准产品的市场存量s(t)的二次函数。
为了便于数学处理,同文献[8]类似,我们假设:

其中αi>0 为常数,βi≥0 为常数,注意到参与人面临不同的收入和成本参数,假定成本参数β2≥β1≥0。则参与人i = 1,2 的期望收益(支付)的目标函数为:
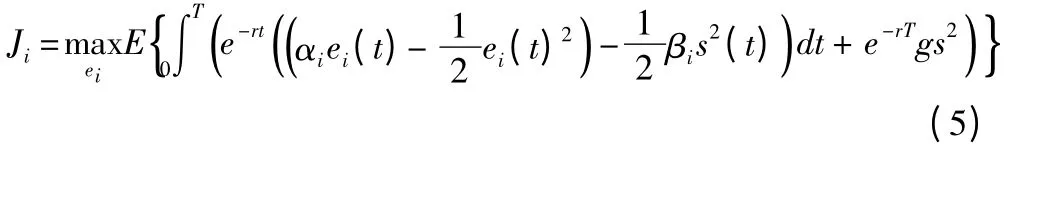
则参与人i = 1,2 按照式(4)和式(5)最大化自己的期望收益(支付):
根据引理3.1,我们可以得到:
定理3.2 对非合作博弈式(4)和式(5),博弈的参与人i = 1,2 的反馈纳什均衡解为:

其中,Ai(t),Bi(t),Ci(t)满足:
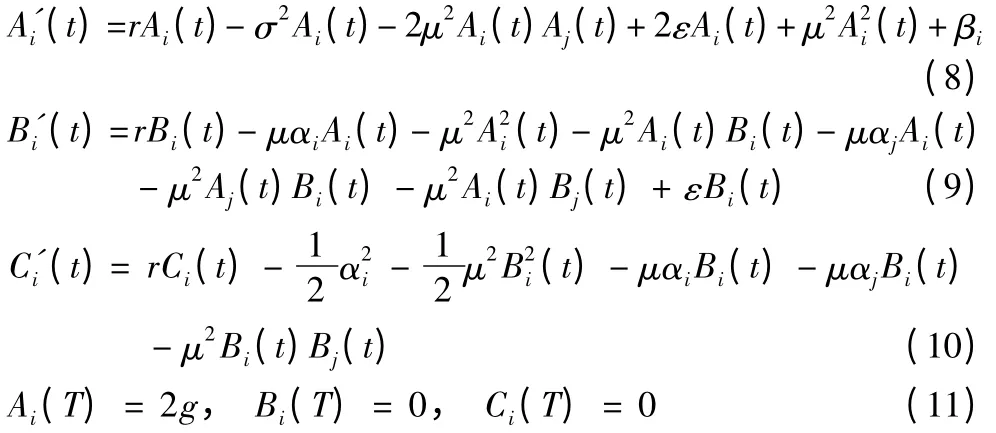
说明:由定理3.2 中ei(t),ej(t)的表达式知道,反馈纳什均衡策略ei(t),ej(t)和当前时间t 和状态s有关,与状态s 的初始值s0无关,所以,反馈策略ei(t),ej(t)是马尔科夫的[10]。
定义3.2 在非合作随机微分博弈Γ(sτ,T-τ)所构成的纳什均衡解中,参与人i,i = 1,2 的价值函数(t,st),i = 1,2,即当状态变量为s(t)= st时,参与人i,i = 1,2 在区间[t,T]上的期望支付的现值为:

对于τ ∈[0,T),t ∈[τ,T),i = 1,2。
根据定义3.1,我们有
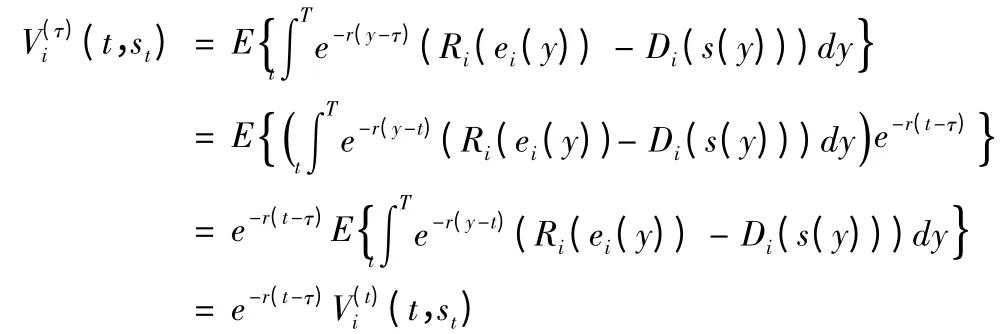
性质:在区间[τ,T]上的非合作随机微分博弈Γ(sτ,T-τ),当状态变量为s(t)= st时,参与人i =1,2 在区间[t,T]上的期望收益的现值等于它的子博弈的值函数进行相应的贴现值,即满足子博弈一致性,当非合作博弈沿着最优轨迹进行,参与人总会根据最初的最优共识原则,都不愿意偏离一直采用的“最优”行为。
3 数值仿真
为了便于进行数值模拟,我们固定以下参数:r =0.05,ε = 0.1,β1= 0.2,β2= 0.4,σ = 0.1,α1= 2,α2= 2,μ =0.6;取如下初值:A1(1)=0.3,B1(1)=0.6,C1(1)= 0.1,A2(1)= 0.2,B2(1)= 0.4,C2(1)=0.1;取步长h = 0.01,取博弈的固定期限T = 50。
机床企业1,如图1 所示,其期望收益V1随未达行业标准产品的市场投放量e1的增大而增大,未达行业标准产品的市场存量s 也随未达行业标准产品的市场投放量e1的增加而增加。

图1 企业1 未达行业标准产品的市场投放量e1、期望收益V1 和未达行业标准产品的市场存量s 之间的关系
机床企业2 的未达行业标准产品的市场投放量及其期望收益与未达行业标准产品的市场存量之间的关系同企业1 的非常类似,如图2 所示,其期望收益V2随未达行业标准产品的市场投放量e2的增大而增大,未达行业标准产品的市场存量s 也随未达行业标准产品的市场投放量e2的增加而增加。

图2 企业2 未达行业标准产品的市场投放量e2、期望收益V2 和和未达行业标准产品的市场存量s 之间的关系
4 结论
(1)不论机床企业1 还是企业2,都非常重视本企业的产量质量控制问题,并且也需要花费大量的时间和费用成本。以往的研究,要么是从实证分析出发,调查利益相关者的未达行业标准产品的市场投放量,做出一个静态的产品质量控制决策,要么是运用微分博弈的等确定性的方法,不考虑随机因素的影响,做出一个确定性的产品质量控制决策。本文考虑到不确定性因素的影响,运用随机微分博弈理论作为解决不确定性动态决策的有效工具,构建机床行业产品质量控制的非合作随机微分博弈模型,并计算出了该模型的反馈纳什均衡策略(反馈纳什均衡解)。指出该模型的反馈纳什均衡策略e1(t)和e2(t)与当前时间t 和状态s 有关,与状态s 的初始值s0无关,也就是说,该模型的反馈策略e1(t)和e2(t)是马尔科夫的。
(2)非合作均衡策略的性质:在区间[τ,T]上的非合作随机微分博弈Γ(sτ,T-τ),当状态变量为s(t)= st时,参与人i=1,2 在区间[t,T]上的 期望支付的现值,等于它的子博弈的值函数进行相应的贴现值,即满足子博弈一致性。
(3)在机床行业产品的质量控制问题上,机床企业1 和企业2 都会理性地选择模型的均衡解作为本企业质量控制的最优策略。
[1]张世煜. 我国产品质量安全监督管理[M]. 北京:中国计量出版社,2012.
[2]郑红军. 中国产品质量的综观研究[M]. 北京:中国经济出版社,2007.
[3]赵道致,吕昕. 动态竞争环境下企业产品质量决策研究[J]. 组合机床与自动化加工技术,2011(3):89-92.
[4]苏秦,李永飞,郑婧. 产品质量价格及提前期竞争下的企业最优决策[J]. 工业工程与管理,2011,16(5):1-8.
[5]刘小鲁. 产品多样化、产品质量与中国药品价格管制绩效[J]. 经济评论,2010(6):76-84.
[6]秦利. 农产品协会产品质量安全控制行为的模型分析[J].世界农业,2010(12):49-52.
[7]夏珑,史红民. 规制博弈与产品质量[J]. 企业经济,2010(2):46-50.
[8]谢地,孙志国. 监管博弈与监管制度有效性[J]. 产品质量监管的法经济学视角,2010(2):175-177.
[9]杨荣基,彼得罗相,李颂志. 动态合作——尖端博弈论[M]. 北京:中国市场出版社,2007.
[10]Basar T,Olsder G. Dynamic non-cooperative game theory(2nd ed)[M]. New York:Academic Press,1995.

