基于Wien 桥的混沌保密通信系统设计*

吕恩胜 ，黄双成

(河南化工职业学院机械电子系，郑州450042)

混沌现象的研究已成为当今诸多科学研究领域的热点问题之一［1-3］。混沌同步与控制是混沌系统的重要概念，混沌保密通信是混沌电路的重要应用。正弦波振荡电路是电子技术中的一种基本电路，它在通信、控制等许多领域有着广泛的应用［4］。本文以Wien 桥振荡器和滞回比较器为基础，构建混沌电路，并以该混沌电路设计混沌保密通信系统。

1 Wien 桥振荡电路与滞回比较器

1.1 Wien 桥振荡电路

图1 为Wien 桥式振荡器，电容C1、C2两端电压为u1、u2，反相输入端电压为u3。理想运算放大器工作在线性区，“虚短”“虚断”特性成立，可知u1=u3，i+=i-=0，设R2=R3=R，C1=C2=C。

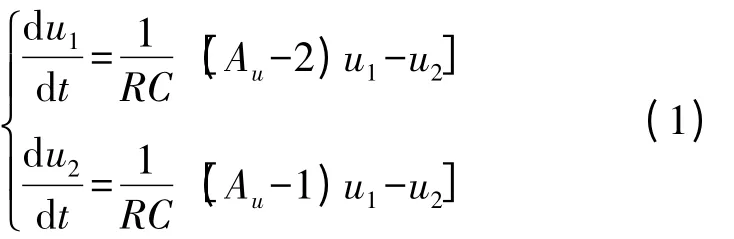
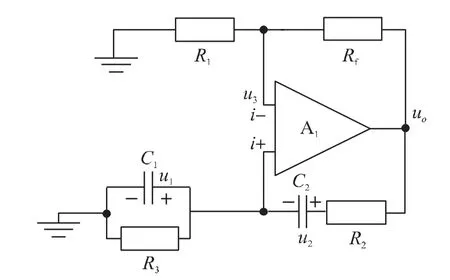
图1 Wien 桥振荡电路

式(1)中，Au=1+Rf/R1，为文氏电桥振荡电路的闭环增益。

由式(1)和式(2)消去u1、u2，输出电压uo为变量的电路方程为

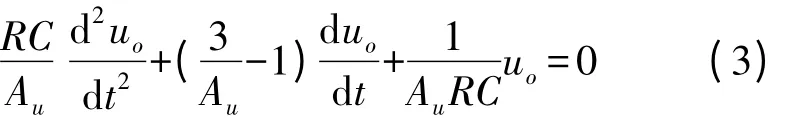
分析式(3)，Au=3 是电路响应uo输出为正弦波的条件。但是，外界干扰使得元器件性能发生变化，Au=3时，输出的正弦波不是稳定的。当R1、Rf的变化使得Au＜3，式(3)的特征根在复平面的左半部分，响应输出的振荡波形是衰减的;同样，当Au＞3，式(3)的特征根在复平面的右半部分，响应将输出的振荡波形是发散的。这个系统在本质是一个线性系统，它只有一个平衡原点，Au＞3 时，原点不稳定，Au＜3 原点全局吸引且稳定。当Au∈(1，5)时，系统为螺旋的，Au→±∞时，λ1→±0，λ2→∞。系统能产生振荡信号，是电容电压受限于电源电压而产生的一个稳定的极限环［5-6］。

1.2 滞回比较器

1.2.1 阈值电压

理想的集成运放，正负饱和输出电压绝对值大小相等，差模增益为无穷大，图2(a)所示滞回比较器只引入正反馈，因此输出电压uo有两种状态，不是高电平UOH，就是低电平UOL，设UOH=-UOL=UZ，那么uo=±UZ。集成运放反相输入端电位uN=ui，同相输入电位

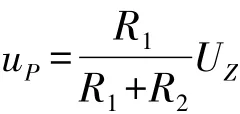
令uN=uP，求出阈值电压

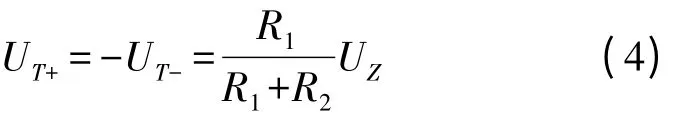
1.2.2 工作原理及电压传输特性

设ui＜UT-，则uN＜uP，uO=+UZ。此时uP=UT+，增大ui，直至UT+，再增大，uO才从+UZ跃变为-UZ;设ui＞UT+，则uN＞uP，uO=-UZ。此时uP=UT-，减小ui，直至UT-，再减小，uO才从-UZ跃变为+UZ。图2(b)为滞回电路传输特性图。

(2)聘用兼职。通过各种途径聘用从事本专业相关工作、具有丰富实践经验的工程技术人员、技术工人担任兼职教师，专门化方向课程的教学可以由校企合作办学的企业方工程技术人员承担。

2 混沌电路设计

2.1 电路描述

在文献［5-6］中设计出的Wien 桥混沌电路，其所用Wien 桥电路如图2 所示，连接电容C1、C2之间的信道在理想状态下电阻为零是没有压降的，混沌保密通信的载波信号是电压，因此文献［5-6］的电路不适用于混沌调制保密通信。本文设计的混沌电路是在文献［5-6］的电路基础上进行修改，在两个电容C1、C2之间增加一个耦合电阻R 产生压降。图3 网络N1为修改后的Wien 桥振荡电路，图3 网络N2为滞回电路。电路把电容C1和电阻R 上的电压输出给滞回电路，滞回电路的输出电平uo在±UZ二者中切换，然后又输出给前者，这个过程周而复始循环，电路产生混沌。

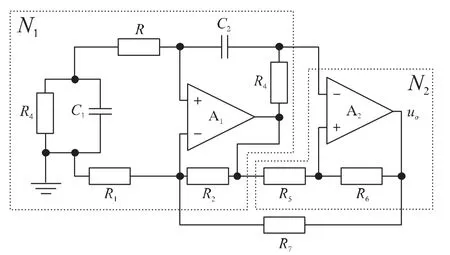
图3 Wien 桥混沌电路

2.2 混沌系统方程

设电容C1为电压为u1，电容C2电压为u2，C1=C2=C，电阻R 的电压为uR，两个集成运放为理想的，滞回比较器输出为uo，根据电路的KCL，KVL 定律，图3 得到的系统方程为:

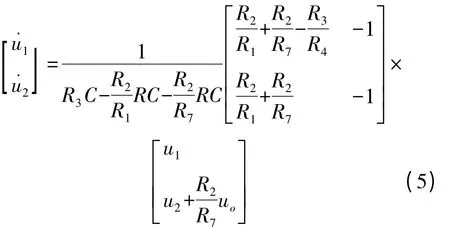
其中uo=±UZ。

滞回比较器的阈值电压

通过改变改变R5，R6，R7的阻值，从而改变阈值电压UT+、UT-，为了使系统起振，式(5)特征根必须为实部正的共轭复数，从0 开始调节R6/(R5+R6)系统将会产生混沌。

2.3 混沌电路系统仿真

对Wien 桥混沌电路仿真，图3 电路各元器件取值如下:R1=1.8 kΩ，C1=C2=10 nF，R3=R4=3 kΩ，R2=3.9 kΩ，R5=3.3 kΩ，R6=19.6 kΩ，R7=46.8 kΩ，R 在选取阻值时，不宜过大，过大Wien 桥振荡电路不能输出正弦波;过小R 上压降太小而不能后文的混沌调制通信的载波信号，取R=0.05 kΩ，图4为EWB 仿真的Wien 桥混沌电路的系统轨迹相图。

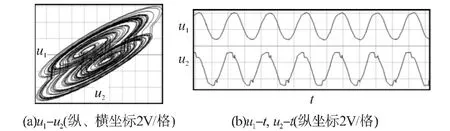
图4 Wien 桥混沌电路的系统轨迹相图

3 混沌保密通信设计

3.1 混沌调制通信技术

混沌调制通信是一种典型的模拟保密通信方式，其原理如图5 所示，发送端和接收端结构完全相同，发送端具有近似高斯白噪声统计特性的混沌载波信号x(t)与调制信号m(t)相叠加，形成混沌调制信号s(t);接收端，用带有调制信号的混沌载波信号s(t)减同步的混沌信号x'(t)，解调出的信号m'(t)。混沌系统同步决定了混沌调制通信，被加密信号m(t)的幅度都很小，为了混沌信号不偏离原本的混沌轨道，通常x(t)的功率比m(t)的功率大很多。

3.2 混沌保密通信系统设计

混沌系统的演化对初始条件十分敏感，并且出现类似噪声的行为，因此混沌电路运动形态的最大特点是不可预测性，故适用于保密通信系统。以Wien 桥混沌电路为例，设计由自由混沌到混沌同步最后出现混沌保密通信的演变。

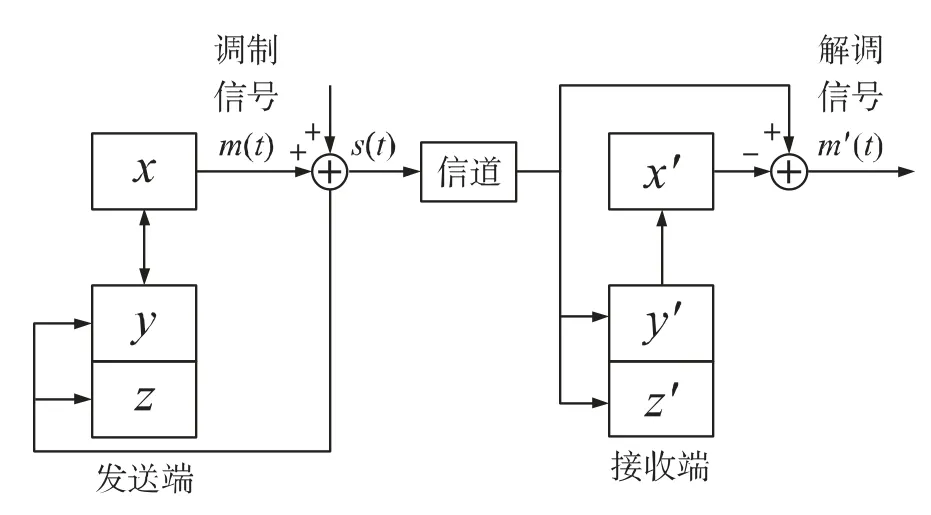
图5 一种混沌调制单向保密通信原理图

以图3 为电路例，应用混沌调制通信技术，设计保密通信系统。电阻R，左边连接C1、R4组合的并联电路，右边连接C2、R3组合的串联电路，是两边电容C1、C2的电压u1与u2的耦合通路，R 两端的信号互相传送，方向相反，将两个方向信号的传送分开，得到调制载波和解调载波。设计方案是:如图6网络N1(发送端)所示，对于自左向右的信号用电压跟随器A3和电阻Ri串联，取代电阻R;对于自右向左耦合方向的信号用电压跟随器A4、两级反向放大电路(A5、A6)和电阻R'i串联，取代电阻R，其中第一级反向电路A5改为第一级反向加法放大电路，反向加法放大电路的另一个输入端加入调制信号ui，从而实现了Wien 桥混沌电路对调制信号的加密;网络N2(接收端)中，对电路进行控制，相反的解密运算得到解调信号uo。

图6 中，将N1部分和N2部分通过信道连接在一起，构成了两个Wien 桥混沌电路的同步，并且实现通信。各元器件取值如下:R1=R13=1.8 kΩ，C1=C2=C3=C4=10 nF，R2=R14=3. 9 kΩ，Ri=R'i=Ro=R'o=0.05 kΩ，R3=R4=R15=R16=3 kΩ，R8=R9=R10=R11=R12=R20=R21=R22=R23=R24=R25=R26=10 kΩ，R5=R17=3.3 kΩ，R6=R18=19.6 kΩ，R7=R19=46.8 kΩ。图7 为EWB 仿真的调制信号ui和解调信号的uo波形，结果可知，调制信号与解调信号的波形相同，因此该电路适用于保密通信。在该电路中，由于发送端调制信号ui，被Wien 桥混沌电路产生的混沌信号所调制，被调制信号具有混沌的随机性，窃听者要想获取有用信号只有他的电路与发送端的电路完全相同且同步，这在技术难度较大，因此该保密通信电路具的保密性能很好。

图6 完整的Wien 桥混沌电路保密通信系统

图7 Wien 桥混沌保密通信电路的收、发调制信号(纵坐标10 mV/格)

4 结论

本文设计出Wien 桥混沌电路，该电路的主要特点是，结构简单，性能稳定。以该混沌电路设计的混沌保密通信系统方案，计算机仿真结果:可实现发送端与接收端之的通信且同步，接收端的解调信号与发送端的调制信号一致，表明该方案有效。

［1］ Pecora L M，Carroll T L.Synchronization in Chaotic Systems［J］.Physics Review Leters，1990，64(8):821-824.

［2］ 吕金虎，陈关荣.混沌控制与反控制:机遇与挑战［J］. 科学观察，2006，1(6):39-39.

［3］ 吕恩胜，裴东.一种新的图像保密通信系统设计［J］.微型机与应用，2010，29(9):35-37.

［4］ 华成英，童诗白.模拟电子技术基础(第四版)［M］.北京:高等教育出版社，2006.

［5］ Li Q，Yang X S.Chaotity Wien-Brige Harmonic Oscillators［C］//IEEE Proceeding of ICCCAS’06，2006，2361-2364.

［6］ 李清都. 混沌系统分析与电路设计［D］. 武汉:华中科技大学，2008.

［7］ 杜桂芳，张新国.EWB 仿真混沌保密通信电路［J］. 甘肃科技，2006，22(3):75-76.