基于压缩感知的模拟LFM信号采集

舒奇泉，贾 鑫

（1、装备学院研究生院，北京101416；2、装备学院光电装备系，北京101416）

0 引言

现代雷达信号带宽越来越宽，频率越来越高，前端采样受Nyquist采样定理限制，硬件实现越来越困难。压缩感知理论（CS）［1-2］指出，对于稀疏信号，可以突破Nyquist限制，以较小的采样率得到较少的采样值并精确重构信号。这样，采样率的要求由信号的信息量大小确定，而不是简单地由信号频率确定。在现有硬件的基础上，引入压缩感知理论，可以以较小的采样率采集模拟LFM 信号，经过数字化重构，得到数字信号以进行其他处理。经过研究分析，压缩感知理论对信号处理有良好的性能，对模拟信号的处理也可以实现。Matlab 仿真分析表明，基于压缩感知的模拟LFM 信号采集系统突破了前端采样Nyquist极限，具有较小的采样率和较好的重构精度。

本文首先分析了压缩感知基本原理和实现方式，然后通过理论推导分析基于压缩感知的模拟信号处理方法，最后通过Matlab进行仿真验证。

1 基本原理分析

LFM 信号因其大时宽带宽积的优良特性在雷达领域受到广泛的应用［3］。典型的LFM 信号为：

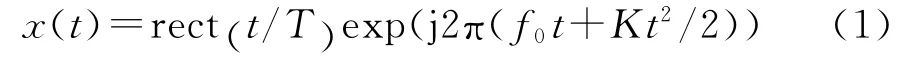
式中，T 为脉冲宽度，f0为起始频率，B 为信号带宽，K＝B／T 为调频斜率。传统采样时，对模拟信号经过下变频、滤波等操作后再经过ADC 可以转换为数字信号。依据Nyquist采样定理，对LFM 模拟信号采样时，ADC采样率fs至少为2B，才能无失真恢复信号。

2006年，Candes等公开发表了多篇关于压缩感知基本理论的论文，为该理论奠定了基础［1-2］。其数学描述如下：

设一维离散时间信号X 为RN空间的N×1维列向量，其分量为X（n）（n＝1，2，…，N）。把X 表示成为RN空间 上 的 一 组N×1 维 基 向 量的 线 性 组合，系数为αi（i＝1，2，…，N），其数学表达式为：

式中，Ψ 为基向量构成的矩阵，α 为系数组成的N×1维列向量，它与X 是同一个信号的等价表示方式。设计一个平稳的、与变换基Ψ 不相关的观测矩阵Φ（M×N），对原始信号X 进行观测，得到观测值Y 为ΦX，即Φψα，定义CS信息算子ACS为Φψ，则观测值Y 等于ACSα，为信号X 通过ACS进行非自适应观测的结果，且Y 的维数为M。信号重构时，要从得到的维度为M的观测值中求解维数为N 的X，M＜N，通常意义上无法求解。理论证明，在满足限制等距性（RIP）［4］的条件下，可以利用线性规划求出最优解。利用0-范数意义下的优化问题求解X：

RIP准则数学定义为：

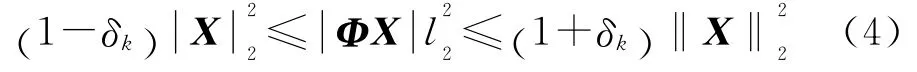
理论指出，要应用压缩感知，信号要具有稀疏性，或者在某个确定的域里面稀疏。信号稀疏性可定义为：

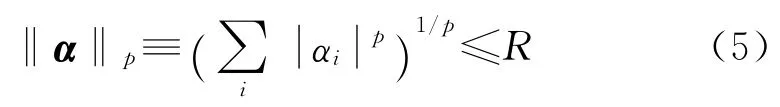
满足式（5）的系数向量α 在某种意义下是稀疏的。常见自然信号往往不是标准的稀疏信号，需要用变换基进行稀疏表示。为了能够更好地稀疏表示信号，文献［5］提出了基于正交基字典的稀疏表示方法。即在由多个正交基构成的树形正交基字典中自适应地寻找信号的最优正交基，对信号进行变换以得到信号的最稀疏表示。

2 基于压缩感知的模拟信号处理

以上压缩感知处理方法均是矩阵运算，难以硬件实现。为此，有学者提出了新的信号处理结构：宽带调制转换器（MWC）［6-7］，把压缩感知理论应用到模拟信号处理领域，实现在采样的同时压缩数据，不但可以降低采样率，也可以减少数据量，降低采样系统的存储要求，因此受到了极大关注。

2.1 MWC系统采样

MWC系统实现框图如图1所示。输入的模拟信号最大频率为fmax，共含有N个宽度不超过B 的子频带。系统前端由不同的m个信道输入信号，每个信道中的信号x（t）与周期为T 的波形p（t）相乘，再分别经过截止频率为1／（2T）的低通滤波器进行滤波，然后以1／T 的速率进行低速采样，得到各个频段内的采样值，用于信号的重建。

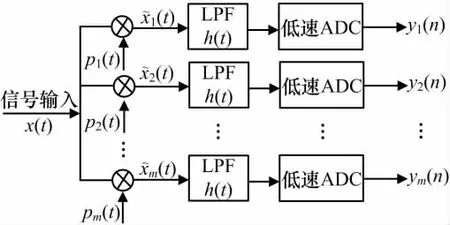
图1 MWC系统实现框图

混合函数p（t）具有周期性，每个周期内以伯努利分布随机取值M个±1，M 即代表了降采样率。时域模型可以表示为：

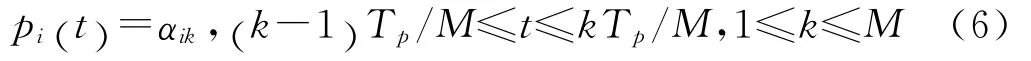
式中，αik为｛1 -1｝ 。同时，可以得到周期函数pi（t）的傅里叶变换Pi（t）为：

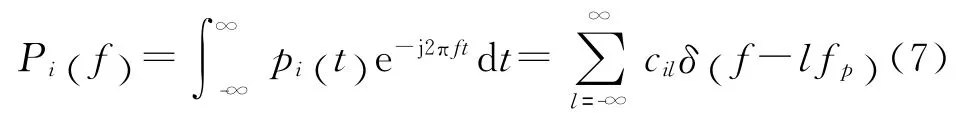
式中，cil表示混合信号的傅里叶系数：

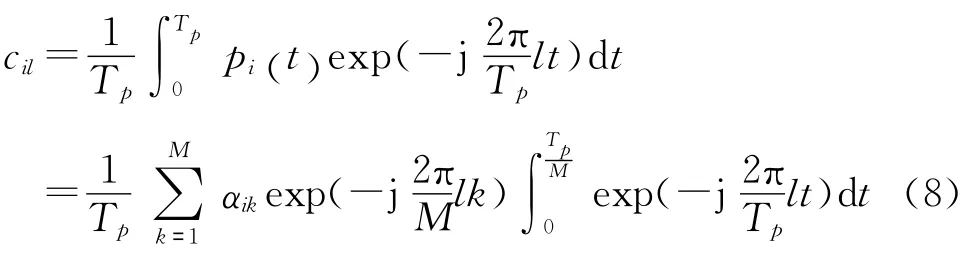
信号与混合函数相乘再通过传递函数为H（f）的理想低通滤波器，然后以fs为采样率进行低速采样得到输出yi（n），其DTFT 分别可以表示为：

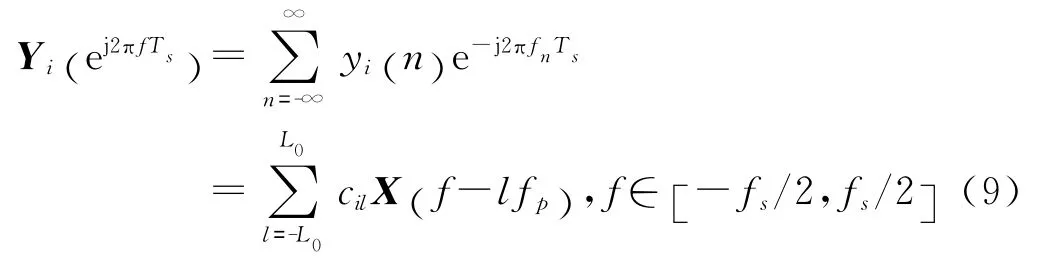
式中，L0的选取标准为：

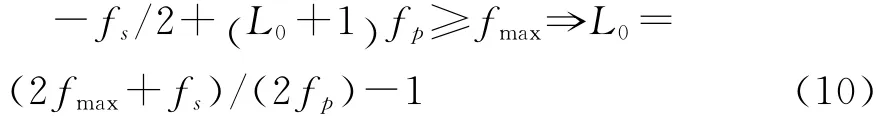
考虑式（9）的矩阵形式，可以写为：

式中，y（f）和z（f）分别为m 维和L（即2L0＋1）维的向量，向量元素为：

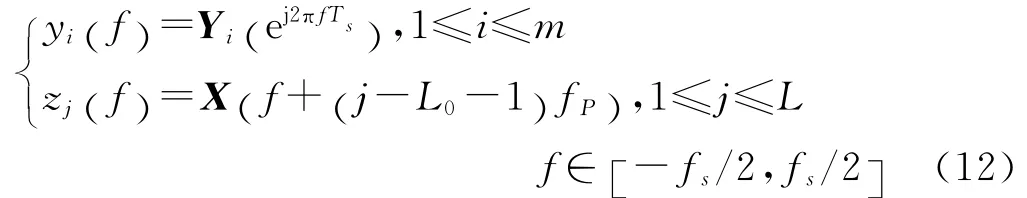
而矩阵A 为维m×L，元素为系数cil：

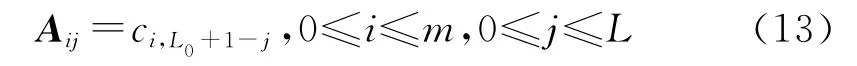
观察式（2）与式（11）可知，其形式相同，可利用压缩感知理论解出式（11），重构出原信号。

2.2 MWC系统信号重构

从得到的采样值中恢复原信号，MWC 重构模块结构图如图2所示。

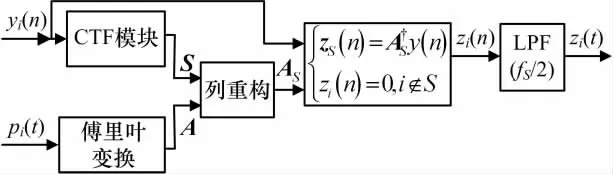
图2 MWC系统重构模块

由于得到的是连续采样值，需要转化为离散矩阵形式便于计算，此过程由连续到有限（CTF）模块［6］完成，其结构如图3所示。

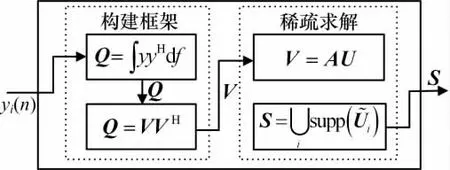
图3 CTF模块结构示意图

CTF首先建立测量值的框架V。在采样时间nTs时，得到采样值向量为y（n）＝［y1（n），y2（n），…，ym（n）］T，以此构造矩阵Q，表达式为：

在实际采样中，一般只需要n＝2m 即可。然后对矩阵进行分解Q＝VVH，得到框架V。

此时可以利用OMP 等稀疏重构算法求解V＝AU，得到最稀疏矩阵~U，进一步得到信号支撑集S：

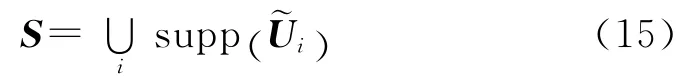
由S 求得AS，即取出A 中对应S 所在的列构成新矩阵。在（12）式中，对zi（f）做IDTFT得到zi（n），则：

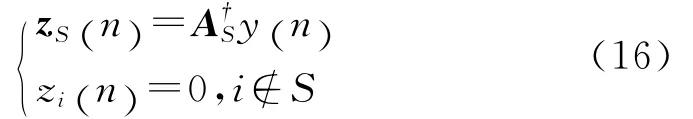
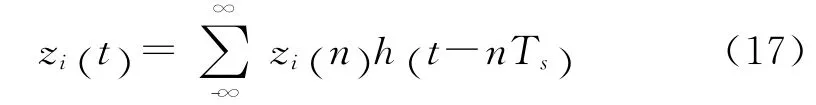
式中 h （t） ＝sinc（ πt ／Ts），经 过 调 制 得 到 重 构 模 拟信号：

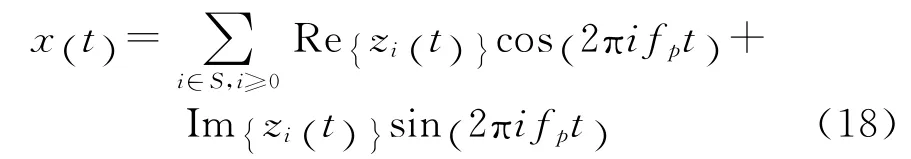
研究表明，WMC适用于高频率、多个窄带的频域稀疏信号［8］。文献［9］指出了MWC 可以处理的信号有通信信号（包括跳频信号、载频未知且在较大范围内随机出现的信号）、音频信号、缓慢变化的Chirp信号（雷达信号、地震波信号）、平滑信号（只需要少量的傅里叶系数进行表示）、分段平滑信号等。

3 仿真实验

Matlab仿真设置参数如下：LFM 信号带宽B＝60MHz，脉冲宽度T＝-2μs，调频斜率K＝3×1013，分别设置不同的初始频率和噪声环境，使用MWC 系统直接进行采样，单个通道采样率fs＝50MHz，得到测量值然后用OMP算法重构信号。

3.1 初始频率为0的无噪声信号重构

图4、5分别表示了在初始频率设置为0 的情况下，重构信号与原信号在时域、频域（经过放大）的对比。可以看出，重构误差都比较小，实现了以低于Nyquist采样率对LFM 信号的采样。

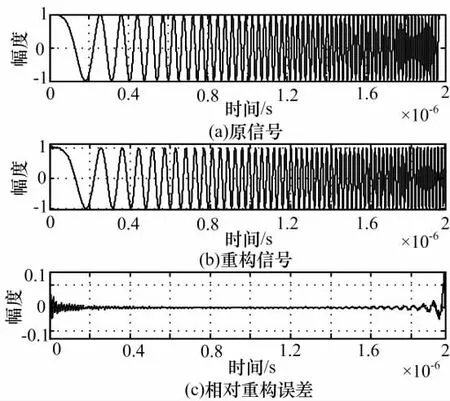
图4 初始频率为0时信号重构时域对比

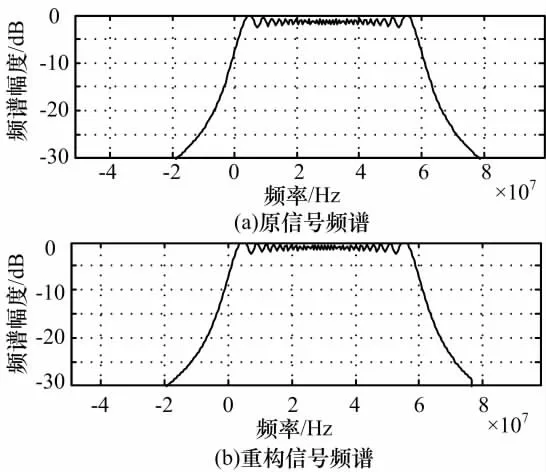
图5 初始频率为0时信号重构频域对比

3.2 初始频率为2GHz的无噪声信号重构

图6、7 分别表示了在初始频率设置为2GHz的情况下，重构信号与原信号在时域（局部）、频域（经过放大）的对比。此时，频率范围为2～2.06GHz，仍然使用单个通道50MHz的采样频率直接进行采样，仿真结果可以看出，重构相对误差也比较小。频域对比也说明了采样的有效性。这表明，利用压缩感知原理，可以实现以较小的采样率对高频率的LFM 信号直接进行采样并准确重构原信号。

图6 初始频率为2GHz时信号重构时域对比

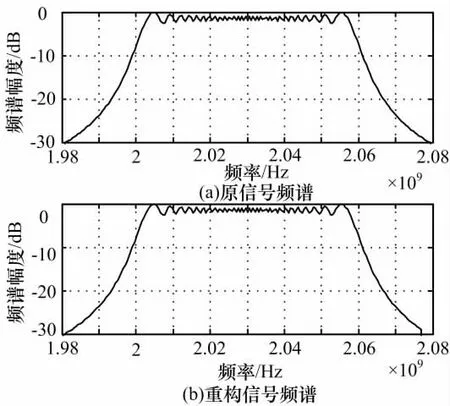
图7 初始频率为2GHz时信号重构频域对比

3.3 初始频率为0的含噪声信号重构

加入随机噪声，设置输入信噪比为15dB，初始频率设置为0，仿真结果如图8、9所示。可以看出，时域重构信号相对原信号误差较小，波形上要明显优于含噪声信号，计算其信噪比可以得出SNR＝15.769dB，比原含噪声信号有所提高，说明MWC 系统有一定的噪声抑制功能，具有鲁棒性。

图8 含噪声LFM 信号重构时域对比

在硬件实现上，高速随机序列的产生可以使用线性移位寄存器，现行硬件可以产生频率高达80Gb／s的随机序列［10］，完全满足采样的频率要求。随后使用常规的模拟滤波器和低速ADC 就可以完成高频率信号的低速采样。综合可见，基于压缩感知的模拟LFM信号采集理论可行，硬件上也可以实现。

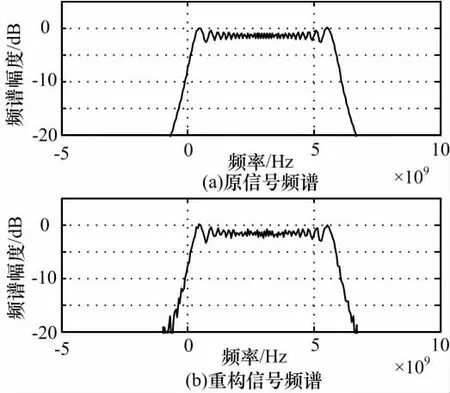
图9 含噪声LFM 信号重构频域对比

4 结束语

根据压缩感知基本原理，通过理论分析与仿真研究，验证了压缩感知理论应用到模拟信号处理中的可行性和优越性。针对现代雷达LFM 信号带宽越来越宽、常规采样受Nyquist采样定理限制使得硬件实现困难的问题，应用压缩感知原理，以较低的采样率实现信号的数字化采集和压缩，从而突破了Nyquist极限。分析和仿真表明，基于压缩感知的模拟LFM 信号采集系统具有较好的性能和可实现性。下一步，需要研究在大带宽、频率快速变化的情况下，提高压缩感知信号重构的性能。同时，需要改进MWC系统，减少通道数，简化硬件实现。■

［1］Candes EJ.Compressive sampling［J］.Proceedings of the International Congress of Mathematicians，2006（3）：1433-1452.

［2］CandesEJ，Romberg J，Tao T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans.on Information Theory，2006，52（2）：489-509.

［3］Mark AR.雷达信号处理基础［M］.刑孟道，王彤，李真芳，译.北京：电子工业出版社，2008.

［4］Candes E.The restricted isometry property and its implications for compressed sensing ［J］.Comptes rendus.Mathematique，2008，346（10）：589-592.

［5］Peyre G.Best basis compressed sensing［J］.IEEE Trans.on Signal Processing，2010，58（5）：2613-2622.

［6］Mishali M，Eldar YC.Blind multi-band signal resconstruction：Compressed Sensing for Analog Signals［J］.IEEE Trans.on Signal Process，2009，57（30）：993-1009.

［7］Eldar YC.Compressed sensing of analog signals［R］.Israel：Department of Electrical Engineering，Technion-Israel Institution of Technology，2008.

［8］Mishali M，Eldar YC.From theory to practice：sub-Nyquist sampling of sparse wideband analog signals［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：375-391.

［9］Tropp J，Laska J，Duade M，et al.Beyond Nyquist：efficient sampling of sparse bandlimited signals［J］.IEEE Trans.on Information Theory，2010，56（1）：520-544.

［10］Dickson TO，Laskin E，Khalid I，et al.An80Gb／s pseudorandom binary generator in SiGe BiCMOS technology［J］.IEEE Solid-State Circuits，2005，40（12）：2735-2745.