钢芯铝绞导线的微动疲劳及其寿命预测
陈国宏,倪满生,刘俊建
安徽省电力科学研究院材料工程研究所,安徽合肥,230601
微动疲劳是疲劳和微动磨损协同作用导致的损伤过程。一般认为,风致振动导致导线内部股线之间、导线与线夹之间的微幅滑移和交变应力,由此产生的微动磨损,继而引发疲劳裂纹的萌生和扩展是导线损伤、导线使用寿命降低的主要原因[1]。开展微风振动下架空导线的运行状态评估及其剩余寿命预测,有利于加强对架空导线运行的管理,保障供电安全。
1 ACSR导线的微动疲劳
1.1 试验内容
选用LGJ150/20型钢芯铝绞线(ACSR),该导线是由24股直径为2.78 mm的 LY9硬铝线和7股直径为1.8 mm 的A级强度镀锌钢绞线绞制而成;铝线分两层缠绕,外层15股、内层9股,中心为7股钢芯线(图1)。自制的导线微动装置(图2)的试验参数为:导线轴向静载荷为51 MPa,微动频率为10 Hz,偏心轮的偏心距分别为0.8 mm、1.0mm、1.2 mm和1.4 mm,循环振动周次依次为1.6×107、2.0×107和2.6×107。采用Zeiss EVO MA15型扫描电子显微镜(SEM)对Al股线疲劳断口及微动磨损区进行观测。同时,在微动Al股线的磨损区域取样,其截面经磨制、抛光后用10% NaOH水溶液腐蚀,在SEM下观察截面形貌。
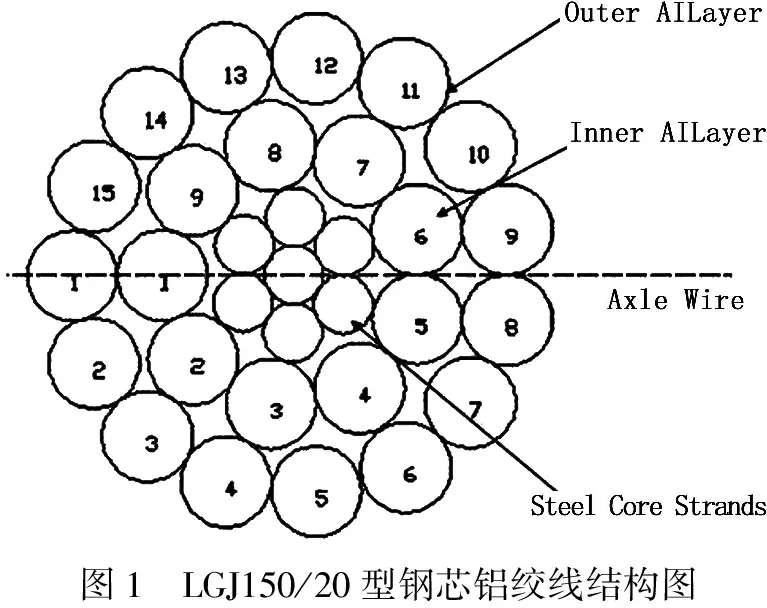
图1 LGJ150/20型钢芯铝绞线结构图
1.2 ACSR导线微动疲劳断裂状态
导线微动疲劳试验结果可知:仅微动振幅为1.0mm时导线发生线股断裂,且导线经历1.6×107循环次数时,出现一根断股。微动振幅为0.8 mm、1.2 mm和1.4 mm的试验中,未发现断股。
ACSR导线1.0 mm振幅微动1.6×107后,Al股线断股位置都位于导线与线夹最后接触点处。经历2.6×107周数微动,出现多根内外层Al股线的断裂。
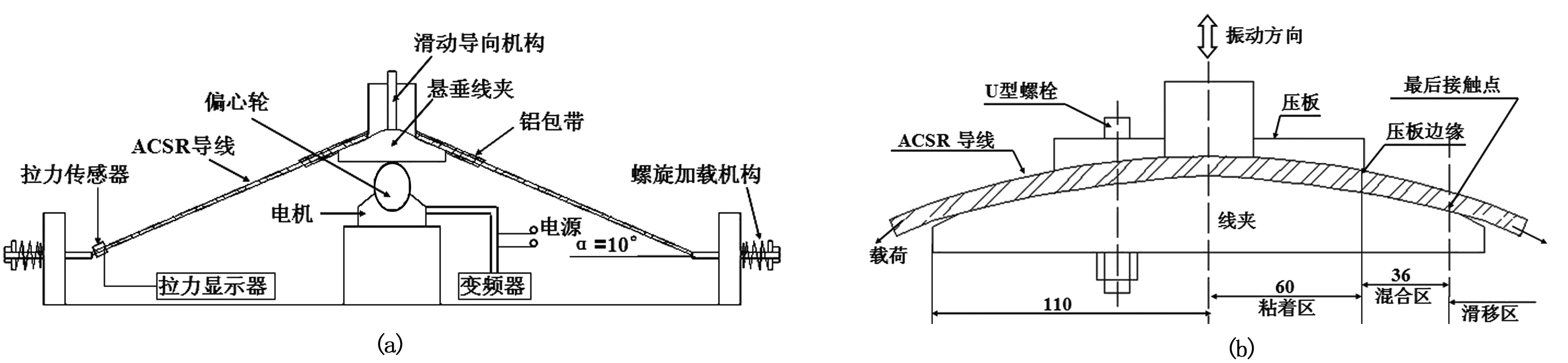
图2 导线微动装置及线夹系统
2 Al股线微动疲劳断口特征
内外层Al股线的断口分别呈现正断、45°断及“V”形断三种不同形态特征(图3)。但不论呈现何种断口形态,内外层Al股线都具有典型的微动疲劳断口,由疲劳源区、疲劳裂纹扩展区、瞬断区三个形貌不同的区域构成,如图2(a)。
2.1 疲劳源区
图2(a)中的A区为疲劳源区。疲劳源区是疲劳裂纹的萌生区。在ACSR导线微动试验中,微动混合区在最后接触点处是高应力区,导线由于微动磨损产生的表面损伤程度大,导致大的应力集中,在微动磨损表面分布大量径向裂纹,最容易发生Al线股疲劳断裂。
图3(a)所示为微动混合区磨损斑的磨损表面,依次为磨屑层、微动暗层及塑性变形层三个亚层。大量的裂纹从暗层萌生,一些微裂纹在暗层中交汇,促使材料脱离基体,形成磨屑;另有一些较大裂纹则穿过暗层和塑性变形层,深入到Al股线的基体中,形成扩展性裂纹,深入Al股线基体中的裂纹长度约为50 μm,据此可认为微动疲劳裂纹已萌生[2-3]。
在表面摩擦力(切向载荷)和外加载荷(正向载荷)共同作用下,Ⅰ型裂纹沿45°方向向深度扩展,扩展深度达到40 μm。因摩擦力随深度增加逐渐衰减,并在某一深度衰减为零,此后,在外加载荷单独作用下该裂纹偏转,促使Ⅱ型裂纹的形成[4]。
2.2 裂纹扩展区
在ACSR导线微动过程中,Al股线经历高周次的应力循环,疲劳裂纹经过反复的闭合与张开,缓慢地向导线内部扩展。裂纹扩展区(图3(a)中的B区)是Al股线断口上最重要的特征区域,占据了断口的大部分。该区域断口形貌的典型特征是贝纹线和疲劳辉纹。
贝纹线是疲劳断口的主要宏观特征。本文中ACSR导线的微动疲劳试验是由固定在电动机轴上的偏心轮转动带动悬垂线夹做上下往复运动来实现。当导线与线夹运动到最高点时,导线所受载荷最大;相反,当导线与线夹运动运动到最低点时,导线所受载荷最小(即为外加载荷),造成微动过程中ACSR导线中Al股线所受载荷发生周期性的变化,强度随微动振幅的增加而增大,导致在Al股线微动疲劳断口上出现贝纹线。
疲劳辉纹是疲劳断口的主要微观特征。Al股线微动疲劳断口上的疲劳辉纹是一系列弯曲呈波浪形并基本相互平行的条纹,其弯曲凸面指向裂纹扩展方向。

图3 Al股线断口SEM形貌像
2.3 瞬时破断区
瞬时破断区(图3(a)中C区)是微动疲劳试验中Al股线最后断裂的区域,是疲劳裂纹失稳扩展后形成的塑性断口,呈现大量的韧窝结构。在ACSR导线的微动疲劳试验中,随着疲劳裂纹不断扩展,当裂纹达到临界尺寸时,Al股线的有效截面减小,当外加应力超出Al股线的断裂强度时,疲劳裂纹发生失稳扩展,Al股线快速断裂。
3 ACSR导线微动磨损疲劳寿命预测
一般认为,构件微动寿命是由微动磨损寿命、 微动疲劳裂纹萌生寿命和微动疲劳裂纹扩展寿命三部分组成[4-5]。对Al股线,研究发现其微动磨损斑表面分布大量径向裂纹,这些径向裂纹在外加交变载荷下向线股内部扩展,如图3所示,最终导致线股疲劳断裂。据此可认为,线股微动磨损与疲劳裂纹萌生同时进行或是同一过程,因此,对Al股线进行断裂寿命估算时可只计算微动磨损寿命和疲劳裂纹扩展寿命。
3.1 ACSR导线微动疲劳寿命预测模型
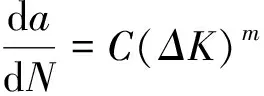
(1)
式中C、m为常数,与材料的微观组织结构、循环加载频率和波形、环境、温度及载荷比R相关;a0为构件中裂纹初始尺寸(一般认为,当裂纹尺寸达到材料晶粒尺寸数量级时,裂纹已萌生)[7],以构件中可观测到的最小裂纹尺寸计算,ac为构件断裂时裂纹的临界尺寸;ΔK为应力强度因子范围:
ΔK=Kmax-Kmin
(2)
式中Kmax、Kmin分别为一个疲劳应力循环中的应力强度因子的最大值和最小值:
(3)
式中Y是形状因子,大小取决于裂纹长度a与试样宽度W的比值,即Y=a/W;σmax、σmin分别为疲劳循环应力的最大值和最小值,Δσ为应力变程。
由以上各式可得:
(4)
对(4)式进行积分运算:
(5)
则有疲劳寿命:
(6)
3.2 ACSR导线微动疲劳寿命预测模型参数选择
(6)式中a0应选取疲劳源区裂纹纵深较小值,ac应选取疲劳裂纹扩展区长度较大值,这样就可以把导线表面微动磨损以及疲劳裂纹萌生所需的循环周次共同算入疲劳裂纹扩展所需循环周次,从而提高估算精度。
由以上分析,这里取a0=40 μm,ac=2 mm,对于Al股线,根据文献[8],C、m取值分别为:C=3×10-7,m=3.1。
由于疲劳裂纹萌生和扩展的驱动力是接触表面间的摩擦力,因此应力变程Δσ=2μPtanθ,其中μ为线股间摩擦系数,取μ=0.2[9];P为导线轴向应力,θ为导线与水平方向夹角,均为试验参数:P=51 MPa,θ=10°;考虑微动过程中导线的应力变化,应加上导线在偏心轮达到最高点时的微应变ε所对应的应力ΔP。其中:
b为偏心轮的偏心距,试验中分别用到0.8 mm、1.0 mm、1.2 mm和1.4 mm偏心轮的偏心距。
钢芯铝绞线的弹性模量:
式中,Eg、El分别是钢芯的弹性模量(136 500 MPa)和铝线股的弹性模量(59 000 MPa),Sg、Sl分别是钢芯的横截面积和(20 mm2)铝线股的横截面积(150 mm2),则微应变ε所对应的应力:
ΔP=E0ε
总的应力变程:
Δσ=2μ(P+ΔP)tanθ
3.3 ACSR导线微动疲劳寿命预测结果
分别计算不同振幅所对应的应力变程和疲劳寿命,如表1所示。

表1 导线微动疲劳寿命预测结果
振幅1.0 mm的微动导线,以1.6×107次为发生断裂的循环次数,则本研究所得模型预测寿命的估算误差为13.31%,通过计算得出的预测结果与实际试验结果相对误差低于20%,因此,可以认为本文选取的预测方法以及对参数的选择基本准确。
微动振幅为0.8 mm、1.2 mm和1.4 mm的试验中未发生断股,表明:随微动振幅增加,导线的疲劳寿命显著降低(表1),并在某一特定微动振幅(1.0 mm)达到最低点,其后随微动振幅增加,总的疲劳寿命回升。这是因为:一方面大的振幅使得材料的磨损加剧,疲劳裂纹交汇,形成磨屑,材料的疲劳反而降低[10];另一方面裂纹的萌生与扩展的驱动力是微动摩擦力和外加载荷,小振幅时,微动摩擦力与外载荷同相位,接触表面应力叠加会使裂纹扩展加剧;相反,大的振幅时,微动摩擦力与外载荷不同相位,二者相消,使得材料疲劳寿命增加[4]。与文献[7]所述材料的疲劳对于微动振幅存在阈值吻合。
4 结 论
(1)ACSR导线微动疲劳过程中,内外层Al股线的断股都发生在高应力区,即导线与线夹的最后接触点处,该处Al股线严重的微动磨损易促使疲劳裂纹萌生和扩展,最终导致Al股线断裂。
(2)导线断口呈现正断口、45°断口和“V”形断口三种形态,断口由疲劳源区、疲劳裂纹扩展区及瞬断区三个不同形貌特征区域构成。
(3)基于导线微动疲劳断裂机制,建立断裂力学寿命预测模型,预测结果与实际试验结果相对误差仅为13.31%,准确度较高,可以用以预测ACSR导线线股的微动疲劳试验寿命。
(4)断裂力学模型计算结果和实验结果显示:随微动振幅增加,导线疲劳寿命显著降低,并在一阈值振幅(1.0 mm)处达到最低;其后随微动振幅增加,导线疲劳寿命回升。
参考文献:
[1]Ouaki B, Goudreau S, Cardou A, et al.Fretting fatigue analysis of aluminium conductor wires near the suspension clamp: metallurgical and fracture mechanics analysis[J]. J Strain Analysis,2003,38:133-146
[2]周仲荣,Leo Vicent.微动磨损[M].北京:科学出版社,2002
[3]Fellows L J,Nowell D, Hills D A. Analysis of crack initiation and propagation in fretting fatigue: the effective initial flaw size methodology[J].Fatigue & Fracture of Engineering Materials & Structures, 1997, 20(1): 61-70
[4]何明鉴.机械构件的微动疲劳[M].北京:国防工业出版社,1994
[5]陶峰,欧阳祖行,刘正勋.微动疲劳寿命估算方法的研究[J].机械设计与制造工程, 2001,30(6):5-6
[6]Suresh S. Fatigue of Materials[M].Landon: Cambridge University Press,1991:193-197
[7]周仲荣.关于微动磨损与微动疲劳的研究[J].中国机械工程,2000(10):1146-1149
[8]Hubner P, Kiessling B, Biermann H, et al. Static and cyclic crack growth behavior of ultralfine-grained Al produced by different severe plastic deformation methods[J].Metallurgical and Materials Transactions, 2007,38(A): 1926-1933
[9]赵新泽,周权.LGJ150/25型钢芯铝绞线股线间接触有限元分析[J].制造业自动化,2011(6):122-125
[10]Guohong Chen,Xu Wang, Jiaqing Wang, et al.Damage investigation of the aged aluminum cable steel reinforced (ACSR) conductors in a high-voltage transmission line[J]. Engineering Failure Analysis,2012,19:13-21

