基于贝叶斯最小均方差的OCT图像散斑处理

, , ,

(上海师范大学 信息与机电工程学院,上海 200234)

光学相干层析技术(OCT)是近20年来发展快速的一种生物医学层析成像技术.由于OCT是基于相干光探测的成像技术,在图像中不可避免的会产生散斑.这种散斑噪声降低了图像的质量,掩盖了生物组织的结构细节,给医学诊断带来了很大的困难,所以对OCT图像散斑噪声处理有着很大的现实意义.

现在国内外对散斑处理的研究主要基于两个方面.一方面是改进OCT成像系统.OCT的成像质量与光源、数据采集速度、扫描速度、测量灵敏度等性能参数有关,Kim[1]等人提出了利用部分空间相干宽带光源来抑制散斑噪声.Pircher[2]等人提出了频域合成法,利用两个非相干信号来减少散斑,同时还保留了较高的空间分辨率.Desjardins[3]等人通过在多重散射角度上使用角度合成,能够降低散斑噪声等等.然而,以上这些方法都需要重新设计OCT系统,数据采集的时间也较长,并且在多数情况下散斑的抑制效果还受到一定程度的限制.

另一方面是研究OCT图像降噪算法.散斑抑制的算法仍然是OCT图像后处理的一个重要部分.通过对散斑噪声频谱分布、统计特性、图像特点的分析,提出了很多抑制OCT图像散斑的方法.Pizurica[4]等人提出了基于小波变换的方法,该方法减少了散斑噪声,但降低了微小结构细节的可见度;Puvanathasan和Bizheva[5]提出的Type II Fuzzy AD方法对低噪声的去除有好的效果,但对高噪声的滤除有一定的局限性.柯丽[6]等人提出了应用多级维纳滤波的方法对OCT图像去噪,该方法较好的抑制了散斑噪声,并且图像的视觉效果良好.苏鹏[7]等人提出了双树复小波和混合概率模型的方法抑制OCT图像的散斑,该方法抑制了散斑噪声并保持图像边缘锐度的相对稳定性.

1 OCT图像中的散斑

1.1 散斑的来源

散斑是由随机相位的散射光波干涉叠加产生的.在OCT成像系统中,光照射到存在大量的散射颗粒的样品组织内部发生散射,只有与参考光束光程差在相干长度范围内的散射光才能与参考光相干成像,然而在高散射生物组织中,相干长度内存在大量的散射颗粒截面,而被光电探测器接收的干涉光中既有单次背向散射光,又有多次散射光,光电探测器上会有光程差为nπλ的相干散射光束同时到达,产生高斯包络的具有相位差为nπ的交变电信号,它们彼此相干叠加就形成了散斑.不仅大量散射颗粒形成多次散射,在相干长度内不同深度截面上的散射光由于光程差引起的相位差也会形成散斑.另外生物组织还会吸收一部分光,使光的一部分频率丢失,这些频率的变化也会导致散斑的出现.所以,散斑的形成是非常复杂而且不可避免的[8-11].

1.2 散斑的数学模型

在OCT层析图像中,散斑依赖于成像光束的波长和成像对象的结构细节.因此,散斑携带了两个信息:成像对象的结构和噪声分量.由散斑噪声的统计特性可知,散斑噪声是一个乘性噪声[12],因此 OCT图像的信号模型可以表示为:

s(x,y)=f(x,y)·n(x,y) .

(1)

其中,(x,y)是OCT图像上的一个像素点二维坐标,s(x,y)是检测到的OCT图像信号数据,f(x,y)表示理想的无噪声信号数据,n(x,y)表示散斑噪声信号数据.

设M表示OCT图像的像素点的集合,m∈M表示OCT图像上的一个像素点的二维坐标(x,y),则表达式(1)可以表示成如下形式:

s(m)=f(m)·n(m) .

(2)

由于散斑噪声是一个乘性噪声,从散斑噪声中分离出无噪声信号的问题非常困难.可将检测到的OCT图像信号数据放在对数空间中,使得乘性散斑噪声变成一个加性噪声,从而利于散斑噪声的去除.将(2)式两边取对数:

log[s(m)]=log[f(m)]+log[n(m)] .

(3)

即：

S(m)=F(m)+N(m) .

(4)

其中,

S(m)=log[s(m)]，F(m)=log[f(m)]，N(m)=log[n(m)] .

2 算法的基本思想

2.1 贝叶斯估计

本文作者提出了一种基于非线性对数空间的贝叶斯最小均方差估计[13]的算法.该算法的关键思想是根据高斯噪声分布的特点,从噪声的高斯分布中抽取样本,对样本内的像素点赋予相应的权值,用加权直方图来估计后验分布p(F(m)|S(m)),从而计算出无噪声数据F(m)的贝叶斯估计值.

(5)

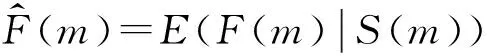
∑p(F(m)|S(m))F(m) .

(6)

表达式(6)显示理想的无噪声信号F(m)的最优贝叶斯估计,是以检测到的OCT图像信号的数据S(m)为条件的统计平均值.

2.2 图像像素的权值

如果把图像信号S看成是一个随机变量,那么加性噪声服从高斯分布.在对乘性散斑噪声取对数之后,散斑噪声转变成了加性高斯噪声分布.设m′是M中的一个随机点,m是图像邻域的中心像素点,以像素点m为中心的高斯分布表示如下:

(7)

其中,‖m′-m‖表示像素点m′到中心像素点m的平方欧氏距离,σspatial是高斯分布的空间尺度因子,确定图像邻域的尺度大小.设置σspatial为7个像素,即图像邻域的模板大小为7×7.从高斯分布Q(m′|m)产生的点m′是以m点为中心的邻域内的点.根据高斯分布的特点,m′满足的抽样条件是:

|u(m)-u(m′)|<2σ.

(8)

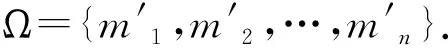
一幅图像邻域内的相邻像素之间是高度相关的,某一点的灰度值与其周围点的灰度值非常接近,在一幅图像中,如果一个像素点的灰度值远大于或小于其邻域的灰度值,则表明该像素点与其邻域像素点的相关性小,该像素点很可能为噪声点.像素之间的相关程度可用高斯分布的似然函数来描述:

(9)

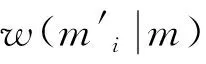
2.3 加权直方图

因为后验分布模型未知,所以这里采用直方图估计后验分布.直方图是对图像或图像的某个区域中每个灰度级分布情况的统计.但是直方图只提供了图像的灰度分布信息,而图像中的有效信号数据和噪声数据的分布情况却不知.为了区分图像中的有效信号和噪声,将图像像素的权值引入到直方图中,即加权直方图.

加权直方图[14-15]的思想是:在计算直方图时,给每个像素点赋予一定的权值,统计落入每一个直方图区间像素的加权个数.利用加权直方图来计算后验分布p(F(m)|S(m)),p(F(m)|S(m))表示以检测到的OCT图像信号的数据S(m)为条件的无噪声数据F(m)的概率分布.

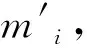
(10)

其中,δ是 Delta函数,z是归一化常数.根据归一化条件:

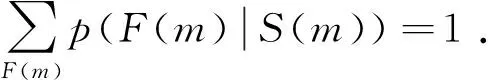
可得:

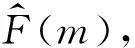
图1 算法流程图

3 实验结果

为了验证本算法的有效性和优越性,本文作者使用OCT实时成像图片进行处理,分别运用小波去噪,中值滤波去噪和本算法进行降噪处理.通过实验数据比较,来展现本算法的优越性.除了图片的视觉对比外,作者选择了2个定量的图像质量指标作为客观评价依据,一个是信噪比,另一个是等效视数.信噪比是用于比较被评价图像与原图像质量的参数,信噪比的数值越大,图像中的散斑噪声越少,图像质量越好.等效视数越大,表示图像上的相干斑越弱,散斑对图像的影响越小.信噪比[5](SAR)和等效视数[16](ENL)被定义如下:

SNR=10log10[max(S2)/σ2] .

(11)

(12)

其中,S代表图像像素的灰度值,σ代表图像像素的灰度值的标准差,u代表图像像素灰度值的平均值.

选取2张膀胱OCT实时成像图片,第一张图片的实验结果对比图像如图2所示.其中,(a)为原始图像,(b)为小波变换去噪后的结果图,(c)为中值滤波去噪后的结果图,(d)为本算法去噪后的结果图,表1为其客观对比数据.

第二张图片的实验结果对比图像如图3所示.其中,(1)为原始图像,(2)为小波变换去噪后的结果图,(3)为中值滤波去噪后的结果图,(4)为本算法去噪后的结果图,表2为其客观对比数据.

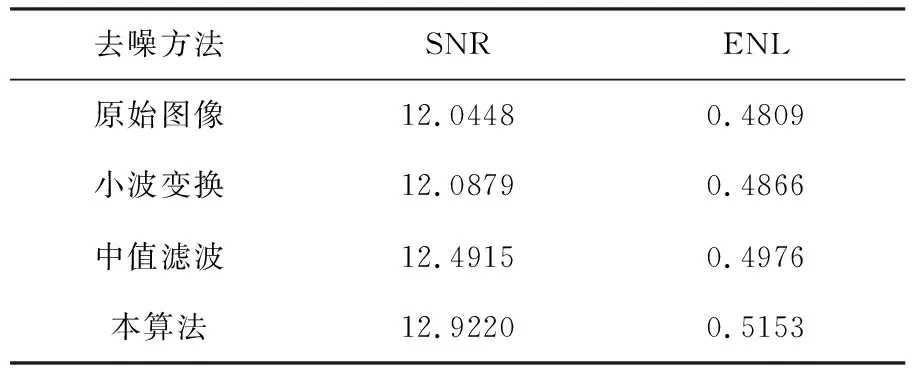
表1 OCT实时成像图片的客观数据

图2 第一张OCT实时成像图片处理结果

去噪方法SNRENL原始图像11.78630.4598小波变换11.85720.4702中值滤波12.32940.4762本算法12.54350.4767

图3 第二张OCT实时成像图片处理结果

4 结束语

为了抑制OCT图像的散斑噪声,通过对OCT图像散斑来源进行分析,并根据OCT的成像特点以及散斑噪声模型的分析,本文作者提出了一个基于对数空间的贝叶斯最小均方差估计的新算法.从表1和表2中的数据分析可知,与小波变换,中值滤波相比,算法在信噪比和等效视数方面都有明显的改善.这表明本算法去除OCT图像散斑后的图像质量更好,图像上的相干斑更弱,散斑对图像的影响更小.综上所述,本算法有助于降低OCT图像的散斑噪声,提高OCT图像的质量,在医学诊断中能够为医护人员提供清晰准确的图像信息.

参考文献:

[1] KIM J,MILLER D,KIM E,et al.Optical coherence tomography speckle reduction by a partially spatially coherent source[J].Journal of Biomedical Optics,2005,10(6):1-9.

[2] PIRCHER M,GTZINGER E,LEITGEB R,et al.Speckle reduction in optical coherence tomography by frequency compounding [J].Journal of Biomedical Optics,2003,8(3):565-569.

[3] DESJARDINS A E,VAKOC B J,OH W Y.Angle-resolved Optical Coherence Tomography with sequential angular selectivity for speckle reduction[J].Optics Express,2007,15(10):6200-6209 .

[4] PIZURICA A,PHILIPS W,LEMAHIEU I,et al.A versatile wavelet domain noisefiltration technique formedical imaging[J].IEEE Transactions on Medical Imaging,2003,22(3):323-331.

[5] PUVANATHASAN P,BIZHEVA K.Interval type-II fuzzy anisotropic diffusion algorithm for speckle noise reduction in optical coherence tomography images[J].Optics Express,2009,17(2):733-746.

[6] 柯丽,杜强,苏哲.应用多级维纳滤波的OCT图像除噪方法[J].光学精密工程,2008,16(4):740-745.

[7] 苏鹏,孙延奎,田小林.采用双树复小波和混合概率模型的光学相干层析图像去噪[J].应用科学学报,2011,29(5):467-472.

[8] MACIEJ S,IWONA G,DANIEL S.Efficient reduction of speckle noise in Optical Coherence Tomography[J].Optics Express,2012,20(2):1337-1359.

[9] SCHMITT J,XIANG S,YUNG K.Speckle in optical coherence tomography[J].Journal of Biomedical Optics,1999,4(1),95-105.

[10] 刘新文,王惠楠,钱志余.小波变换对OCT图像的降噪处理[J].光子学报,2006,35(6):935-939.

[11] 胡鹏.基于光学相干层析术的图像处理研究[D].南京:南京理工大学硕士学位论文,2010.

[12] 李自勤,王骐,李琦,等.激光成像雷达系统中散斑像的乘法模型及其滤除[J].中国激光,2003,30(8):717-720.

[13] WONG A,MISHRA A,BIZHEVA K,et al.General Bayesian estimation for speckle noise reduction in optical coherence tomography retinal imagery[J].Optics Express,2010,18(8):8338-8352.

[14] 王博.高噪声率红外图像直方图加权滤波算法[J].红外与毫米波学报,2007,26(5):380-385.

[15] 甘俊英,陈银河,高建虎.基于加权直方图和均值漂移的实时跟踪算法[J].计算机仿真,2008,25(11):208-211.

[16] 王晓军,孙洪.SAR图像相干斑滤波性能评估模型[J].雷达科学与技术,2008,6(1):33-34.