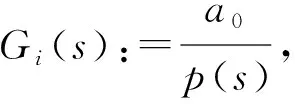一类控制模型的稳定性和单调性分析
,
(上海师范大学 数理学院,上海 200234)
0 简 介
基于反馈控制系统的设计可以解决3个问题:(1)渐近跟踪和干扰抑制类等信号,如阶跃、斜坡、正弦输入信号;(2)稳定性和鲁棒稳定性;(3)瞬时响应控制.其中前两个问题已经被很多人研究过[1-3].
对每一个控制系统来说,良好的瞬时响应是最重要的要求之一.在[4]中,提出了某一类所有极点都是负的互异实数的传递函数和其解析表达式,并证明了在封闭形式下,文章提出的分析公式,能被用来确定零点和最小的瞬时时间.在文[5]里提出的l1优化控制方法,明确地论述了在有界幅度输入下的时域响应问题,它也是少有的“现代”研究时间响应控制方法之一[6].基于渐近时间尺度和特征结构配置,对存在初始条件和外部约束的最小相位的多输入多输出系统,可以很好地解决跟踪问题,详细的方法见文[7].在文[8]和[9]中,主要讨论了欠控制阶跃响应和无最小相位零点的关系,而在文[10]和[11]中,提出了离散时间系统的无超调量控制.在[12]和[13]里,对传统控制方法作了很好的总结.
这里用一些新的结果来直接处理瞬时响应控制问题.其主要思想是根据特征多项式的系数和时域响应的关系.而这些关系是 Naslin 在1960年代初提出的,具体可见文[14].Manabe 在如何获得良好的动态响应控制系统的问题上,做出了重要的贡献[15].他利用系数图着重研究设备的一般行为,并已为许多工业系统成功地设计了控制器.而所谓的系数图则是以取对数标度来描绘设备系数和特征多项式的一种方法.这里,首先定义两个重要的参数集,分别被称为广义时间常数和特征比值.而这些参数呈现在多项式的系数里.这些依赖时域响应的参数,特别是响应速度和超调量,它们的特性是通过分析获得的.基于这些特性,本文作者设计了理想的传递函数和控制器,该控制器是最小相位的,同时其设计由相应程序给出.所得控制系统的瞬时响应满足独立指定超调量和上升时间.该控制器可能是状态反馈加前馈的控制器或双参数类型的控制器.同样的程序可用于非最小相位系统,也可能实现减少超调量和加快响应速度,尽管这些参数不能独立指定.Kim 等人已经较成功地利用了CRA[16]的方法,消除瞬时响应系统的超调量和加快系统响应速度.本研究在文献[16]基础上,来讨论双参数配置的控制问题,根据控制器结构 (图 1) 不妨考虑全极点传递函数G(s):
G(s)
(1)
在控制系统控制器设计时,由于现实情况,都会加入一些控制变量进去,以便进行更好地控制检测.如果(1)中p(s)是含有控制变量系数的多项式,系数ai(i=0,1,2,…,n)满足以下条件:
这里τ是一个常数.
本文作者将讨论使得多项式p(s)满足单调递增以及所有根的实部是非负的参数μ的条件,并进一步分析该系统的超调量和响应时间.
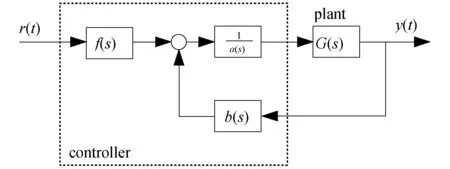
图1 双参数控制
1 单调性分析
先取
(2)
然后βk可以由γk表示,于是有:
βk=μγk,
(3)
(4)
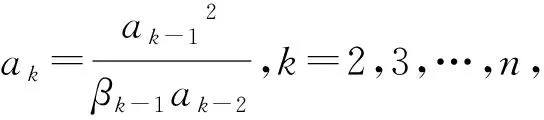
(5)
所以就得到:
(6)
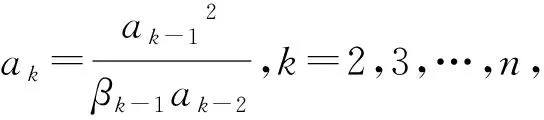
(7)
那么:
于是:
通过逐项累乘,于是就有:
由上很容易就得到以下公式:
(8)
其中a0=1.可以简化为:
(9)
可知:
(10)
事实上,有下面递推式:
(11)
那么,可以令:
(12)
引理1对于在 (12) 式中定义的Λk,有下面的 5 个结论:
(i)Λ1=Λn-1,Λ2=Λn-2,…
(13)
(iii) 随着n的增加,Λk逐渐减小.
(iv) 已知两个自然数n1和n2(n2 Λk(n1)≤Λk(n2) , (14) 等号当且仅当k=1时成立. (v) (15) 当n=2m-1 时, 当n=2m时,同理可得Λm-1=Λm+1. (ii) 按照 (i),能得到下面的结论: 所以Λk(n) 随着n增加而减少. (iv) 根据结论 (iii),当n1>n2时,对任意的k有: Λk(n1)>Λk(n2) , 等号当且仅当k=1时成立. (v) 定理1.1令p(s)=ansn+an-1sn-1+…+a1s+a0,这里ai满足式子(8),如果μ≥2,那么: (i) 频率幅度函数 |p(jw)| 是单调递增的; (ii)p(s) 的所有根的实部是非负的. 证明(i) 先考虑p(s) 的频率幅度函数 |p(jw)| 的平方,即: 根据式子(8),(11),可以定义: 那么: (16) (17) 那么G(ω)是单调递增的. 也就是,对μ≥2,i=1,2,…,n-1,每个ζk为正,所以得证. 其中: 于是定义: 对于所有w≥ 0 . (18) 式子(18)等价于: (19) 对于所有w≥ 0. 如果n是奇数(即n=2m+1),仿照(19)式,可以得到: (20) 这里k=1,2,…,n-2,要证明此式成立,需要借助下面 (21) 式. (21) 从(20)式,知道如果所有的ηi是正的,那么在(19)式中相位单调的条件满足.由引理1的结论(i),η1=ηn-2,η2=ηn-3,…, (22) 因此,可知ηi>0(i=1,2,…,m或m-1).从引理1的结论(ii),发现下面事实: 这里 (23) 在满足式子(21),(23)的条件下,很显然对任意i,如果有ηi(n1)是正的,那么ηi(n)也是正的,n>n1.当n→∞,k=1,2,…,n-2时, 于是当k≤m时: ∀μ>2 , 证明完成. 在定理1.1的基础上,进一步刻画μ的值. 定理1.2如果μ>1成立,p(s)(满足式(1))的幅度频率响应G(ω) 单调递增. 证明考虑 (10),(17) 式,如果有: (24) 基于以上结论,尝试运用数学软件Mathematica进行验证,数值结果显示有μ>μk,其中μk的部分值见表1. 定义Dμ(i,i+1)=|μi+1-μi|,i=3,4,…,n,…能够得到下面的事实: Dμ(i,i+1) 引理2考虑多项式f(s)=ansn+an-1sn-1+…+a1s+a0,如果多项式f(s)系数满足: (i) 当i=1,2,…,n-2且n≠5时,ai-1ai+2> 0.4655aiai+1; (ii) 当i=1,2,…,n-2且n=5时,ai-1ai+2> 0.4655aiai+1. 那么多项式f(s)是Hurwitz稳定的. 利用引理2,多项式p(s)是Hurwitz稳定的,只要以下条件成立: 引理3如果n≥2,那么: 证明定义: 则有: 显然: 因此A(i)在i=j时取到最大值. 定理2.1多项式p(s) 是 Hurwitz 稳定的,如果满足条件: 令: 容易计算,g(n)-g(n-1)≥0,所以当n→∞时,g取到最大值,即:g=1/0.4655=2.1482.因此μ≥1.46568.同时,通过数学软件的验证,也发现μ>μk,其中μk的值见表2. 类似的,定义Lμ(i,i+1)=|μi+1-μi|,i=3,4,…,n,…可得到: Lμ(i,i+1) Lμ(1000000,5000000)≐0 . 所以得到一个结论:只要μ≥ 1.46568,p(s) 满足 Hurwitz 稳定而且单调递增. 表1 μk的值 表2 μk的值 图2 不同的μ,不同的阶跃响应曲线 图3 μ=1.8,不同的τ值,不同阶跃响应曲线 参考文献: [1] DORATO P.Analytic feedback system design: interpolation approach[M].Pacific Grove,CA:Books Cole,2000. [2] ACKERMANN J.Robust Control: Systems with Uncertain Physical Parameters[M].New York:Springer-Verlag,1993. [3] BHATTACHARYYA S P,CHAPELLAT H,KEEL L H.Robust Control:The Parametric Approach[M].Upper Saddle River,NJ:Prentice-Hall,1995. [5] VIDYASAGAR M.Optimal rejection of persistent bounded disturbances[J].IEEE Trans Automat Contr,1986,31:527-534. [6] BOYD S P,BARRATT C.Linear control design:limits of performance[M].Upper Saddle River,NJ:Prentice-Hall,1991. [7] LIU K,CHEN B M,LIN Z.On the problem of robust and perfect tracking for linear systems with external disturbances[J].Int J Control,2001,74(2):158-174. [8] MITA T,YOSHIDA H.Undershooting phenomenon and its control in linear multivariable servomechanisms[J].IEEE Trans Automat Contr,1981,26:402-407. [9] LEóN DE LA BARRA B A.On undershoot in SISO systems[J].IEEE Trans Automat Contr,1994,39:578-581. [10] DEODHARE G,VIDYASAGAR M.Design of nonovershooting feedback control systems[J].Proc IEEE Conf Decision Control,1990,3:1827-1834. [11] ALEóN DE LA BARRA B,SALAZAR F J.Discrete-time systems with monotonic step responses and complex conjugate poles and zeros[J].IEEE Trans Automat Contr,2002,47:2098-2101. [12] CHEN C T.Analog and digital control system design:Transfer Function,State Space and Algebraic Methods[M].Ft Worth,TX:Saunders College Publishing,1993. [13] GOODWIN G C,GRAEBE S F,SALGADO M E.Control system design[M].Upper Saddle River,NJ: Prentice-Hall,2001. [14] NASLIN P.Essentials of optimal control[M].Cambridge,MA: Boston Technical Publishers,Inc,1969. [15] MANABE S.Coefficient diagram method,in Proc.14th IFAC Symp[C].Seoul,Korea:Automatic Control Aerospace,1998:199-210. [16] KIM Y C,KEEL L H,BHATTACHARYYA S P.Transient response control via charateristic ratio assignment[J].IEEE Trans Automat Contr,2003,48:2238-2244. [17] MIDDLETON R H,GRAEBE S F.Slow stable open-loop poles:Tocancel or not to cancel[J].Automatica,1999,35:877-886. [18] GOODWIN G C,WOODYATT A R,MIDDLETON R H,et al.Fundamental limitations due to-axis zeros in SISO systems[J].Automatica,1999,35:857-863. [19] JAYASURIYA S,SONG J W.On the synthesis of compensators for nonovershooting step response[C].Chicago:Proc Amer Control Conf,1992:683-684.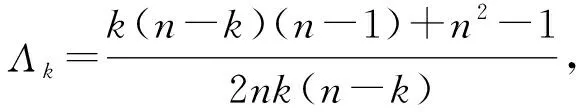
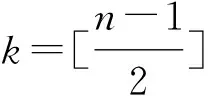
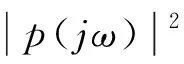
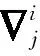


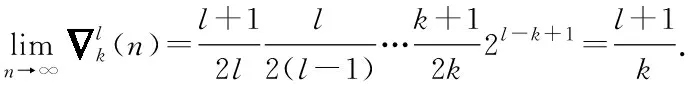
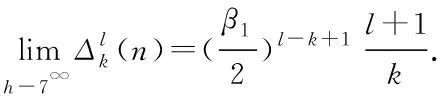
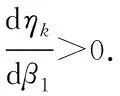
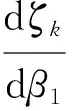
2 稳定性分析
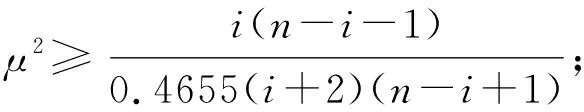
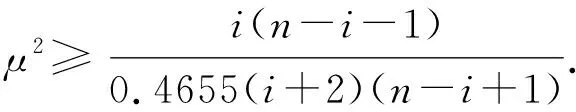
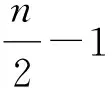

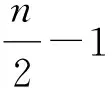


3 例 子