基于多系统的浅水区管节沉放对接精密定位方法
方长远,吕卫清,欧阳麟桦,赵建虎
(1.中交四航局第二工程有限公司,广东 广州 510231;2.中交第四航务工程局有限公司,广东 广州 510300;3.武汉大学测绘学院,湖北 武汉 430079)
沉管法隧道(以下简称为沉管隧道)拥有众多的优点,例如其对地基要求较低,特别适用于软基、河床或海床较浅、易于水上基槽开挖的工程地点;埋深小,包括连接段在内的隧道线路总长较矿山法和盾构法隧道显著缩短;沉管隧道端面形状可圆可方,选择灵活;基槽开挖、管段预制、浮运沉放和内部铺装等各工序可平行作业,彼此干扰较少,管段质量易于控制,施工周期短等[1]。管节沉放对接均在水下完成,其测量与陆地上传统方法具有很大的不同,管节对接精度要求高,施工定位难度大,对沉放对接的测控定位提出了更高要求[2~3]。长期以来,管节在沉放对接过程中多采用单一测量塔全站仪法,缺少有效的校验方法或措施[4~5]。特别是在沉管发生倾斜时,定位误差较大。为此,本文提出了一种基于多传感器组合的浅水区管节沉放和对接精确定位系统及数据处理方法。
1 系统组成及配置
整个测量系统由2台全站仪和3台GPS接收机组成。在管节前后控制点上各安装1座测量塔,在每个测量塔的塔顶面上安装流动站GPS天线、棱镜及姿态传感器MRU(Motion Reference Unit);在管节晒装时,借助自由设站法测定管节上控制点、对接点、MRU、GPS天线、棱镜中心在管节坐标系下的坐标。各设备的配置如图1所示。

图1 管节上设备组成及配置示意图
GPS测量采用RTK技术,基准站架设在岸边已知点上,流动站安装在测量塔上;全站仪测量采用自动跟踪技术,架设测量机器人同样设在岸边已知点上,基于极坐标法(即一点一方位法)对测量塔上的棱镜实施跟踪测量,确定棱镜的实时三维位置。
整个系统的观测数据通过网络发送到指挥中心接收机上,中心计算机根据原始观测数据实施数据处理,并进行管节状态信息的实时计算和显示。每个测量塔上配置两套电台,一台用于流动站GPSRTK三维坐标的发送,另一台用于姿态传感器MRU实时四维姿态参数的发送;在岸上,每台测量机器人上各配置一套电台,用于棱镜的实时三维定位坐标发送。监控中心配置一套电台,负责野外各发射单元观测数据的接收以及传输到计算机。
2 综合定位原理
2.1 管节坐标系的定义及各设备和控制点坐标的测定
为建立管节各控制点及设备之间的相互关系和确定其在工程坐标系中的坐标,需要建立管节坐标系[6]。管节坐标系的定义如下:将沉管控制点A定义为坐标原点;沉管中央纵向轴线定义为x轴,向前为正;过原点,与x轴正交定义为y轴,向左手为正;与xAy面正交,过原点A,垂直向上为z轴。A-xyz为右手坐标系。管节坐标系定义如图2所示。
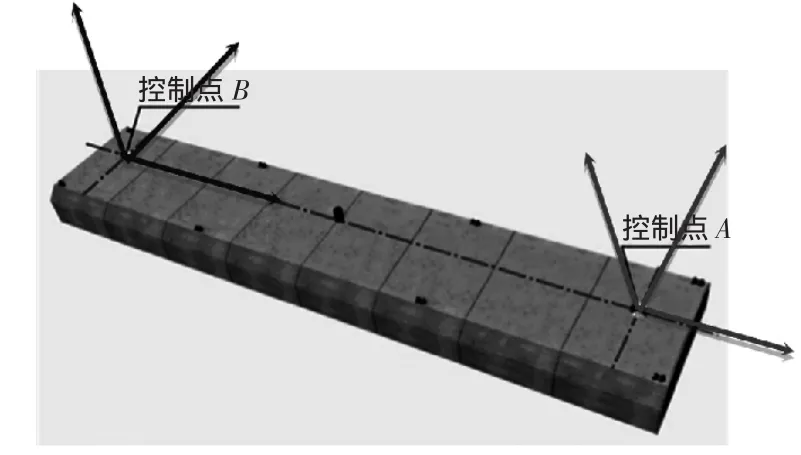
图2 管节坐标系的建立
考虑沉管的弹性变形,还应以沉管末端控制点B为原点,建立B-xyz右手管节坐标系,方便与后续管节下放和对接时的定位。为使沉管姿态监测与坐标轴定义一致,定义如下姿态角方向:Yaw:绕沉管Z轴,X轴向右旋转角度为正;Roll:绕沉管Z轴,沉管下旋为正;Pitch:绕沉管Y轴,上仰角为正。
采用自由设站法,对管节坐标系上各设备和控制点坐标进行测定,并将相对测站坐标系的各设备和管节控制点坐标转换到管节坐标系,分别获得A-xyz和B-xyz管节坐标系下设备和管节控制点坐标。
2.2 测量数据的质量控制及预处理
获得原始的边角观测数据后,需对这些观测数据进行质量控制。通过比较当前观测值与前一个观测值,对较差结果基于3σ原则进行异常判断。σ的取值需综合沉放速度及全站仪测量误差决定。
消除异常原始观测数据后,需对观测要素进行各项预处理,主要包括大气折射改正,距离和角度进行仪器偏差改正等处理,消除外部因素对观测要素的影响。在此基础上,对实测距离进行改算,并实现斜化平改正。

则棱镜的三维坐标(x,y,H) 为:

式中:S为观测斜距;D为转换得到的平距;θ为管节轴向方位角;δ为垂直角。(x0,y0,H0)为岸边控制点的三维坐标。
GPSRTK定位中,流动站接送机可以直接提供其天线相位中心的三维坐标。
由于两套系统实施独立定位,且均会形成一个时序,因此,可以借助Kalman滤波对异常定位解进行滤波处理。消除异常定位解,确保各控制点的精度和稳健性。

式中:Xk、Xk-1分别为k、k-1时刻状态矢量;Φk/k-1为状态转移矩阵;Wk-1、Γk-1分别为k-1时刻系统噪声和噪声系数矩阵;Lk、Ak和Vk分别为k时刻的观测矢量、观测矩阵和观测噪声。
2.3 归位计算
借助GPSRTK测量和全站仪测量,尽管获得了GPS天线相位中心和棱镜中心位置,但一方面由于不是对接位置,还需要转换才能获得对接点坐标,进而指导施工作业;另一方面,受管节沉放和对接时的姿态因素影响,简单的平移转换尚不能得到准确的对接点坐标。为此,需要结合实时姿态参数、各设备和控制点在管节坐标系中的坐标,结合姿态参数,通过归位计算,最终获得对接点的精确坐标。
以棱镜为对象,认为管节为刚体,理想管节坐标系下棱镜的坐标为(x0,y0,z0),受姿态因素影响,瞬时在理想坐标系下的坐标(x,y,z)为:

式中:p为纵滚角pitch;r为横滚角roll;R(p)为由纵滚角构成的3×3旋转矩阵;R(r)为由横滚角构成的3×3旋转矩阵。
类似的,对于对接点P,借助上式,可以计算瞬时P点在理想坐标系下的坐标(x,y,z)P。
获得了棱镜、对接点P在理想沉管坐标系下的管节坐标后,需结合管节的方位A信息以及棱镜在工程坐标系下的坐标,归位计算对节点在工程坐标系下的坐标。

式中:θ为沉管轴向方位角,可根据理想轴线方位角和航向角Yaw综合确定。

式中:R(θ)为沉管轴向方位角θ构成的旋转矩阵,为 3×3维。
类似的,基于测量塔上GPSRTK三维解,通过上述处理,也可以获得对接点在工程坐标系下的坐标(X,Y,Z)GPS-P。
2.4 测量成果的相互检验和融合
从归位计算过程可以看出,对于P点,存在源于棱镜、GPSRTK两个数据源的定位解,这为管节沉放和对接提供了多个参考源和检核条件。P点定位信息的可靠性可借助两套定位解较差结果的统计特性来判断。

而限差Δ则需要根据GPSRTK的定位精度和全站仪定位精度综合给出,若前者点位精度为±6.0 cm,后者为±1.0 cm,则Δ应为±6.1 cm。
当两套定位数据不一致时,需要分析出现异常的数据源。异常数据源可以根据前一个正确定位时刻定位数据结合管节运动速度综合判读。若两套定位数据一致,则最终的定位结果可借助加权平均来获得,即:
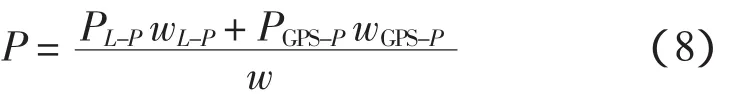
式中:w为总权重;wL-P和wGPS-P分别为棱镜归位计算所得位置的权重。考虑定位精度,实际定权中wL-P和wGPS-P分别定义为0.7和0.3。
3 数据处理流程
基于测量塔全站仪和GPS的管节沉放和对接精密定位过程如下:
1) 对原始观测数据,包括GPSRTK数据、全站仪观测数据、姿态传感器数据实施质量控制,消除异常观测的影响。
2)对原始观测数据进行预处理,基本观测元素如边长等实施各项改正,削弱环境因素对观测元素的影响。
3) 数据处理及测量设备位置三维坐标的计算。无论是全站仪观测还是GPSRTK测量,由于基准台站均架设在岸边已知点上,因此,可以根据观测元素,解算直接得到棱镜及GPS天线在工程坐标系下的坐标。
4)归位计算。获得了GPS和棱镜在工程坐标系下的坐标后,借助其在管节坐标系下的坐标、对接点(控制点)在管节坐标系下的坐标,以及姿态传感器提供的管节姿态变化参数,获得管节上包括对接点在内的各控制点的工程坐标系下坐标。
5) 对根据4),基于GPS和棱镜定位坐标所得对接点、各控制点的两套工程坐标进行数据一致性和可靠性检验,并基于式(8)进行融合,给出当前各控制点的最终坐标。
6)比较管节上各控制点的设计坐标和当前坐标,给出当前沉管的水平和垂直偏移量,进而指导实际管节沉放作业。
沉管对接参数计算及对接条件判断:
根据t时刻沉管中轴线上控制点A和B的坐标(XA,YA,HA)和(XB,YB,HB),可以计算沉管的方位A。
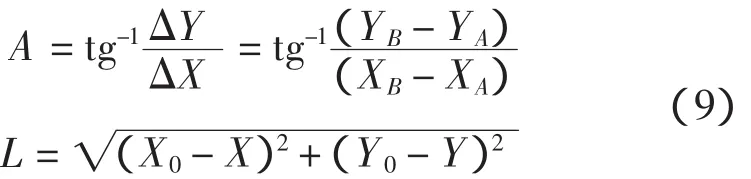
根据实时定位结果,满足如下条件时,认为待安沉管与已安沉管对接成功。
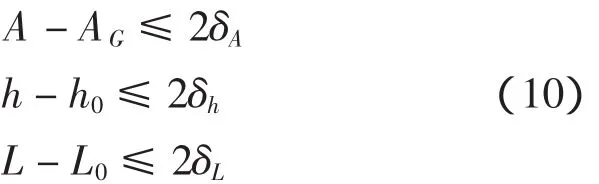
式中:A0为已安沉管管尾中轴线方位,或设计方位;h0为已安沉管表面对应控制点高程;L0为待安沉管与已安沉管对应控制点距离;A和AG分别为待安沉管管首(对接面) 和管尾方位;δA、δh和δL分别为测量误差引起的定向、高程和长度计算误差,根据式(10),若X、Y和Z方向定位精度分别为 σX、σY和 σZ,则有
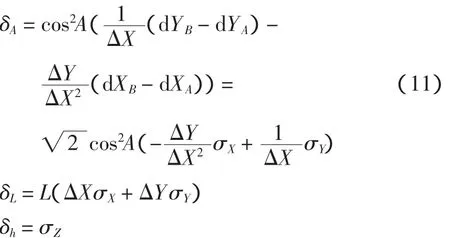
σX、σY和 σZ可利用式 (1) ~ (6),根据 X0、Y0、H0、A、p、r测量精度 mx0、my0、mz0、mA、mp和mr,借助全微分和误差传播定律获得。
4 实验验证及分析
为检验该综合定位系统及数据处理方法的正确性,开展了模拟实验,实验模拟管节沉放和对接过程(如图3所示)。试验中,主要采用了如下设备:待安沉管模型和已安沉管模型,尺寸均为3 m×2 m×1.5 m;GPS接收机2台套,一台作为基准站,另一台作为流动站安装在测量塔上;测量机器人1台,架设在已知点上,对沉管上的棱镜进行观察;棱镜2个,一个架设在已知点上,作为测量机器人跟踪的后视观测方向,另一个安装在模拟沉管上,作为测量机器人观测的前视方向。GPS罗经,由陀螺仪MRU和两个GPS天线组成,两个GPS天线分别安装在模拟管节顶面中轴线的前后端,MRU安装在模拟管节顶面中心位置。数据采集采用无线数据传输模块和电缆两种方式实现,其中,无线数据传输模块实现RTK、测量机器人定位数据向计算机的传输;GPS罗经数据通过通讯电缆实现数据传输;中心计算机实现数据采集、计算和图形显示。整个设备安装如图3所示。

图3 各设备在管节顶面的安装位置示意图
首先对图3所示各设备在管节坐标系下的坐标进行测定;然后利用吊车将待安沉管节吊至12 m高的位置,再缓慢下放;期间采集GPS罗经、GPSRTK和全站仪观测数据,根据以上数据处理流程,计算得到对接点坐标,并与设计坐标比较,基于式(9) 和式(10) 计算结果,指导沉放和确定对接时机。共开展了12次沉放对接试验,图4显示了其中第12次过程中各方向坐标的变化曲线。对12次沉放对接精度进行统计分析,测量塔全站仪定位和测量塔GPS定位精度统计结果如表1所示。

表1 整个试验中测量塔全站仪和GPS定位精度统计
从表1可以看出,全站仪定位精度要优于GPSRTK定位精度,这与实际情况一致,但均达到了厘米级定位精度。两个控制点Da和Db在12次综合定位中的精度如图5所示,从图中可以看出系统综合定位精度优于2 cm,从而表明本文所述方法的准确性。
为了进一步检验该系统的效果,在广州咀头洲沉管隧道工程开展了现场验证,从验证实验过程来看,本系统可以保证管节的顺利沉放、对接,对接精度:水平1 cm,垂直2 cm。

图4 第12组实验沉放对接过程中控制点Da、Db坐标变化曲线

图5 12次对接精度分布曲线
5 结语
综上所述,本文给出的基于姿态校对的测量塔全站仪和GPS管节沉放和对接定位系统及数据处理方法在理论上是正确的,实验表明,该系统在浅水区可以达到优于2 cm的定位精度,可以满足高精度管节沉放和对接的精度要求。
对于较长管节,不能认为整个管节在水下为刚体,而是一个弹性体,存在一定的变形,即邻近对接面的控制点坐标只能根据邻近测量塔上的GPS和棱镜坐标计算得到,而管节尾部控制点只能根据管节尾部测量塔上的GPS和棱镜位置归位计算得到。
本文提出的方法是针对浅水、近岸区域管节沉放的多系统对接精密定位方法,对于深水区,测量塔必须专门的设计,而且水中的测量塔会产生畸变误差,不能再将其视为刚体;对于远岸区,测量距离随之增加,将会给全站仪跟踪测量及成果的正确性带来显著影响。
[1]NESTORSRASMUSSEN.Concrete Immersed Tunnels-Forty Years of Experience[J].Tunnelling and Underground Space Technology,1997(12):33-46.
[2]常翔,张献伟.生物岛——大学城沉管隧道工程重难点浅析[C]//中国中铁隧道集团2007年水底隧道专题技术交流大会论文集.北京:中国铁道学会,2007:57-61.
[3] 李全海,何青.海底沉管隧道安放测量[J].海洋测绘,2004,24(6):34-36.
[4] 丁美,潘永仁.沉管隧道测量技术[J].现代隧道技术,2005,42(1):11-15.
[5] 杜云龙,刘千伟,王解先.常洪隧道管段浮运沉放测量及定位实时监控[C]//2003年上海国际隧道工程研讨会论文集.上海:中国土木工程学会,2003:433-442.
[6] 丁美.沉管隧道测量与实时定位技术[J].测绘通报,2009(S0):36.

