基于多重分形谱的道路交通事故分析
张晓红, 宇仁德, 张 强
(山东理工大学 交通与车辆工程学院, 山东 淄博 255091)
交通事故的发生受多种因素的影响,事故发生呈现出偶然性.看似没有规律可循的交通事故其实是受其内部的规律所支配的,这种规律已被证实,它是客观存在的.为了预防和控制交通事故的发生,使交通事故导致的损失降低到最小,国内外学者对道路交通事故的预测进行了广泛的研究.预测交通事故的方法很多,如灰色预测法、时间序列法、回归分析和BP神经网络等方法[1-2].多重分形理论的出现,为人们研究交通事故时间序列的内在规律提供了一条崭新的途径.
1 理论与方法
多重分形又称为多标度分形,是Mandelbrot在1972年研究湍流时首先提出的.多重分形是定义在分形结构上的由有限种或大量具有不同奇异标度指数的概率自己构成的非均匀分维分布的奇异集合.与常规的统计方法不同,多重分形的方法能将复杂体系分成许多奇异度不同的区域来研究,从而使我们能分层次地了解复杂体系内部精细结构和所富含的信息[3].通过对道路交通事故时间序列的多重分形分析能够找到多重分形谱参数与交通事故时间序列之间的关联性,并以一定概率预测交通事故的发展趋势.
多重分形谱的算法流程[4-5]如下:
(1)交通事故时间序列个数为N,令ε=n/N(n可被N整除),时间序列被分成1/ε个时间窗.
(2)令i=1,2,…,1/ε.设Si(ε)为第i个时间窗内时间序列的和,则Pi(ε)=Si(ε)/∑Si(ε),其中∑Si(ε)是全部时间序列的和.
(3) 选取适当的q值,通过Pi(ε)计算q的配分函数为
(1)
式中:q是-∞~+∞上的实数.
对于多重分形分布,配分函数随时间长度服从如下的标度关系:
Xq(ε)∝ετ(q)
(2)
(4) 根据式(2)作出相应的lnχq(ε)~lnε曲线,如果lnχq(ε)随lnε的变化有较好的线性关系,说明此分布属于多重分形分布.lnχq(ε)~lnε曲线的斜率就是τ(q),从τ(q)中可以计算出奇异指数α和多重分形谱f(α),其计算公式如下:
(3)
τ(q)=qα(q)-f(α)
(4)
分形谱的宽度Δα=αmax-αmin表征了最大、最小概率间的差别,也就是概率变化的不均匀性,表明多重分形的强弱变化程度.相应的最大、最小概率子集分形维数的差别Δf=f(αmin)-f(αmax)反映了事故出现频率的变化,Δf>0,曲线呈左钩状,表示在每组数据中事故达到最高点的次数多于达到最低点的次数;Δf<0,曲线呈右钩状,表示在每组数据中事故达到最高点的次数小于达到最低点的次数[6].
2 交通事故的多重分形分析
传统的时间序列预测,是利用预测目标的历史时间数据,通过统计分析研究其发展变化规律,建立数学模型,据此进行引申外推,预测其发展趋势的方法.
相比于传统的时间序列预测,多重分形对于时间序列的分析则表现出明显的不同.原因在于多重分形在处理时间序列时,是根据时间序列的易变性,将其分成许多奇异度不同的区域,通过具有时变性的参数(多重分形谱)来刻画时间序列的局部特征,真实地描述时间序列的统计特性,从而来获得时间序列内部结构的精细信息.
下面以2008年和2009年两年24个月的山东省道路交通事故次数为时间序列进行多重分形谱分析,交通事故次数如图1所示.
因为N=24,所以n取1,2,3,4,6,8,12,24这几个值,则ε的取值对应为 1/24,1/12,1/8,1/6,1/4,1/3,1/2,1.
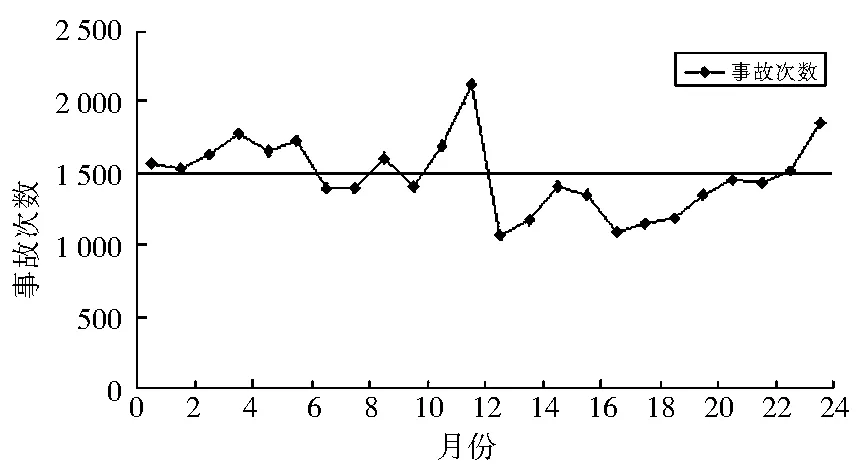
图1 交通事故次数
q取值为-50,-40,-30,-20,-10,0,10,20,30,40,50.利用matlab软件编程求出q的配分函数,并且画出lnχq(ε)~lnε曲线(如图2所示).

图2 lnχq(ε)~lnε曲线
根据matlab得出的结果如下:
(1)根据图2中lnχq(ε)曲线可知,lnχq(ε)随lnε的变化有较好的线性关系,说明该时间序列的分布属于多重分形分布,即交通事故时间序列具有易变性,具有统计分形的特征.
(2)根据lnχq(ε)~lnε曲线求出斜率τ(q),在spss中拟合q与τ(q)的函数关系,结果如图3所示.
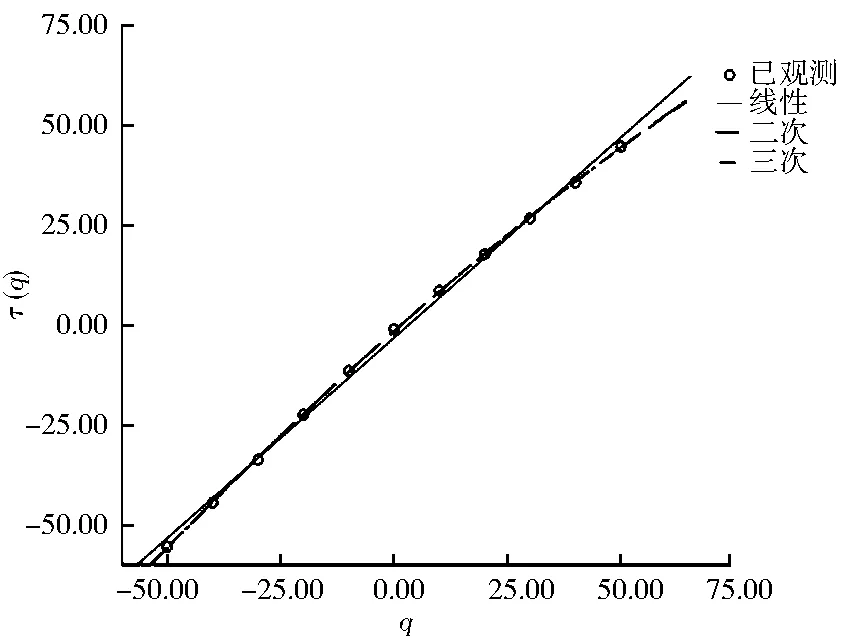
图3 q与τ(q)的函数关系图
(3)求出α(q)和f(α)的对应的取值(表1),作出多重分形谱f(α)-α(图4).

表1 f(α)和α(q)的值
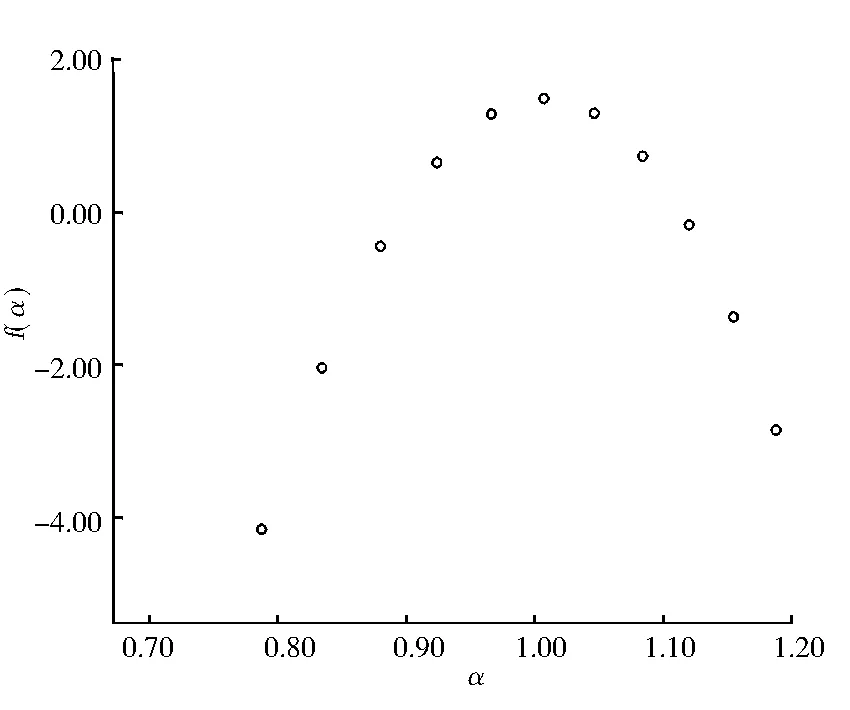
图4 f(α)-α谱
综上可得到如下结论:
最大、最小概率间的差别及分形谱的宽度为Δα=αmax-αmin=1.1875-0.7875=0.4,相应的最大、最小概率子集分形维数的差别Δf=f(αmin)-f(αmax)=-4.162+2.862=-1.3<0,表示在每组数据中事故达到最高点的次数小于达到最低点的次数,也就是说在未来年交通事故次数减少的概率大于事故次数增加的概率.
3 结束语
道路交通事故发生的规律尽管错综复杂,但仍然是可以预测的.传统的时间序列预测法无法充分描述交通事故时间序列的复杂行为,而多重分形谱为研究交通事故时间序列的局部特征提供了可能.本文通过求交通事故时间序列的多重分形谱,发现该序列属于多重分形分布,为交通事故研究提供了一种新的理论方法.在研究中,如何将多重分形理论与其他理论有机地结合起来,进而对道路交通事故进行有效的预测是未来努力的方向.
[1] 牛国宏.基于神经网络的道路交通事故预测[D].西安:长安大学,2006.
[2] 李相勇.道路交通事故预测方法研究[D].成都:西南交通大学,2004.
[3] 孙霞,吴自勤,黄畇.分形原理及其应用[M].合肥:中国科学技术大学出版社,2003.
[4] 孙洪泉.分形几何与分形插值[M].北京:科学出版社,2011.
[5] 杨小东,何爱军,周勇,等.复杂生理信号的多重分形质量指数谱分析[J].科学通报,2010,55(19):1 866-1 872.
[6] 程荣,毛军军,何其慧.金融资本市场的多重分形谱研究及实证分析[J].黄山学院学报,2009,11(3),37-43.

