二维各向异性位势薄体问题的虚边界元法

陈关忠， 周爱华， 张耀明

(山东理工大学 理学院， 山东 淄博 255091)

随着科学技术的进步与发展，各向异性材料由于在结构和性能方面具有众多的优越性而在工程中应用日趋广泛.特别是各向异性薄膜材料、薄体结构，如机械构件涂层、复合材料叠层构件、薄壳类构件、灵敏构件、以及纤维增强材料的粘结层等已广泛应用于工程中.但受其厚度尺寸的限制，结构物理量的数值分析一直是工程中的难点[1].采用有限元分析时，为了避免出现畸形单元，需按照薄体的厚度划分单元.可是，这样做必然会导致出现成千上万个单元，计算工作量剧增，对此小型计算机甚至无法完成.

边界元法能够有效地求解各向同性薄体结构问题[2-3]，但是奇异基本解的使用导致边界积分方程中不可避免地出现奇异边界积分和几乎奇异边界积分，这些积分的处理和计算具有相当的难度且耗时.各向异性薄体结构问题的边界元法是一个更困难的问题，至今取得的成果很少[4].

虚边界元法是一种无奇异边界元法，其最大优点是能够避免像边界元法求解边界物理量时遇到的奇异边界积分和求解近边界点处的物理量时遇到的几乎奇异边界积分.至今，虚边界元法已广泛应用于各种常规结构[5]及各向同性薄体结构[6-7]，但对于各向异性狭窄结构的研究尚未发现.本文拓展了虚边界法的应用范围，将其应用于二维位势各向异性狭窄结构，为各向异性薄体结构的研究开辟了新的途径，同时也拓展了虚边界法的应用领域.

虚边界元法的求解精度受虚实边界间的距离影响.本文选择近、中、远三种不同的虚、实边界间的距离，对不同厚度的各向异性薄体问题进行了计算，均获得了令人满意的数值结果. 表明虚、实边界间的距离选取非常地宽泛，且方法简单、效率高，即使结构的宽度狭窄到纳米级(10-9m)，依然可获得很高精度的数值解.

1 二维各向异性位势薄体问题的虚边界元法

本文假定Ω是R2中的一个有界区域，Γ=∂Ω是边界.n=(n1,n2)是区域Ω的边界Γ在x点处的单位外法向量.

1.1 二维各向异性位势薄体问题的控制方程

二维各向异性位势薄体问题的控制方程为

(1)

边界条件为

(2)

(3)

式中u为势函数，kij(i,j=1,2)为各向异性材料特性系数，n为边界外法向量，Γ1,Γ2分别是u和∂u/∂n已知的边界.

其通量为

(4)

二维各向异性位势薄体问题控制方程的基本解为

(5)

其中，x=(x1,x2),y=(y1,y2)分别为场点和源点，

令

则r(x,y)可表示为

r(x,y)=

1.2 二维各向异性位势薄体问题虚边界积分方程

设想假定Ω被嵌入一个无限的区域中，在Γ外的无限区域中有一延拓边界Γ′(这里称为虚边界)，沿着边界Γ′有一个待定的虚拟密度函数Φ(y)，令此虚拟密度函数对真实边界所产生的位势或法向梯度与边界条件一致，从而达到求解待定密度函数的目的.以上称之为虚边界元法.

各向异性位势薄体问题中的虚边界积分方程为

(6)

(7)

计算内点位势和位势梯度的边界积分方程表示为

(8)

(9)

2 虚边界积分方程的离散化方法

(10)

(11)

内点位势和位势梯度的离散公式可如法炮制，这里不再赘述.

不失一般性，假定边界为Dirichlet边界条件，则式(10)可以转化为如下矩阵形式

GΦ=F

(12)

这里G=[Gij]n×n，Φ=[Φ1,Φ2,…，Φn]T,F=[u(x1),u(x2),…，u(xn)]T,其中

由于此方法的积分点和场点分别位于虚边界和实边界上，因此无需考虑奇异积分，Gij可直接用标准高斯积分进行计算.本文算例均采用八点高斯积分公式计算.

由方程组(12)可求解密度函数Φ(y)，然后代入式(7)-(9)，进而依次求得边界的位势法向梯度、内点的位势和位势梯度.

3 数值算例

我们考虑一个各向异性薄体矩形和一个各向异性薄体圆环的数值算例，来验证本文方法的有效性，所有算例采用常单元等额配点法.为了表明方法数值解的准确性，定义平均相对误差如下：

(13)

虚边界元法的求解精度受虚实边界间的距离影响.以下算例中，我们选择近、中、远三种不同的虚实边界间的距离，对不同厚度的各向异性薄体问题进行了计算，都获得了令人满意的数值结果，表明虚实边界间的有效距离选取范围非常地宽泛.

算例1各向异性薄体矩形区域的热传导.如图1所示，薄体矩形区域的长度l=1m，厚度为h从10-1m到10-9m之间变化，各向异性材料的系数为k11=2,k12=1,k22=3，边界条件为在短边上已知通量q，在长边上已知温度u.本问题的精确解为u(x,y)=x2-y2+xy.

图1 各向异性薄体矩形区域的热传导

如图1所示，取虚边界与结构外表面的几何形状相似，将两短边各划分为2个单元，两长边各划分为10个单元，共划分为24个单元.在薄体矩形的两短边边界上各均匀地选取20个计算点；在两长边边界上各均匀选取40个计算点，虚、实边界间的距离d分别取1、20、40，计算不同厚度h的板在短边边界上40个点处的温度和长边边界上80个点处的通量.图2和图3描述了所得结果的平均相对误差.从中可看出，当板的厚度从10-1m到10-9m变化时，d=20和40时的数值结果具有很高的精度；d=1时，结果的精度稍差，但仍具有较高的精度.这表明虚、实边界间的距离选取相当地宽泛.

图2 边界点温度的平均相对误差

图3 边界点通量的平均相对误差

在薄体矩形区域内均匀地选取100个计算点，当h=10-9m和d=10时，计算这些点处的温度，图4给出了计算结果的误差曲面. 可看出，数值结果的相对误差非常地小.这表明该方法能够有效地求解厚度小到纳米级的各向异性薄体问题.

当h=10-9m和d=20时，随着边界单元数的增加，计算短边边界上40个点处的温度和长边边界上80个点处的通量，其数值结果的平均相对误差变化列于图5.计算时，长、短边划分单元数的比例为5∶1.可看出，随着单元数的增加，相对误差迅速地减小，说明该方法具有良好的收敛性.

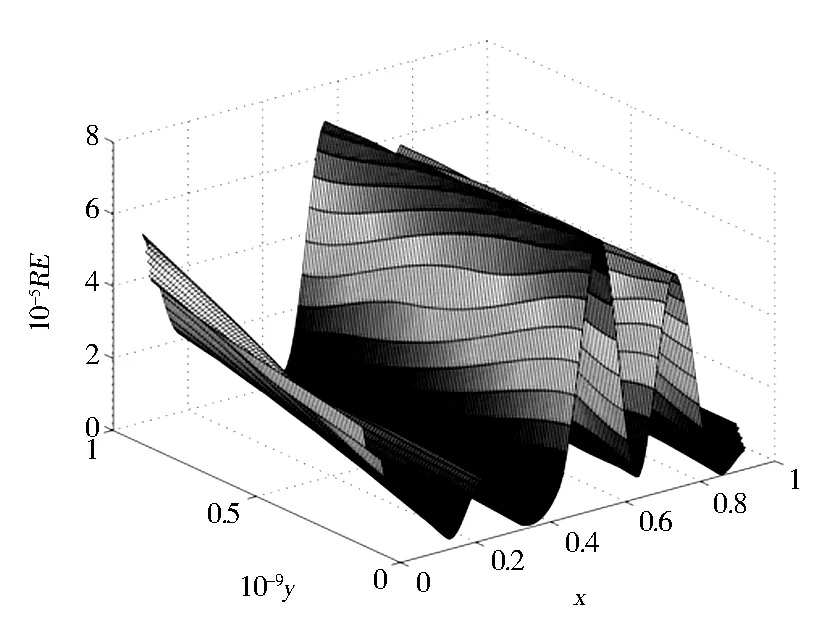
图4 内点温度的相对误差曲面

图5 边界点温度和通量的收敛曲线

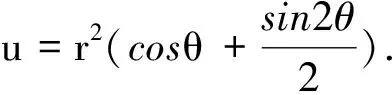
图6 各向异性薄体圆环区域的热传导

图7 外边界点温度的平均相对误差

图8 内边界点通量的平均相对误差

在薄体圆环区域内均匀地选取100个计算点，当h=10-9m和d1=0.6,d2=20时，计算这些点处的温度，图9给出了计算结果的相对误差曲面. 可看出，数值结果的相对误差非常地小.这表明该方法能够准确高效地求解厚度小到纳米级的各向异性薄体问题.

当h=10-9m和d1=0.6,d2=20时，随着边界单元数的增加，计算外边界上100个计算点处的温度和内边界上100个计算点处的通量，图10给出了数值结果的收敛曲线.计算时，内外边界划分单元数的比例为1∶1.可看出，随着单元数的增加，相对误差迅速地减小，说明方法仍然具有较好的收敛性.

图9 内点温度的相对误差曲面

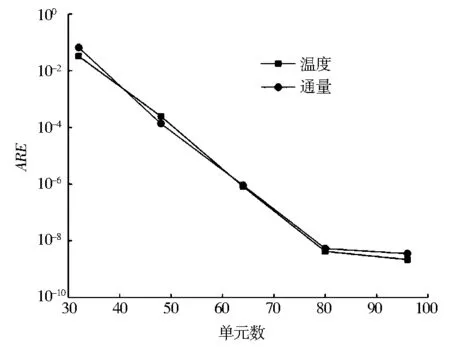
图10 边界点温度和通量的收敛曲线

4 结束语

本文提出求解二维各向异性位势薄体问题的虚边界元法，给出求解此类问题的新途径，同时拓展了虚边界元法的应用领域.数值算例表明，虚边界元法能够非常有效地求解二维各向异性位势薄体问题，而且虚、实边界距离的选取相当地宽泛，即使结构的厚度小到10-9m，依然可获得高精度的数值解.

[1] Luo J F,Liu Y J,Berger E J.Analysis of two-dimensional thin structures(from micro-to nano-scales) using the boundary element method[J].Computational Mechanics,1998,22:404-412.

[2] Zhang Y M, Gu Y, Chen J T.Analysis of 2D thin walled structures in BEM with high-order geometry elements using exact integration[J]. Computer Modeling in Engineering and Sciences, 2009, 50(1):1-20.

[3] 张耀明，刘召颜，李功胜，等.各项异性位势平面问题的规则化边界元法[J].力学学报, 2011，43(4):785-788.

[4] Zhou H L, Niu Z R, Cheng C Z，etal. Analytical integral algorithm applied to boundary layer effect and thin body effect in BEM for anisotropic potential problems[J]. Computers and Structures,2008,86:1656-1671.

[5] 孙焕纯，张立洲，许强，等.无奇异边界元法[M].大连：大连理工大学出版社，1999.

[6]袁飞，屈文镇，张耀明.二维薄体结构位势问题的虚边界元法[J].山东理工大学学报:自然科学版，2012,26(3)：18-21.

[7]屈文镇，袁飞，张耀明.二维弹性薄体问题的虚边界元法[J].山东理工大学学报：自然科学版，2012,26(3):64-67.