常用系统发育树构建算法和软件鸟瞰

张丽娜，荣昌鹤，何 远，关 琼，何 彬，朱兴文，刘佳妮，陈红菊3,,*

1. 大理学院 数学与计算机学院，云南 大理 671003

2. 云南林业职业技术学院，云南 昆明 650224

3. 红河学院，云南 蒙自 661100

4. 中国科学院昆明动物研究所 遗传资源与进化国家重点实验室，计算生物学与医学生态学研究组，云南 昆明 650223

系统发育就是指生物谱系的分支演化历史，或是指生命自起源后的整个遗传进化史 （Avise，2006），系统发育树是描述物种间或操作分类单元间（operation taxonomic units，OTUs）系统发育关系的图论模型。操作分类单元可以是现存物种、基因、基因组或者是任何其他可操作单元。系统发育树的构建就是从现存物种和古生物学记录存留的证据来重现生命进化史的科学探索。用伟大的进化生物学家 Dobzhansky（1973）的名言“如果没有进化论，生物学的一切便毫无意义”来强调系统发育树的重要性是恰如其分的。

由于技术限制，最初分类学家只能依靠生物的形态特征来推断物种间的亲缘关系。但表型特征存在一定的局限性，由于趋同进化现象，有时候亲缘关系很远的生物体也表现出很大的相似性，如鲸和蝙蝠，虽然形态差异很大，但都具有发达的高频回声定位能力。同时，许多生物个体可能由于体型较小，数量多而导致对其表型特征的研究较困难，如各类微生物。另外许多生物体间的共同特征少之又少，很难发现何种表型特征能用来研究比较。随着分子生物学研究的不断发展和检测核苷酸序列和各种氨基酸序列技术的成熟，使得从小分子层面上构建系统发育树成为可能。近年来测序技术的迅猛发展，使得测序成本降低，涌现的海量核酸序列、氨基酸序列数据也被收集于如 GenBank、EMBL和DDBJ 等大型数据库中，促使人们可从更大范围上建立物种间的遗传进化关系。分子水平的进化研究具有传统方法不可比拟的优势，可从核酸和氨基酸序列差异程度来精确判断物种进化的时期和速度，确定亲缘关系极远的生物体间的进化关系，同时能对体型较小的微生物间的进化关系进行深入研究。

目前许多系统发育树构建算法都是从解决最优化问题出发，如最大简约法、最大似然法等，但是这些方法受物种数量严格限制，当物种数量较多时，构建系统发育树是一个典型的 NP-complete 难题 （Foulds & Graham，1982）。这意味着在多项式时间内不能被计算机求解，只能被非确定机求解；不能得到绝对数值解，只能通过比较相对解来确定最合适的答案。然而庆幸的是人们后来发明了改进算法：启发式搜索算法，通过分割数据集 （操作单元）变成小的子集，再对小的子集使用最优化算法 （最大似然或最大简约算法等）求出每个子集对应的最优树，然后合并每个子集得到的最优树，最终形成整个数据集的最优树。

随着生物信息学的发展，使用计算机技术处理系统发育树成为不可或缺的理论，构建系统发育树的软件包的相继出现，并得到了广泛的应用。对构建进化树程序包的算法、运用限制条件及其优缺点的了解，有助于我们选用合适的建树方法和分析软件，更进一步说，为我们对现有方法的改进和编写性能更完善的软件提供思想源泉和帮助。

1 构建系统发育树的一般过程

不同的领域对树有不同的定义，下面简单列举了部分树的定义及生物信息中与系统发育树相关的基本术语。

树（图论中定义）：连通的无环图称为树。度为 1 的叫叶子节点，度大于等于 1 的为根节点，节点间的连线叫树枝。

树（数据结构中定义）：由一个集合以及在该集合上定义的一种非线性结构关系。

树（生物信息中定义）：表示物种之间的进化关系的树状图谱。由树枝和节点组成。节点分为内部节点和外部节点，内部节点代表的是进化事件发生的位置或进化过程中的共同祖先，外部节点又叫叶子节点，代表的是不同物种或是可操作单元。树枝是连接各节点的边，树枝长度代表的是生物进化时间或进化距离。叶子节点的度为 1，内部节点的度至少为 3。如图 1a 所示，节点 A−D 为叶子节点，节点 1、2 为内部节点，节点 0 为根节点。根据拓扑结构的不同系统发育树可以分为有根树和无根树。有根树（图 1a）有一个根节点，代表所有其他节点的共同祖先，从根节点只有唯一路径经进化到达其他任何节点；无根树（图 1b）只表明了节点之间的关系，没有进化方向，但是通过引入外群或外部参考物种可以在无根树中指派根节点（Gregory，2008）。

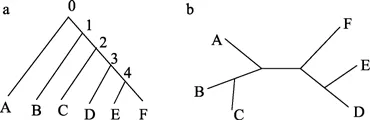
图1 系统发育树Figure 1 Phylogenetic treea：有根树；b：无根树。 a: Rooted tree; b: Unrooted tree.

构建系统发育树包括选择同源序列、序列比对、计算推断进化树、评估进化树四个步骤。具体流程如图 2 所示。

图2 构建系统发育树流程图Figure 2 Phylogenetic tree flowchart

构建系统发育树的第一步是选择同源序列作为计算数据。这一步实际上包含两个过程：一是收集序列数据，二是确定数据的同源性。序列数据可以通过实验或通过公共数据库下载获得。目前公共数据库主要有美国的 GenBank、欧洲的 EMBL、日本的 DDBJ 等。

序列比对提供一种衡量核酸或蛋白质序列之间相关性的度量方法。将两条或多条序列写成两行或多行，使尽可能多的相同字符出现在同一列中，将不同序列中的每一位点进行逐一比对，构建一个打分矩阵来表示序列间的相似性或同源性。DNA序列在进化中由于替换、插入/删除、突变事件使其发生改变，所以在比对中，错配与突变相应，而空位与插入或缺失对应。最常用的比对工具有Blast（Altschul et al，1990）、Clustal（Larkin et al，2007）、 Muscle（Edgar，2004）和FASTA（Lipman & Pearson，1985）等。

计算推断系统发育树的主要任务是求出最优树的拓扑结构和估计分支长度。这部分算法及常用软件在后面详细介绍。

评估的目的是对已经得出的系统发育树的置信度进行评估，常用的方法有自举检验法 （bootstrap methods）（Felsenstein，1985；Penny & Hendy，1985）及刀切法 （jackknife methods）（Shao & Tu，1996）。自举检验法是从原始序列中随机选取碱基组成和原始序列相同长度的新序列，这样在每个序列中有些碱基被重复选择，而有些碱基未被选择，按这样的方法取出和原始数据序列数相同的新序列组成新的组。将所有的新序列组用某种算法生成多个新的进化树。将生成的许多进化树进行比较，把所有新的树中相同拓扑结构最多的树认为是最真实的树，树中分支位置的数值表示该种结构占所有树中的百分比值，该值小于 75通常都认为是置信度较低的分支。刀切法是对原始数据进行“不放回式”随机抽取，从数据集里去除一部分序列数据或每次去掉一个分类群对象，然后对剩下的数据进行系统发育分析。刀切法产生的数据小于原始数据，（delete-half-jackknifing）（Felsenstein，1985；Wu，1986）。两类检测方法的差别在于，前者是对全部数据进行“重置式”随机抽取，数据抽到的概率是相等的，且建立的和原始数据大小相等，而后者是“不放回式”抽取，产生的数据小于原始数据。

2 构建系统发育树常用算法原理

基于分子水平的系统发育推断方法可以分为两大类，即基于离散特征的方法和基于距离的方法。基于离散特征的系统发育树重构算法通过搜索各种可能的树，从中选出最能够解释物种之间进化关系的系统发育关系树，这类方法利用统计技术定义一个最优化标准，对树的优劣进行评价，包括最大简约法（maximum parsimony methods）（Mount，2008）、最大似然法 （maximum likelihood methods）（Myung，2003）和贝叶斯法（Bayesian methods）（Holder & Lewis，2003）。距离法的理论基础是最小进化原理（minimum evolution，ME）（Saitou & Nei，1986），这类方法首先构造一个距离矩阵来表示每两个物种之间的进化距离，然后基于这个距离矩阵，采用聚类算法对研究的物种进行分类。通过不断的合并距离最小的两个节点和构建新的距离矩阵，最终得出进化树。距离法包括非加权组平均（unweighted pair-group method with arithmetic mean，UPGMA）、邻接法 （neighbor- joining，NJ）、距离变换法（transformed distance method）和邻接关系法（neighbors relation method）等（Takezaki，1998）。非加权组平均法比较简单，得出的系统发育树不可加和，现在很少使用，常用邻接法来构建系统发育树。表1列出了常用构建系统发育树的算法及支持软件。

2.1 邻接法

Kidd & Sgaramelh-Zonta（1971）最早提出基于距离数据的系统发育树重构算法，从所有可能的进化树中选择进化分支长度总和最小的那棵树，距离法通常不能找到精确的最小进化树，只能找到近似的最小进化树，但是它的计算速度非常快，而且准确率较高，因此被广泛应用于系统发育分析（Zhang & Lai，2010）。当可操作单元数量较多时，这种方法的计算量会大增，因此，又提出了启发式搜索算法（Mucherino & Seref，2009）：从一个距离矩阵开始，采用一定的准则，递归地合并矩阵中距离最短的节点，并重构新的距离矩阵，直到只剩下最后一个分类单元为止。其中最常用的是邻接法（Saitou & Nei，1986）。下面举例说明邻接法重建系统发育树的过程。假设有以下 5 组同源序列：

S1: GTGCTGCACGGCTCAGTATAGCATTTA CCCTTCCATCTTCAGATCCTGAA

S2: ACGCTGCACGGCTCAGTGCGGTGCTTA CCCTCCCATCTTCAGATCCTGAA

S3: GTGCTGCACGGCTCGGCGCAGCATTTAC CCTCCCATCTTCAGATCCTATC

S4: GTATCACACGACTCAGCGCAGCATTTGC CCTCCCGTCTTCAGATCCTAAA

S5: GTATCACATAGCTCAGCGCAGCATTTG CCCTCCCGTCTTCAGATCTAAAA

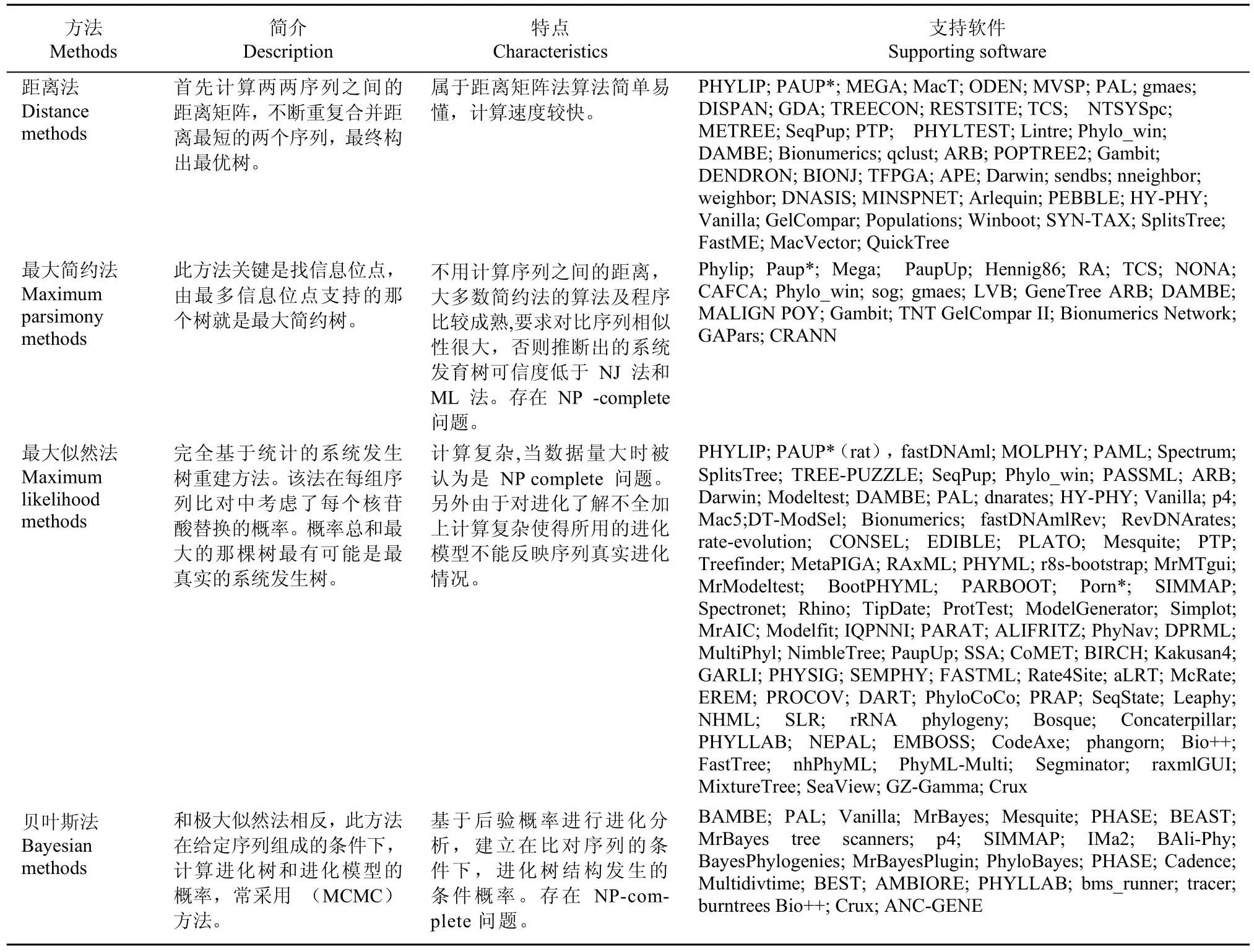
表1 系统发育树常用算法及支持软件Table 1 Frequently-used algorithms and software for phylogeny reconstruction(http://evolution.genetics.washington.edu/ phylip/software.html)

以上5个序列中每个序列都含有50个碱基，每两个序列之间的距离定义为失配碱基的个数（这里忽略删除和插入事件）。则每次聚类可得出距离矩阵如表 2、3、4 所示。根据公式1

求出Q值。公式中 n 为物种个数或序列个数，在 n个序列组成的所有可能的无根树中找出 Q 值最小的两个序列组成邻近关系，重新构建距离矩阵，根据新的距离矩阵再找最小的 Q 值组成一组，反复上面的过程直到所有的序列都找到了自己的邻居（Studier & Keppler，1988）。根据表2、3、4求出所有的 Q 值，见表5。

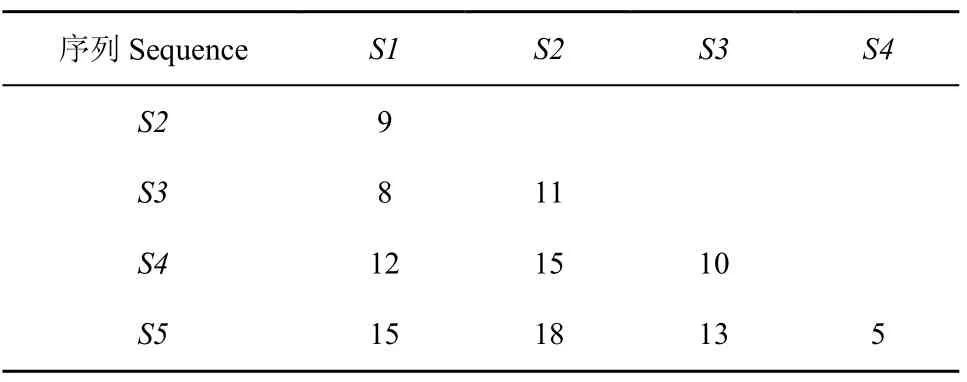
表 2 序列间距离矩阵Table 2 Pairwise distance matrix

由表 5 可推断出 5 条序列的系统发育树拓扑图和各分支长度分别如图3和图4所示：

表3 第一次聚类得到的距离矩阵Table 3 Distance matrix after the first clustering

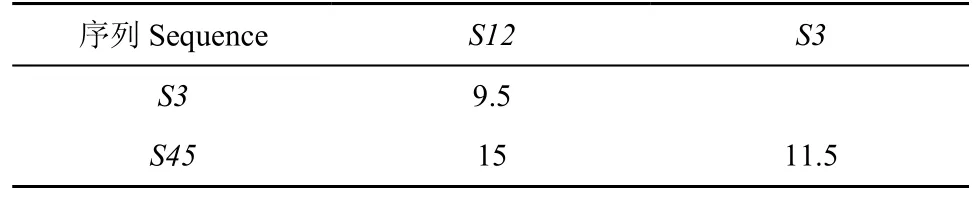
表 4 第二次聚类得到的距离矩阵Table 4 Distance matrix after the second clusterin

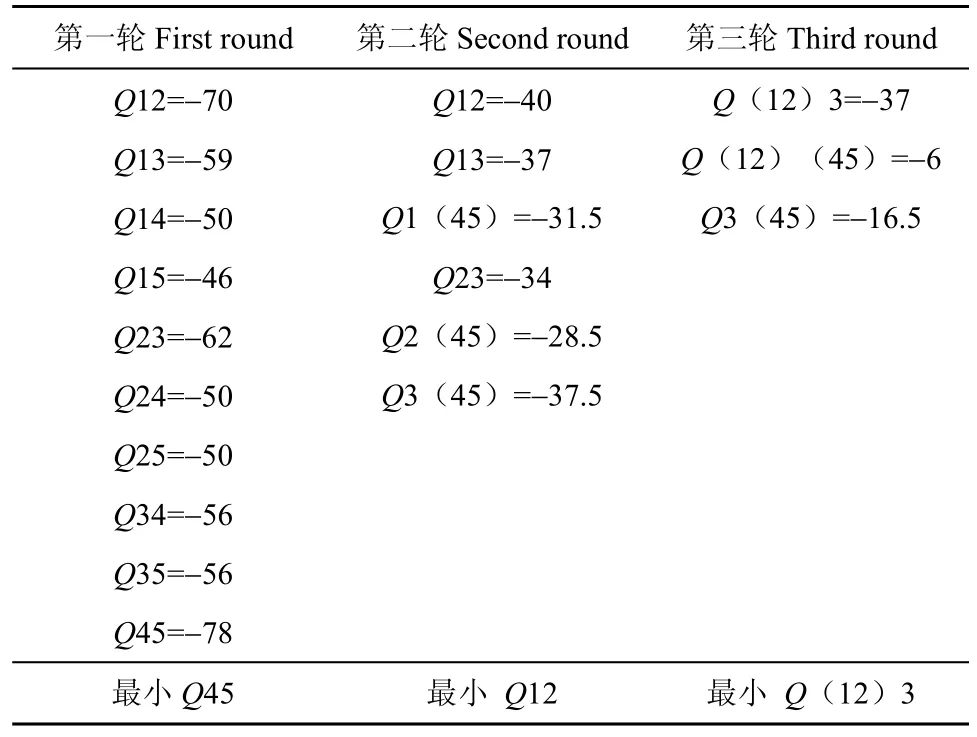
表 5 Studier J 和 Keppler K 方法得到的 Q 值表Table 5 Q value from Studier J and Keppler K

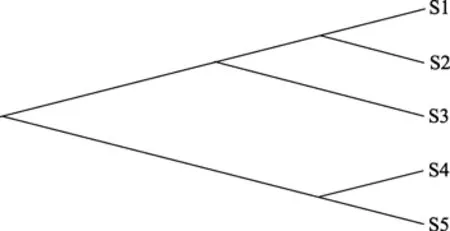
图 3 NJ算法得到的系统发育树拓扑图Figure 3 Topology of Phylogenetic Tree with NJ Approach

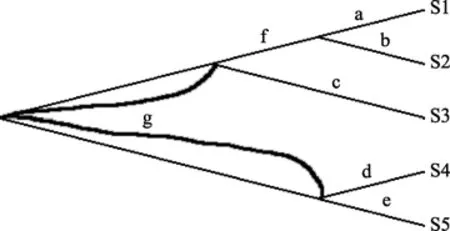
图4 估计各分支长度Figure 4 Branch-Length Estimation

随后的研究在邻接法基础上又提出了很多改进算法：Studier & Keppler（1988）提出的改进算法，引入了线性数组的概念，大幅降低了计算的时间复杂度（Chen et al，2006）；Bruno et al（2000）提出了加权邻接法（weighted neighbor-joining）算法、Gascuel（1997）提出了 BIONJ 算法、Desper &Gascuel（2012）提出的 FASTME 算法和Criscuolo& Gascuel（2008）提出了快速邻接法算法，均缩短了建立系统发育树的时间。距离法速度快，适合于大型数据集和自举分析,允许不同序列间有不同的分支长度,允许多重替换，但当序列差异很大时，转换成距离矩阵会使序列信息减少，而且距离法只提供一棵可能的树，并对模型的依赖比较强烈。

2.2 最大简约法

最大简约法是基于奥卡姆剃刀原则 （Occam's razor）而发展起来的一种进化树重构的方法，即突变越少的进化关系就越有可能是物种之间的真实的进化关系，系统发生突变越少得到的系统发生结论就越可信（Sober，1988）。最大简约法首先是由Camin & Sokal （1965）提出来的，经过 H ein （1990，1993）的研究发展使得用最大简约法来建立进化树得到极大的发展及应用。

最大简约法采用5个假设 （Felsenstein，1978，1979，1981a,b）：（1）序列中的每个位点独立进化；（2）不同世系（lineage）独立进化；（3）序列上的位点（碱基或氨基酸）的替换概率小于该分枝系统发生时间的长度；（4）系统发生的不同分支改变有不同，但高变化率的分支和低变化率的分支间的变化大小不会相差很大；（5）位点间变化不会相差太大。一个位点的删除和插入各算一个变化，当然连续的删除 N 个位点，应该算作独立的 N 个事件。

用简约法推断系统发生关系，首先判断信息位点。信息位点是那些产生突变能把其中的一棵树同其他树区别开来的位点。如果一个位点是信息位点，那么该位点至少有两种以上的核苷酸，并且每种核苷酸至少出现两次（见表6）。简约法中只考虑信息位点而不考虑非信息位点。

其次确定每棵树的替换数目 （Fitch，1971）。这里以3棵树为例来说明构建过程，如图5。要确定每棵树的替换数目，就要从 5 个已知的外部节点上的核苷酸推断出 4 个内部节点上最可能的核苷酸。寻找内部节点的算法如下：如果一个内部节点的两个直接后代节点上的核苷酸的交集为非空，g那么这个节点的最可能的候选核苷酸就是这个交集；否则为它的两个后代节点上核苷酸的并集。当一个并集成为一个节点的核苷酸集时，通向该节点的分支的某个位置必定发生一个核苷酸替换。故而并集中核苷酸的数目也是生成外部节点上的核苷酸的最小替换数，外部节点从它们的共同祖先出发，通过这些替换，形成当前的核苷酸状态。找好内部节点后，即可计算该内部节点后代的替换数。计算信息位点的替换数，是通过计算外部节点上不同核苷酸的数目减去 1 即可得到。考虑所有可能的树，分别对每棵树中的变化打分，统计每个位点的核苷酸最小替换数目，所有信息位点替换数的总和最小的树即为最简约树。

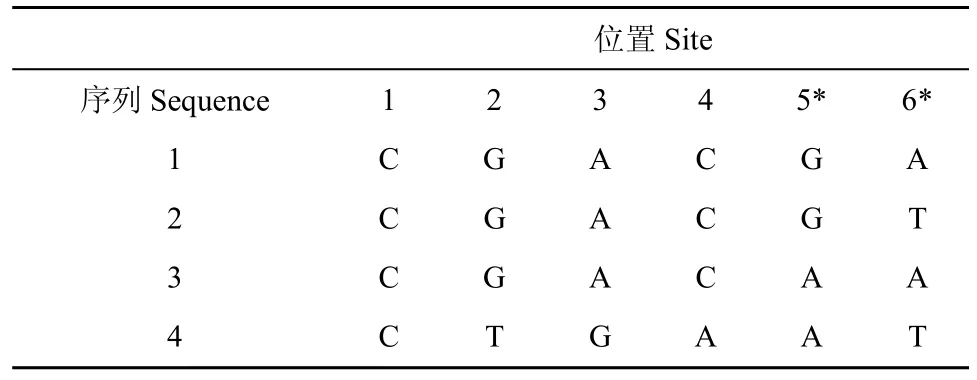
表 6 4条同源序列的比对Table 6 4 Homology sequences alignment

图 5 3 棵有根树及内部节点Figure 5 Three rooted trees and internal nodes

随着序列数量的增加，可能的树的拓扑结构呈现爆炸性增加 （如10 个物种，存在34 459 425 棵可能的无根树[，遍历这些可能的树的拓扑结构，计算出最小替换数而找到最简约树，无疑计算量是相当庞大的。对序列数据集较多的建树，一般选用分支约束算法 （branchand-bound algorithm）（Land & Doig，1960）和启发式算法 （heuristic algorithm）（Mucherino & Seref，2009）进行树的拓扑结构查找。

分支约束算法查找的树，首先是从只有两个物种组成的树开始 （如果是无根树，从3个物种的树开始）；其次程序试着在合适的位置增加下一个物种，并对增加物种后的树进行替换数目的评价，迭代直到将所有的物种都加到树上。它是一个深度优先搜寻的过程 （depth-first search）（Even & Even，2011）。首先把第三个物种加在第一个可能的位置，这时第四个物种加在它的第一个可能的位置，再次是第五个物种，依次遍历直到树的第一个可能的树产生。对树的步数进行衡量。改变物种的位置，直到遍历所有的位置。四棵树的深度优先搜寻的过程如下：

首先建立两个物种的树：（A,B）

把C加到第一个可能的位置：（（A,B）,C）

把D加到第一个可能的位置：（（（A,D）,B）,C）

把D加到第二个可能的位置：（（A,（B,D））,C）

把D加到第三个可能的位置：（（（A,B）,D）,C）

把D加到第四个可能的位置：（（A,B）,（C,D））

把D加到第五个可能的位置：（（（A,B）,C）,D）

把C加到第二个可能的位置：（（A,C）,B）

把D加到第一个可能的位置：（（（A,D）,C）,B）

把D加到第二个可能的位置：（（A,（C,D））,B）

把D加到第三个可能的位置：（（（A,C）,D）,B）

把D加到第四个可能的位置：（（A,C）,（B,D））

把D加到第五个位置：（（（A,C）,B）,D）

把C加到第三个可能的位置：（A,（B,C））

把D加到第一个可能的位置：（（A,D）,（B,C））

把D加到第二个可能的位置：（A,（（B,D）,C））

把D加到第三个可能的位置：（A,（B,（C,D）））

把D加到第四个可能的位置：（A,（（B,C）,D））

把D加到第五个可能的位置：（（A,（B,C））,D）

如上所示，深度优先搜寻也只不过是另外一种一次产生所有可能的树的算法。即使物种数量中等，生成的可能树的数量也是非常大的。当然这种情况实际中是不会发生的，因为树会以一个特定的顺序生成，一些可能树的拓扑结构是不会产生的。分支约束算法也是由这些深度优先搜索步骤组成，只不过有一点改变，在树的构建过程中，部分树如 （A,（B,C））的步数也被衡量。增加物种，预测会增加的步数，取增加步数的位置为增加的物种所在位置。分支约束算法会计算增加物种后不变的位点数量和变化的位点数量。因而如果 A、B 和C 及根有20个可变的位点，且如果树（（A,C）,B）要求 24 步，当 D 增加有 8 个可变位点，那么，无论 D 加到哪个位置，最终的树都不会少于 32 步。如果发现树（（A,B）,（C,D））仅仅只有 30 步，那么我们就可以确定（（A,C）,B）上没有位置可以让 D 加上。分支约束算法会保留一个最简约树列表，这样就可以砍掉一部分，从而避免一些可能的特定的树的分支生成。因而分支约束算法能让我们不必生成所有可能的树而又能得到最简约的树，从而减少计算时间。

启发式搜索算法通过子树分支交换 （branch swapping），把分支嫁接到此步分析中找到的最好的那棵树的其他位置，而产生一棵拓扑结构和初始树相似的树 （见图6）。

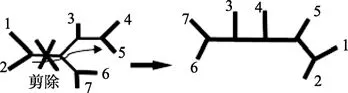
图 6 启发式搜索剪除与嫁接Figure 6 Pruning and grafting of heuristic search

对于有7条序列的启发式搜索在第一轮会产生上百棵新树，计算突变数总和，其中比初始树突变数更少的新树被保留并在第二轮分析中被剪除和嫁接。重复这个过程，直到无法再产生比前一轮总突变数更少的树，则此树为最简约树。启发式搜索能大大减少查找的可能树的数量，从而解决对大量数据搜索树的数量过大的问题。

最大简约法可能会产生多棵简约树，此时通常选取一棵能概括这些简约树的一致树（consensus tree）作为代表（Taylor et al，2011）。这种做法是将所有树中都一致的分支点作为二叉分支点，不一致的分支点变为连接多个分支的内部节点（如图 7）。

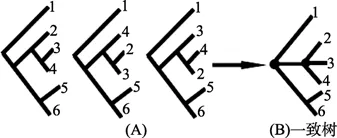
图 7 三个简约树对应的一致树Figure 7 Consensus tree form three MP trees

2.3 最大似然估计法

一般来讲，如果模型合适，最大似然法的效果较好。最大似然法根据特定的 “替代模型”（substitution model）分析既定的一组序列数据，使所获得的每一个拓扑结构的似然值最大。选出最大似然值最大的拓扑结构作为最优系统树。其分析的核心在于替代模型，常用的有 Jukes-Cantor 模型（Jukes & Cantor，1969），Kimura 双参数模型（Kimura，1980）等。算法要求所有分类单元有完整的 DNA序列数据 （如果有缺失则不计算），在运算过程中仅考虑碱基取代而忽略缺失/插入，算法相对费时。

在最大似然算法中，考虑拓扑结构和枝长两个参数，并对似然率求最大值来估计枝长。算法基于统计特性，有很好的数学理论支持。在进化速率可变的假设下，最大简约法略差于转换距离法和邻接法的结果，最大似然法的结果最优 （Zhong et al，2001）。也就是说极大似然算法允许各分支进化速率不同。极大似然算法原理如下：似然函数：给定进化模型 M，模型的 K 个参数，进化树拓扑结构，枝长，当前序列出现的可能性：如何取这些参数，使得该序列出现的可能性最大，

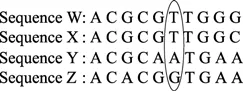
图8 4个DNA序列Figure 8 Four DNA sequences

图9 4个DNA序列可能的拓扑结构Figure 9 All possible trees come from four DNA sequences

因为有 3 个节点，每个节点可能的值是ATGC，所以有 43=64 个通路。

L（第6列）= SUM L （所有可能的进化路径）= L（路径1）+ L（路径2）+ L（路径3）+ … + L（路径64）

图 10中节点 1、2、3、4 为叶子节点，5、6 为内部节点，0 为根节点，vi为枝长，是进化树的参数，参数的值由似然函数通过观察到的序列来估计。节点 K 的似然函数：

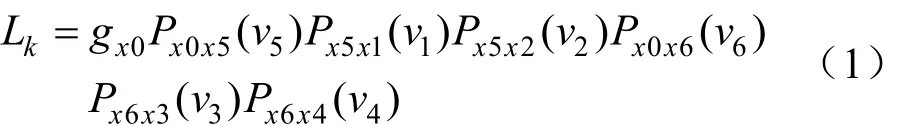
其中gx0表示节点 0 为核苷酸x0时的先验概率，常常等于核苷酸在整个序列中的相对频率，它可以用 ML 法来估计。Pij（v）为给定位点在时间0时的核苷酸 i 到时间 t 变为核苷酸 j 的概率，i、j 指 A、T、G、C 的任一种，在ML算法中允许各分支的替代速率 r 不同，用 vi=riti来表示第 i 个分支的预期替代数。计算 Pij（v）需要使用特定的替换模型。Felsenstein（Felsenstein，1981a）使用了等输入模型。在此模型中 Pii（v）和 Pij（v）为：

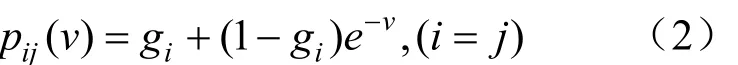
当 gi=1/4，v=4rt 时，上述模型演变为 Jukes-Cantor模型。针对不同类型的数据选择合适的模型可以增加准确度。以上过程分析了有根树的算法，如果使用一个可逆模型，即不论向前还是向后进化核苷酸的替代过程不变。用数学表述为：

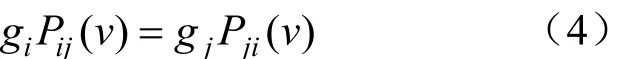
这样节点 5 和 6 之间的核苷酸替代数（v5+v6）恒定而与根节点 0 的位置无关。计算 Lk时，指定图 10 的 v5+v6为 v5，并假设进化开始于该树的某一点，为方便起见，假定从节点 5 开始，大大简化了树的复杂度，具体如图 11 所示。这样1 就可以简化为：（5）

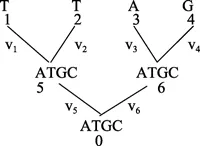
图10 TTAG可能的进化通路图Figure 10 The evolutionary pathway of TTAG

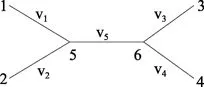
图11 有根树转为无根树Figure 11 Rooted tree into a unrooted tree

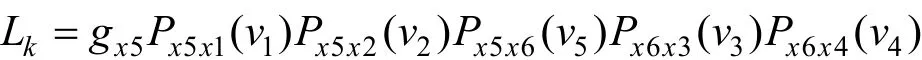
到此我们只考虑了一个核苷酸位点，在整个建树过程中我们必须考虑包括不变位点在内的所有核苷酸位点。整个序列的似然率 L 是对所有位点的 Lk求积，整个树的似然率对数为：

通过改变参数 Vi，使 lnL 最大化，计算方法可以使用 Newton 方法或其他数值计算方法实现。最后选出似然值最大的拓扑结构作为最优系统树。

2.4 贝叶斯算法

基于统计学规律运作的算法还有贝叶斯算法，与极大似然估计算法不同的是，后者指定树的结构和进化模型，计算序列组成的概率，从而推断出对应的进化树。前者正好相反，是由给定的序列组成，计算进化树和进化模型的概率。

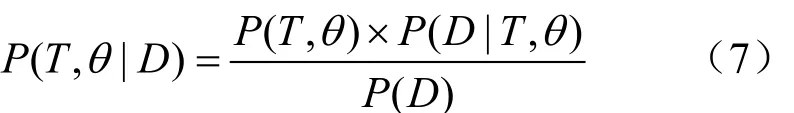
其中，P(T,θ) 为给定的树T和参数θ的先验概率/边缘概率，是不考虑序列时的概率。 P (T,θ|D)为给定序列下的后验概率， P (D |T,θ)为给定的树T和参数θ的似然值，分母P(D)是一正则化常数。该定理表明后验信息可由前验信息和碱

基序列信息所得（Yang & Rannala，2012）。具体原理如图 12 所示。

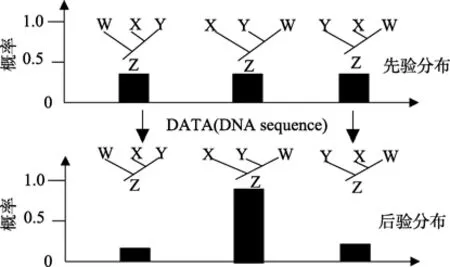
图12 贝叶斯算法进化树原理图Figure 12 Schematic of phylogenetic tree fromBayesian algorithm

开始不知道树的概率，先假设每棵树的可能性都是相等的，将 DNA 序列信息和进化模型代入贝叶斯公式计算每棵树的可能性，取概率最大者为最后的进化树。图12的拓扑中（X,（Y,W））的进化树概率最大，所以为最后的进化树。每个系统树的拓扑结构分布在不同区间；每棵树的位置受到拓扑结构及枝长的影响 （Sanmartín et al，2008）。对系统发生问题，难以得到各概率的解析解，现有的解决办法主要是 MCMC （Markov chain monte carlo sampling）方法。将进化树（拓扑结构与进化模型参数）转换为马尔科夫链，待马尔科夫链收敛于后验概率分布即可。

2.5 系统发育树重建常用的软件包介绍

目前有很多软件包可以进行系统发生树推断及可靠性检验，还有像Unifrac和ITOL（interactive tree of life）等在线画树和分析树的工具。网站http://evolution.genetics.washington.edu/phylip/softw are.html 列出了150多种相关软件包，并可以对软件进行按类别查询，如按软件的运行系统、使用的算法等进行查询，对软件进行简单介绍同时提供了下载的链接。具体使用时可按需求用不同的软件，这里简单介绍3种最常用的软件。

2.5.1 PHYLIP

PHYLIP （phylogeny inference package）是由美国华盛顿大学 Felsenstein 用 C 语言编写的系统发生推断软件包,它提供免费的源代码，支持Windows 和 Linux 等多种系统。在 3.69 版本中，由 35 个子程序组成，可以实现最大似然法、最大简约法和距离法建树。最大似然法有两类程序：带生物钟的建树子程序（dnamlk、promlk），可对进化似然距离进行估计；不带生物钟建树程序 （dnaml、proml）。最大简约法也有带分子钟建树子程序（dnapennys），可以对进化距离进行估计；和不带生物钟的建树子程序（dnapars、protpars）。距离法建树由 dnadist、prodist、fitch、kitsch、neighbor 等子程序组成，dnadist 和 prodist 可实现 F84、Kimura、Jukes-Cantor、LogDet 模型计算距离矩阵，fitch 子程序可实现不带分子钟的 Fitch-Margoliash法画树，而 neighbor 子程序带有邻接法和非加权组平均法两种画树方法。每种建树方法都带有各自许多不同的选项供研究人员根据自己研究的目的进行选择优化。软件包带有画树的子程序：可以画三角形有根树及矩形有根树（drawgram），也可以画无根树（drawtree）。子程序 seqboot 使用自举检验法或刀切法对构建的树进行标准误估计及可靠性检验，提供分析报告。此程序包还可以实现一致树的构建（consensus），以及树的重构（retree）等等。唯一不方便的是该程序包基于命令行形式，操作界面不够友好。

2.5.2 MEGA

MEGA（molecular evolutionary genetics analysis）是由美国宾夕法尼亚州立大学Masatoshi Nei 等编写的进行分子进化遗传分析的软件包。目前最新的版本为 5.0。它能对核酸序列及氨基酸序列进行系统发生分析。在建树方法上,提供了距离法中的非加权组平均和邻接法及 MP 法，5.0 版本还提供了最大似然法算法，对构建的树可进行自举检验及标准误估计的可靠性检验，并提供分析报告。该软件不仅可以对本地序列文件进行分析，而且可Web在线搜索分析，可以分析 NCBI 数据库中的序列文件来重建进化树。该软件可画出矩形、三角形、圆形等多种形状的系统发育树。

2.5.3 MrBayes

MrBayes （Bayesian inference of phylogeny）是由John Huelsenbeck 等编写，使用马尔可夫链方法来估计参数模型的后验概率分布。该软件采用命令行形式，支持 Windows 和 UNIX 等多种系统，能够处理核苷酸、氨基酸、限制性酶切位点和形态数据等多种数据，同时集成了多物种溯祖算法，支持正向、负向和总线形拓扑结构，支持 BEAGLE 数据库，在使用兼容的硬件（NVIDIA图形卡）条件下可以提高运行速度。表 7 列出了常用的建树软件及其特点。

当序列间的分歧度不高，且序列足够长时，邻接法、最大简约法和最大似然法得到的进化树往往具有相似的拓扑结构 （Saitou & Imanishi，1989）。当序列之间的分歧度比较高，将DNA序列转为距离矩阵时往往会丢失一些信息 （Penny，1982）。而距离法的性能依赖于距离矩阵的质量，因此，距离法只能当序列满足某些条件时才会有较高的准确性。简约法不依赖任何进化模型，但进化树的简约计分完全决定于重建祖先序列中的最小突变数，而突变是否按照事先约定的核苷酸最少替代途径进行是不得而知的。再者，所有分支的突变数不可能相同。由于没有考虑核苷酸的突变过程，使得长分支末端的序列由于趋同进化而显示较好的相似性，导致对“长枝吸引” （Holder & Lewis，2003）的敏感。因此，当序列分歧度较高时，最大简约法极可能得出错误的拓扑结构。最大简约法只适用于序列相似性较高的序列建立进化树，其次，最大简约法在序列数据量较大的时候，建立进化树相当耗时（是个 NP-complete 问题）（Foulds & Graham,1982）。最大似然法是一种建立在进化模型上的统计方法，具有统计一致性、健壮性，能够在一个统计框架内比较不同的树以及充分利用原始数据等优点 （Bryant & Galtier，2005）。但它与邻接法一样需要选择模型，一般选择 Kimura-2 参数模型。但对于不同模型会得出不同的结果，算法相对比较耗时，适用于序列不是很多的情况。贝叶斯法因为后验概率不仅涉及所有的树， 而且对于每一棵树还整合了枝长和替代模型参数值的所有可能组合，所以不可能采用常规的分析方法解决。所幸的是，一系列数值方法可用于近似地获取后验概率，其中最有用的就是马尔可夫链·蒙特卡罗算法。其基本思想是建立马尔可夫链，以替代模型参数作为状态空间，其静态分布就是参数的后验概率分布。通过计算机模拟和抽样技术获得分支格局的后验概率。同以往的最大似然法相比，贝叶斯推论的优越性在于：能够以很高的计算速度处理大型数据集，同时还使用后验概率衡量树的置信度 （Huelsenbeck &Ronquist，2001）。

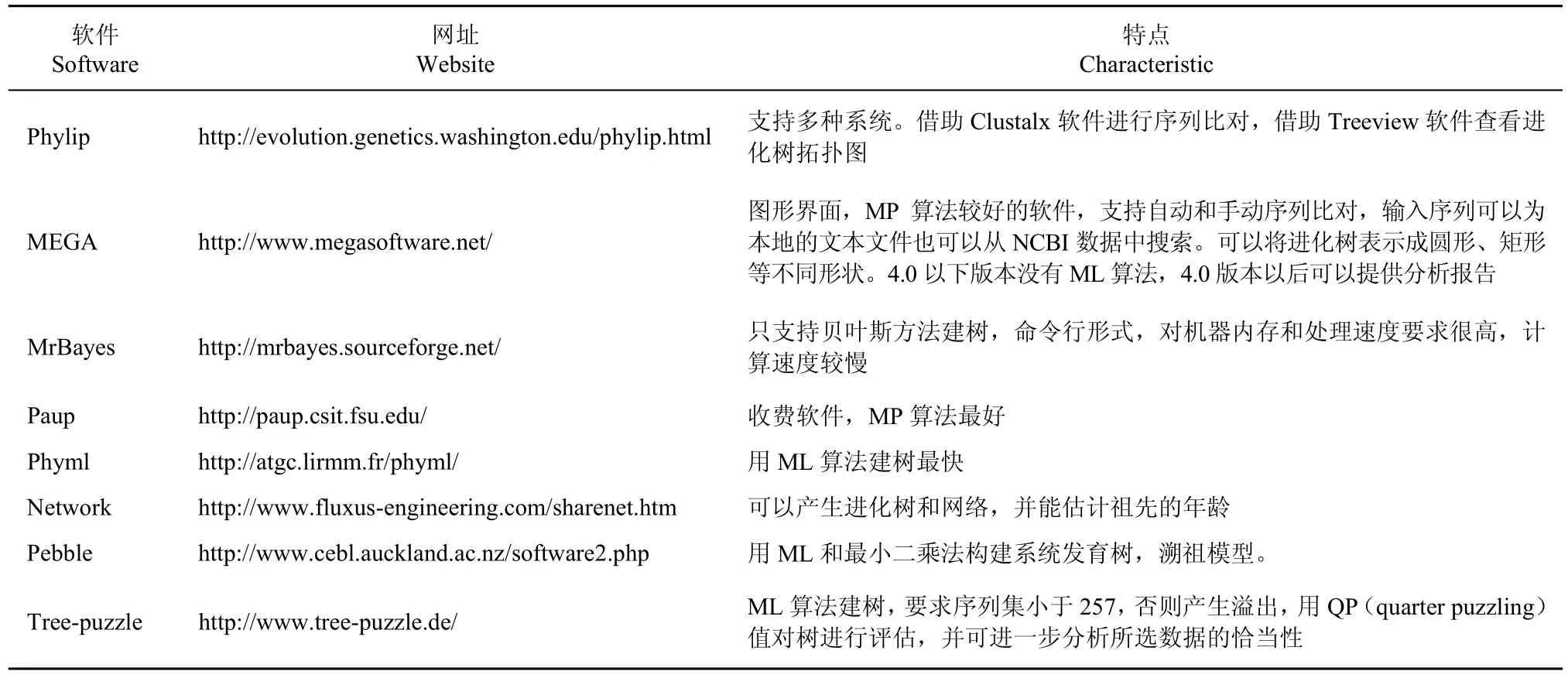
表7 常用软件及其特点Table 7 Frequently-used software and characteristic

3 总 结

近年人们在构建系统发育树方面已经取得了很大进展，构建系统发育树的算法和软件也一直在不断完善。通过对生物系统发生分析重建进化树，使人们更进一步了解了生命进化的历史。但构建系统发育树是一个复杂的任务，目前还没有哪一种算法能完全揭露真实的历史进化关系，同时现有算法存在的一些问题：如“长枝吸引”、非匀速分子钟的修正、搜索算法的优化等还有待进一步解决。系统发育分析的算法和软件的不断完善将会在更多的研究领域得到应用，如在基因多序列比对、分子钟以及统计系统地理学分析的过程中（Yang &Rannala，2012）。