超声速及高超声速壁板颤振中的湍流边界层效应

张 兵，韩景龙，钱 凯

（南京航空航天大学航空宇航学院，江苏 南京210016）

引 言

壁板颤振是壁板结构在高速气流中产生的一种自激振荡现象，属于典型的流固耦合问题。几乎所有的高速飞行器的蒙皮都属于壁板结构，发生壁板颤振会引发结构疲劳破坏，给飞行器安全带来严重威胁。在过去的几十年中，国内外学者已经就壁板颤振问题开展了大量研究［1～3］，但到目前为止，和试验结果完全一致的分析结果还很少见［4］。其原因在于影响壁板颤振的因素较复杂，使得试验条件难以准确模拟。

早在1963年，Fung就指出在壁板颤振的诸多影响因素中，湍流边界层厚度效应是计算结果和试验不一致的主要原因［5］。后来Muhlstein等专门进行了低超声速（马赫数1.0～1.4）条件下不同湍流边界层厚度壁板颤振的试验研究，结果表明随着马赫数增加，湍流边界层厚度对颤振边界影响逐渐增大，并在马赫数为1.2时达到最大，而后随马赫数增加而迅速减小［6］。Dowell通过求解线性扰动方程来计算表面压力场，并通过假定法向速度分布满足1／7次方指数率来模拟边界层，其计算结果和试验结果也存在较大误差［7］。近年来，随着CFD技术的发展，CFD／CSD耦合分析方法逐渐成为解决流固耦合问题的主要手段。Friedmann和Zhong Xaolin等曾分别采用三阶活塞理论、Euler以及N－S方程对给定运动的二维壁板进行对比计算，计算马赫数为10.05［8］。结果发现Euler方程和三阶活塞理论的气动力十分吻合，但采用N－S的结果与二者有着本质的不同，并给出了高超条件下气动力模型需要进一步考核的结论。随后，Bendisken，Gordnier，Selvam先后采用了CFD方法对跨声速、超声速壁板颤振问题进行研究，对比了无粘和粘性结算结果，但缺少试验验证，且没有针对边界层效应进行讨论［9～12］。最近，Atsushi等采用 CFD方法以及基于von Kármán板理论的有限元方法对Muhlstein等的试验模型进行了计算［13］，得到了和试验一致的结果，证明了采用 RANS（Reynolds－Averaged Navier－Stokes equations）方程可以获得较准确的气动力，但该文计算最大马赫数为2.4，并未考虑高超声速情形。因此，对于高超声速壁板颤振问题，有必要采用能反映流场粘性特征的N－S方程来开展研究。

本文通过采用求解RANS方程实现非定常气动力计算，并和结构有限元分析软件耦合实现壁板颤振时域计算。建立和文献［6］相同的壁板颤振模型，首先计算低超声速下不同湍流边界层厚度的颤振边界，并和试验结果进行比较验证；然后将计算方法推广到高超声速，分析壁板颤振中的湍流边界层效应，探讨其作用机理。

1 计算方法

基于CFD／CSD的流固耦合计算分主要包括3部分：结构分析、气动力计算、载荷及位移插值。下面介绍本文采用的方法。

1.1 基于有限元方法的结构动力学计算

以前研究较多采用von Kármán板理论对结构进行建模，考虑到目前结构动力学分析的有限元方法已经较为完善，以ANSYS，NASTRAN为代表的通用有限元分析软件可以完成包含材料非线性、几何大变形等非线性因素在内的结构分析。本文采用ANSYS软件来实现结构计算。

采用有限元方法对壁板结构进行离散，其动力学方程为

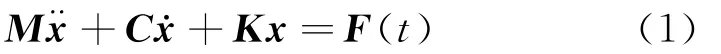
式中x为节点自由度向量，M为质量矩阵，C为结构阻尼矩阵，K为结构刚度矩阵，F为载荷向量。当存在几何非线性效应时，刚度矩阵K不再是常数矩阵，而是自由度x的函数，需要采用迭代法求解。在ANSYS中采用全瞬态分析，开启大变形非线性效应，计算过程采用Newmark方法进行时间推进。

1.2 基于CFD方法的气动力计算

采用迎风格式的有限体积方法是目前CFD计算的主流方法，本文采用自主开发的基于上述方法的三维N－S方程求解程序来实现气动力计算。采用有限体积方法离散后的N－S方程为

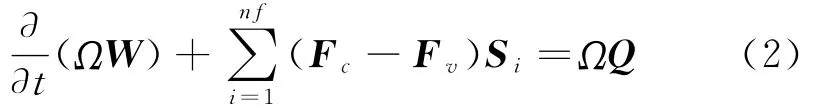
式中Ω为控制体体积，W为控制体守恒变量，Fc和Fv分别为控制体第i个面上的对流通量和粘性通量，Q为控制体源项，Si为控制体第i个面的面积向量，nf为控制体面的个数。

为了精确捕捉激波，方程（2）中的对流项采用Roe格式，并通过MUSCL插值使空间离散精度达到二阶。粘性通量采用二阶中心差分格式计算。

时间离散方法采用二阶Euler向后差分格式，如下式

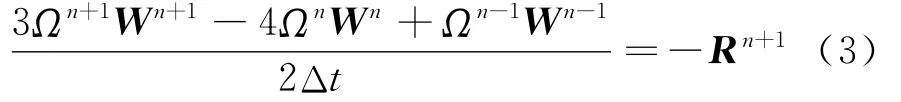
式中 上标表示时间步序号，Δt为时间步长，R为右端残值项，形式如下

采用Newton－Raphon方法求解非线性方程（3），通过将Wn＋1在Wn处线性化，并引入伪时间步得到隐式时间格式

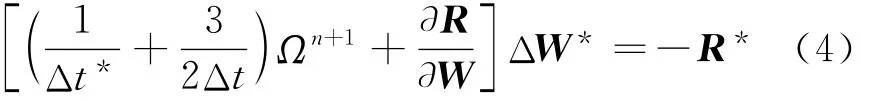
式中 上标＊表示伪时间步。每一个伪时间步采用LUSGS方法求解。

由于流体方程是采用Euler描述法，而结构则采用Lagrangian描述法，因此对于包含网格运动的N－S方程其对流通量需要采用Arbitary Lagrangian Eulerian（ALE）公式计算

式中Vt为控制体面的运动速度。

此外为了减小时间离散误差，控制体体积、面积矢量、面运动速度还需满足几何守恒率［14］。

为准确计算湍流边界层，湍流模型选取Menter’s SST两方程剪切应力模型［15］，考虑到高超声速高雷诺数的特点，能量方程中需要包含湍流动能部分，此外湍流方程和质量、动量及能量方程全耦合求解。为避免驻点处湍流动能的累计误差，湍流动能方程求解过程中的需要对产生项进行限制，本文取小于10倍的耗散项。

1.3 耦合计算平台及计算流程

数据传递、载荷插值及迭代计算方法是耦合计算的3个关键问题。为了避免传统I／O数据传递方式的效率瓶颈，本文在自主开发的基于共享内存的多场耦合计算平台上进行多个软件之间的数据交互［16］。

载荷插值精度直接决定了计算结果的精度，常用的载荷插值方法有样条插值、形函数插值、守恒插值等。考虑到本文计算模型较简单，结构网格节点和流体网格节点采用一对一形式，这样可以避免由边界载荷及位移差值带来的计算误差。

耦合计算流程依据耦合特点可分为松耦合、紧耦合两种，松耦合方法各个物理场边界条件采用另一侧上个时间步的值，Gordnier曾指出这种两个物理场间的不同步，在长物理时间计算中会引起较大累积误差，建议采用紧耦合方式计算［10］。紧耦合方式需要在一个时间步对结构和流场进行内迭代求解来满足时间步上的一致，其缺点是计算量较大，本文采用紧耦合方法计算。

2 计算模型

2.1 结构模型

计算结构模型如图1所示，为周边固支的矩形板。其中，a＝0.228 6m 为壁板沿流向尺寸，b＝2a为壁板展向尺寸，h＝0.001m为板厚度。结构材料为AZ31B－H24镁合金，密度为1 762kg／m3，弹性模量为40.5GPa，泊松比为0.35。

图1 壁板结构示意图Fig.1 The panel structure model

ANSYS中采用SHELL63单元，结构沿流向和展向分别等距划分20×40单元。ANSYS模态分析结果见表1，计算结果的第4，5阶模态分别和试验的第5，4阶对应，这是由于试验边界并非完全固支的原因［6］。

表1 壁板结构模态的仿真结果Tab.1 Results of panel structure modal analysis

图2 壁板结构模型前5阶阵型图Fig.2 First five mode shapes of panel structure

板内压取流场初始计算结果作用力的平均值，为了激发壁板振动，在结构所有节点施加初始z方向3m／s的速度扰动。

2.2 流场网格及边界条件

流场计算区域如图3所示，流体网格一共分为12个结构网格块，流场沿x，y，z三个方向的网格节点数为111×81×81，壁面第一层网格高度为1.0×10－6m，法向网格增长率为1.1。板所在平面（z＝0）内各个面均为绝热壁面，为了防止入口处奇异，在距离入口0.1a距离的面设置为对称面。其余各个边界设置为超声速远场。

图3 流场计算区域示意图Fig.3 Computational domain of flow－field

边界层厚度通过改变壁板前方到对称面距离l来调整，其值取板中心位置处的厚度值，计算公式采用速度边界层厚度公式

式中U为流体速度，U∞为来流速度。

3 计算结果

3.1 超声速壁板颤振验证

计算来流条件采用试验值［6］，马赫数范围为1.05～1.4，时间步长取0.000 1s，最大子迭代步取6，子迭代步收敛残差为0.01。结果中的颤振无量纲动压由下式计算

式中υ为材料泊松比，Es为弹性模量，ρ∞为来流密度，U∞为来流速度。

3.1.1 Euler方程计算结果

图4 Ma＝1.2时板中心点垂直位移响应时间历程Fig.4 Vertical displacement response history of the center point at Ma＝1.2

如图4为Ma＝1.2，λ＝105时的板中心点垂直方向无量纲位移（Δz／h）的时间历程，壁板颤振形态为极限环振荡，中心点的无量纲幅值为1.0，振动频率为116.3Hz。如图5为3个典型相位（中心点位值、零、最大值的3个相位的边界层无量纲速度云图，其中x值坐标范围0～0.228 6为壁板，0.98的等值线为边界层厚度。3个状态下边界层厚度基本不变化，但要超过来流厚度的10%，中心点的无量纲颤振幅值Δz／h在1左右，而边界层厚度为24倍的板厚，因此振幅和边界层厚度相比很小。

考虑板的振动位移，板中心点的边界层厚度在一个周期内的变化规律相当于幅值为Δz的正弦运动，此时，边界层起到了振动抑制的作用。

图8所示为马赫数1.2时无量纲颤振动压随边界层厚度的变化曲线，为了便于比较，将Euler方程移分别为最小值、零和最大值）壁板表面的无量纲位移分布图，由位移图及频率值可知，颤振主模态发生在一阶，这与文献［7］的结论吻合较好。

图6为颤振边界随马赫数的变化曲线，本文计算结果和文献［7］结果一致，和试验值吻合较好［6］。马赫数为1.4时的颤振边界和试验值差别较大，是由于试验结构边界并不是完全固支，可以从结构模态计算结果看出。

图5 Ma＝1.2，λ＝105时3个相位的壁板表面位移分布Fig.5 Panel displacement contours of three typical phases at Ma＝1.2，λ＝105

图6 采用Euler方程的颤振动压计算结果Fig.6 Flutter dynamic pressure results using Euler euqations

图7 Ma＝1.2，λ＝180时3个典型相位的无量纲速度云图Fig.7 Dimensionless velocity contours of three typical phases at Ma＝1.2，λ＝180

图8 Ma＝1.2时颤振动压随边界层厚度变化曲线Fig.8 Flutter dynamic pressure varying with boundary layer thickness at Ma＝1.2

3.1.2 N－S方程计算结果

通过求解RANS实现气动力计算，计算了马赫数为1.2时不同边界层厚度下的壁板颤振动压。图7所示为λ＝180，δ／h＝0.11时中心点位移为最小的计算结果（δ＝0）也标记在图中。其中空心圆点数据点为按照试验结果外插得到的无粘结果。结果表明本文结果和试验吻合较好，马赫数为1.2时，边界层厚度对颤振动压影响非常大。当边界层的无量纲厚度为0.1时，考虑边界层效应的计算颤振动压超过无粘结果的160%。

3.2 高超声速壁板颤振

试验中的来流马赫数最大为1.4［6］，并未考虑高马赫数下的情况，文献［13］也仅计算到马赫数为2.4。为考察高马赫数下的边界层效应，计算马赫数选取了2.0，4.0，6.0，8.0四个工况，不考虑真实气体效应，壁面按照绝热壁面考虑，来流温度为288 K。

如图9结果为边界层无量纲厚度δ／h＝0.087，Ma＝8.0，Δz／h＝1，λ＝4 806时的3个典型相位的无量速度云图，由图可知边界层厚度基本保持不变。中心点位移为最小值、零、最大值的3个典型相位的位移如图10所示，其运动形态上和图5所示的低超声速有较大不同。

图9 Ma＝8，λ＝4 806时3个典型相位的无量纲速度云图Fig.9 Dimensionless velocity contours of three typical phases at Ma＝8，λ＝4 806

图10 Ma＝8，λ＝4 806时3个典型相位的无量纲位移云图Fig.10 Dimensionless displacement contours of three typical phases at Ma＝8，λ＝4 806

图11 不同马赫数下N－S方程和Euler方程颤振动压结果对比Fig.11 Comparison of flutter dynamic pressure at different Mach number using N－S and Euler equations

图12 N－S方程和Euler方程结果差别随马赫数变化曲线Fig.12 Result difference varying with Mach number using Euler and N－S equations

如图11为马赫数为所有工况的结果比较图，马赫数超过2.0时，Euler方程和N－S方程的颤振动压结果在绝对值上差别逐渐增大。图12为二者结果的相对差别，马赫数超过2后，相对差别基本保持在20%左右，且这个差别基本不随马赫数变化。高马赫数下，采用N－S方程的计算颤振动压高于Euler结果，此时边界层主要起到了振动抑制的作用，在一定程度上提高了颤振稳定性。

4 结 论

（1）针对文献［6］壁板颤振试验模型，通过求解RANS方程实现气动计算，和ANSYS软件耦合实现壁板颤振的时域计算，计算结果和试验值吻合较好，表明本文计算模型正确，计算方法精度较高。

（2）计算结果表明低超声速阶段湍流边界层厚度对壁板颤振影响显著，边界层无量纲厚度为0.1时，其颤振动压和Euler结果相比，差别最高可达160%，和试验结果吻合较好。

（3）高超声速情况下，边界层厚度对颤振动压仍有较大影响，其差别维持在20%左右，基本不随马赫数变化。湍流边界层总体上起到了提高系统稳定性作用。因此准确预测壁板颤振问题，边界层效应是必须考虑的因素。

［1］ Dowell E H.A review of the aeroelastic stability of plate and shells［J］.AIAA Journal，1970，8（3）：385—399.

［2］ Mei C Abdel－Motagaly K，Chen R.Review of nonlinear panel flutter at supersonic and hypersonic speeds［J］.Applied Mechanics Reviews，1999，52（10）：321—332.

［3］ 杨智春，夏巍.壁板颤振分析模型、数值求解方法和研究进展［J］.力学进展，2010，40（1）：81—98.Yang Zhichun，Xia Wei.Analytical models，numerical solutions and advances in the study of panel flutter［J］.Advances in Mechanics，2010，40（1）：81—98.

［4］ Dowell E H.Theoretical and experimental panel flutter studies in the Mach number range 1.0to 5.0［J］.AIAA Journal，1965，3（12）：2 292—2 304.

［5］ Fung Y C.Some recent contribution to panel flutter research［J］.AIAA Journal，1963，1（4）：898—909.

［6］ Muhlstein L，Gaspers P A，Riddle D W.An experimental study of the influence of the turbulent boundary layer on panel flutter［R］.NASA TND－4486，1968.

［7］ Dowell E H.Generalized aerodynamic forces on a flexible plate undergoing transient motion in a shear flow with an application to panel flutter［J］.AIAA Journal，1971，9（5）：834—841.

［8］ Nydick I，Friedmann P P，Zhong Xiaolin.Hypersonic panel flutter studies on curved panels［R］.AIAA－95－1458，1995.

［9］ Davis G A，Bendiksen O O.Transonic panel flutter［R］.AIAA－93－1476，1993.

［10］Gordnier R E，Visbal M R.Development of a three－dimensional viscous aeroelastic solver for nonlinear panel flutter［J］.Journal of Fluids and Structures，2002，16（4）：497—527.

［11］Gordnier R E，Visbal M R.High－fidelity computational simulation of nonlinear fluid－structure interaction problems structure interaction problems［J］.The Aeronautical Journal，2005，109（7）：301—331.

［12］Selvam R P，Visbal M R，Morton S A.Computation of nonlinear viscous panel flutter using a fully－implicit aeroelastic solver［R］.AIAA－98－1844，1998.

［13］Atsushi H，Takashi A.Effects of turbulent boundary layer on panel flutter［J］.AIAA Journal，2009，47（12）：2 785—2 791.

［14］Thomas P D，Lombard C K.Geometric conservation law and its application to flow computations on moving grids［J］. AIAA Journal，1979，17 （10）：1 030—1 037.

［15］ Menter F R.Two－equation eddy－viscosity turbulence models for engineering applications［J］.AIAA Journal，1994，32（8）：1 589—1 605.

［16］张兵，韩景龙.多场耦合计算平台与高超声速热防护结构传热问题研究［J］.航空学报，2011，32（3）：400—409.Zhang Bing，Han Jinglong.Multi－field coupled computing platform and thermal transfer of hypersonic thermal protection structures［J］.Acta Aeronautica et Astronautica Sinica，2011，32（3）：400—409.