机载多管火箭系统振动特性研究

张 驰，芮筱亭，戎 保，王国平

（南京理工大学发射动力学研究所，江苏 南京210094）

引 言

多管火箭系统作为连射武器，其系统振动特性对其动态性能和射击密集度的影响非常大，系统振动特性的准确快速计算已成为多管火箭发射动力学的重要基础和核心内容之一。芮筱亭等对车载多管火箭振动特性进行了系列的研究［1～3］，为优化射序和射击间隔提高车载多管火箭射击密集度提供了重要支撑。

直升机机载多管火箭是一类新型多管火箭。准确计算机载多管火箭系统的振动特性，建立起机载多管火箭总体参数与系统振动频率之间的定量关系，合理匹配系统固有振动频率与射频，对保证机载多管火箭动态性能和射击密集度十分重要。通常力学方法在计算刚柔耦合多体系统固有振动特性时，需要建立系统总体动力学方程，不仅需要解决涉及的矩阵阶次高计算工作量大的困难，还可能面临计算“病态”问题。寻求机载多管火箭等复杂武器系统动力学建模和振动特性快速计算方法，是目前发射动力学问题的迫切需要。

多体系统传递矩阵法无需建立系统的总体动力学方程［4－7］，涉及系统矩阵阶次、计算量小、避免了刚弹耦合多体系统特征值问题的计算“病态”的特点，为解决复杂机载多管火箭武器系统振动特性快速计算问题提供了新手段。本文应用多体系统传递矩阵法，建立了某机载多管火箭武器系统动力学模型，从理论、计算、试验三方面研究了机载多管火箭武器系统的振动特性，实现了对机载多管火箭刚弹耦合系统的固有振动特性的快速计算，理论计算得到了模态试验的验证，为科学评价机载多管火箭武器系统动态性能和提高密集度奠定了基础。

1 机载多管火箭系统动力学模型

应用多体系统传递矩阵法，根据机载多管火箭各个部件的自然属性，将它们分别视为集中质量、刚体、弹性梁、扭簧、弹簧等力学元件，如图1所示。将任一瞬时机载多管火箭中除去已击发火箭弹和最新击发火箭弹所在火发器简称火发器，除去火发器的挂架部分简称挂架部分，除去轮子的直升机简称机体，最新击发火箭弹所在定向管尾部简称定向管尾，并将它们视为各具有6个自由度的刚体；3个轮子视为各具有3个自由度的集中质量；最新击发火箭弹所在定向管简称定向管并视为空间运动弹性梁；定向管与火发器之间的作用以及挂架与火发器的弹性和阻尼效应、轮子的弹性和阻尼效应及与地面的作用、挂架与定向管间的联接等，分别用反映3个方向相对角运动的扭簧和反映3个方向相对线运动的弹簧及与之并联的阻尼器来等效。

本文以机载多管火箭地面停放状态为例，直升机旋翼下洗流对火箭弹的影响等效为纵风，地面支撑作为系统的边界条件包含在系统模型之中。其他状态的机载多管火箭动力学模型与此类似，如悬停状态时的机载多管火箭系统动力学模型可以在地面支撑下的机载多管火箭动力学模型的基础上，忽略地面支撑，将直升机运动参量作为发射系统外部激励，同时考虑直升机旋翼下洗流对火箭弹弹道特性的影响。

根据“体”和“铰”统一编号的原则，地面边界编号为0；3个轮子与地面联接的弹簧及与之并联的阻尼器依次编号为1，2，3；3个轮子依次编号为4，5，6；3个轮子与机体联接的弹簧及与之并联的阻尼器依次编号为7，8，9；机体、回转部分、起落部分依次编号为10，12，14；元件10与元件12间的联接作用以及元件12与元件14间的联接作用的扭簧和弹簧及与之并联的阻尼器分别编号为11，13；挂架与第i个定向管间的两处联接扭簧和弹簧及与之并联的阻尼器分别编号为9＋7i，11＋7i；第i个定向管的后端面自由边界编号为7＋7i；第i个定向管尾部编号为8＋7i；第i个定向管与挂架的前联接点与后联接点之间的部分编号为10＋7i，前联接点前面的部分编号为12＋7i；第i个定向管的前端面自由边界编号为13＋7i。即地面支撑下的机载多管火箭系统动力学模型为：由各种铰相联接的3个刚体、19个弹性体和3个集中质量组成的刚弹耦合多体系统。

图1 机载多管火箭武器系统动力学模型Fig.1 Dynamics model of airborne multiple launch rocket systems

2 机载多管火箭系统振动特性计算方法

本节基于多体系统传递矩阵法，建立机载多管火箭系统振动特性快速计算方法，以实现对机载多管火箭系统的固有振动特性的准确分析。

2.1 状态矢量

应用多体系统传递矩阵法，定义机载多管火箭武器系统各联接点处的状态矢量如下：

类似。Z4－6，1－3，Z4－6，7－9的定义与Z0，1－3类似。

式（1）～（4）中，Zi，j第1个下标i是体元件的序号，第2个下标j是铰元件的序号。用X，Y，Z表示线位移对应的模态坐标列阵；Θx，Θy，Θz表示角位移对应的模态坐标列阵；Mx，My，Mz表示内力矩对应的模态坐标列阵；Qx，Qy，Qz表示内力对应的模态坐标列阵。

2.2 机载多管火箭系统部件传递矩阵

本文给出了定向管的传递矩阵，限于篇幅，其他元件的传递矩阵的详细推导过程可参见文献［4］。把定向管作为空间运动梁来处理，只考虑梁的横向振动，不计其纵向和扭转振动，可得点（10＋7i，9＋7i）到点（10＋7i，11＋7i）的传递方程

式中 第i个定向管上点（10＋7i，9＋7i）到点（10＋7i，11＋7i）的传递矩阵U10＋7i可表示为

在安全设计阶段，通常要根据气体不同的性质，在场所中设置相应的气体浓度报警仪。一旦发生泄漏，现场气体浓度报警仪将立即启动声光预警，有效缩短应急时间。同时，针对涉氨和易燃气体的场所，应设置用于消防灭火和液氨泄漏稀释吸收的消防喷淋系统，并与场所内气体泄漏报警仪联锁。当局部气体浓度达到安全预警值时，气体泄漏报警仪发出声光报警的同时，联锁自动喷淋控制阀开启，消防水通过管道和喷淋头喷洒水雾，有效吸收氨气和灭火，避免突发情况下事故进一步扩大。

式中S，V，U，T为 Крылов函数［8］，

l为梁的长度，EI为梁的抗弯刚度，为线质量密度。

2.3 机载多管火箭系统总传递方程

由多体系统传递矩阵法，拼装各部件的传递方程，可得机载多管火箭系统的总传递方程

式中 系统边界点的状态矢量

机载多管火箭系统总传递矩阵

Uall为21×42矩阵。

2.4 机载多管火箭系统特征方程

记去掉Uall中第1，2，3，7，8，9，13，14，15，25，26，27，28，29，30，37，38，39，40，41，42列得到21×21方阵。则式（6）可表示为

式（11）即为机载多管火箭的特征方程。求解机载多管火箭的特征方程（11），即可得机载多管火箭系统的固有振动频率ωk（k＝1，2，3，…）。求得机载多管火箭系统的固有振动频率ωk（k＝1，2，3，…）后，在给定的归一化条件下（如令b的21个元素中绝对值最大的元素等于1），求解方程（10）可得到对应于固有振动频率ωk的b和Zb，即对应于固有振动 频 率ωk的 状 态 矢 量Z0，1－3，Z8＋7i，7＋7i和Z12＋7i，13＋7i。进而通过传递方程得到对应于ωk的全部联接点和定向管上任一点的状态矢量。

基于上述理论方法，建立了机载多管火箭系统振动特性数值仿真系统。

3 机载多管火箭振动模态试验

建立直升机机载多管火箭振动模态测试方法，对某直升机机载多管火箭系统进行了振动模态试验，测量了其在满载和空载及不同装弹情况下的固有振动频率、振型、阻尼比等模态参数，为验证本文所建动力学模型、所选参数和振动特性仿真系统的正确性提供了重要依据。试验采用冲击激励的方法激发直升机机载多管火箭系统的振动，选取直升机机载多管火箭系统尾部第60点为激励点，同时选用丹麦B＆K的高灵敏度加速度传感器4370测量直升机机载多管火箭系统的振动响应。直升机机载多管火箭系统模态试验框图和模态试验测点分布分别如图2和3所示。机载多管火箭系统满载垂向第1阶模态振型如图4所示。

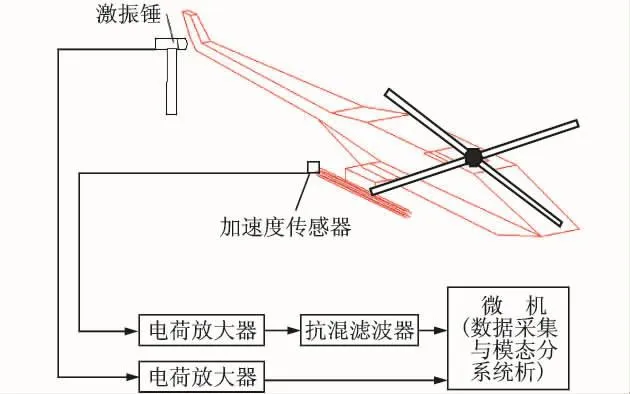
图2 机载多管火箭系统模态试验框图Fig.2 Modal test chart of airborne multiple launch rocket systems

图3 机载多管火箭系统模态试验测点分布图Fig.3 Distribution of test position for modal test of airborne multiple launch rocket systems

图4 机载多管火箭系统满载垂向第1阶模态振型Fig.4 The first modal shape got by modal test of airborne multiple launch rocket systems

4 机载多管火箭系统振动特性分析

根据本文建立的机载火箭系统的传递方程、传递矩阵和特征方程，依据工程获取的机载多管火箭各部件的结构参数和联接参数，求解建立的机载多管火箭特征方程，即可得到机载多管火箭系统任意装填情况下的振动特性。对于振动系统每个ωk（k＝1，2，3，…），由系统的传递方程可得机载多管火箭系统任意点的状态矢量。用上述方法，实例数值仿真了某机载7管多管火箭系统的固有振动特性。在Pentium Dual 2.2 GHz的计算机上只需21 s的时间即可计算完从满载到空载8种工况下的振动特性。表1和2分别给出了满载情况和空载情况下前10阶固有频率的计算与试验结果的对比。对比表明，两者吻合较好，验证了本文理论方法的正确性。从表1和2可以看出，应用本文方法，能够快速计算机载多管火箭从满载、逐发射击到空载各工况下系统振动特性，可较为精细刻画由于火箭弹射击后整个机载多管火箭质量等参数发生变化后振动特性的变化，为优化射序和射击间隔提供了重要参数。

表1 满载情况下频率仿真与试验结果对比Tab.1 Test and simulation results of natural frequencies of full load rockets

表2 空载情况下频率仿真与试验结果对比Tab.2 Test and simulation results of natural frequencies of non load rockets

5 结 论

本文应用多体系统传递矩阵法，建立了某机载多管火箭系统动力学模型，从理论、计算、试验三方面研究了机载多管火箭系统的振动特性，对某机载多管火箭系统的固有振动特性进行了数值仿真，实现了对机载多管火箭刚弹耦合系统的固有振动特性的快速计算，理论计算得到了模态试验的验证，为优化射序和射击间隔提高多管火箭射击密集度提供了关键数据。本文方法具有无需建立系统总体动力学方程、涉及系统矩阵阶次、计算速度快等优点，可用于各种机载多管火箭、机载火炮等系统振动特性分析。

［1］ 芮筱亭，陆毓琪，王国平，等.多管火箭发射动力学仿真与试验测试方法［M］.北京：国防工业出版社，2003，12—130.RUI Xiao－ting，LU Yu－qi，WANG Guo－ping，et al.Simulation and test methods of launch dynamics of multiple launch rocket system［M］.Beijing：National Defense Industry Press.2003，12—130.

［2］ 唐静静，芮筱亭，陆毓琪，等.自行火炮振动特性的计算［J］.弹道学报，2003，（2）：23—27.TANG Jing－jing，RUI Xiao－ting，LU Yu－qi，et al.Calculation of the self－propelled artillery vibration characteristics［J］.Journal of Ballistics，2003，（2）：23—27.

［3］ 芮筱亭，王国平，贠来峰，等.某远程多管火箭振动特性研究［J］.振动与冲击，2005，24（1）：9—12.RUI Xiao－ting，WANG Guo－ping，YUN Lai－feng，et al.Study on the vibration characteristics of LRMLRS［J］.Journal of Vibration and Shock，2005，24（1）：9—12.

［4］ 芮筱亭，贠来峰，陆毓琪，等.多体系统传递矩阵法及其应用［M］.北京：科学出版社，2008，139—202.RUI Xiao－ting，YUN Lai－feng，LU Yu－qi，et al.Transfer matrix method of multibody system and its applications［M］.Beijing：Science Press，2008，139—202.

［5］ RUI Xiao－ting，WANG Guo－ping，LU Yu－qi，et al.Transfer matrix method for linear multibody system［J］.Multibody System Dynamics，2008，19（3）：179—207.

［6］ RUI Xiao－ting，YUN Lai－feng，WANG Guo－ping，et al.Augmented eigenvector and its orthogonality of linear multi－rigid－flexible－body system ［J］.Journal of China Ordnance，2008，4（2）：100—105.

［7］ RONG Bao，RUI Xiao－ting，WANG Guo－ping，et al.Modified finite element transfer matrix method for eigenvalue problem of flexible structures［J］.Journal of Applied Mechanics，2011，78（2）：021016.1—021016.7.

［8］ ［苏］H M巴巴科夫著，蔡承文等译.振动理论［M］.北京：人民教育出版社，1963.CAI Cheng－wen.Vibration Theory［M］.Beijing：People＇s Education Press，1963.