空间光滑活动模型在东部海域地震危险性评价中的应用*
张力方,吕悦军,兰景岩,谢卓娟
0 引言
目前我国地震区划的技术方法是划分潜在震源区的地震危险性概率分析方法 (高孟潭,卢寿德,2006)。该方法最关键的技术环节是根据地震地质构造和历史地震活动性,划分潜在震源区和确定地震活动性参数,要求研究区域内地震地质构造清晰 (胡聿贤,1999)。但对于地震构造研究还不够深入或地震活动具有弥漫性的地区,采用该方法评价地震危险性势必会带来较大的不确定性。
1995年,由于当时对美国中东部地震潜源了解很有限,Frankel(1995)以地震目录作为唯一输入数据,先将研究区域网格化,在每个网格内统计地震活动率,再将累计地震活动率用圆形高斯光滑函数处理,最后以点源模型评价地震危险性。如此处理将潜源简化为小方格单元简单易行,因此在世界各国地震危险性分析中得到了广泛应用(Lapajne et al,2003;Pelaez Montilla et al,2002;杨勇等,2008)。圆形空间光滑模型符合普遍认同的原地复发原理,即未来中强震发生在历史地震附近。它的优点是在保持地震数目不变的情况下,以相关距离抵消了地震地位误差,又充分体现了地震活动的空间非均一性。但是在地震活动模型中仅体现原地复发原理还不够,因为未来地震活动的空间分布往往与构造断裂有一定的空间相关性,这就需要在建立地震空间光滑模型时需要考虑到相关地震构造因素。于是Lapajne等(2003)对该方法进行了改进,采用断层导向性的椭圆光滑方法,使评价地震活动性参数更加合理。
我国拥有广阔的大陆架,含有较为丰富的油气资源。自20世纪80年代以来,我国海洋石油探测和开发速度加快,在渤海、黄海、东海和南海等海域已建成100余座海上石油平台,今后5年还将建设100余座海上石油平台,海洋石油已成为我国重要的原油生产基地 (刘光鼎,2007)。除了海上石油平台和海底输油 (气)管道工程外,在海域及滨海地区其他建设工程的种类和数量也越来越多,如海底通讯设施、跨海大桥、人工岛、港口码头、核电站等。我国海域历史上曾发生过7级或7级以上的地震,近期的中强地震活动也较频繁(汪素云等,1990;彭艳菊等,2008)。因此,海域的一些重大工程同样面临遭受较大的地震风险。
中国地震局先后编制了满足一般建设工程抗震设防要求的《中国地震烈度区划图 (1990)》、《中国地震动参数区划图 (2001)》。同时对各种大型建设工程,如高层建筑、大桥、大坝、核电厂及新的开发区等,已发展了不同类别的工程场地设计地震动参数的确定方法,并形成相关的技术规范和法规。但由于对海域地区地震构造信息掌握有限等客观原因的制约,海域内的地震区划研究尚属空白。因此,在目前掌握的有限资料情况下,如何进行有效的海域地震动区划研究,在海洋工程的建设中显得非常急迫。
本文以我国东海海域为研究对象,建立地震构造单元,依次采用基于地震目录的圆形光滑和断层导向性的椭圆光滑的地震活动模型,计算各网格点的地震发生率。选取合适的地震动衰减关系,利用网格源的地震危险性概率评价方法,尝试给出该地区地震区划结果,探索适合于海域地区的地震危险性性评估和震动区划研究工作方法。
1 总体评价方法介绍
首先根据区域地震构造背景和地震活跃水平等信息划分地震构造单元,确定各地震构造单元内的地震活动性参数,如主要断层性质、断层方位角及其权重、b值、震级上下限等。接着进行二阶的高斯空间光滑处理,采用基于地震目录的圆形高斯光滑过程,对网格内直接统计得到的地震发生率进行处理。再以建立的地震构造单元为基础,利用该区内主导断裂的性质、断层方位角及震级—破裂长度关系等建立断层导向性的椭圆光滑模型,进行二次光滑处理,得到网格点的地震年平均发生率。最后采用适当的地震动衰减关系,计算该区域地震危险性结果 (PGA)。
2 空间光滑方法
2.1 圆形空间光滑
Frankel(1995),王健 (2001),张力方等(2007)研究认为未来地震多发生在已发生地震的周围,笔者根据此规律建立高斯圆形模型。Gauss函数在一定程度上反映地震的空间不均匀性,又比较符合地震发生的随机性和震中定位误差的不确定性,一般取震中定位误差e作为圆形高斯光滑半径r。首先对研究区进行网格划分,在每个网格内统计地震个数,采用Gauss空间光滑函数对每个格点的地震年发生率nj(m0)在空间上进行光滑处理,光滑增量值标记为 (Frankel,1995)
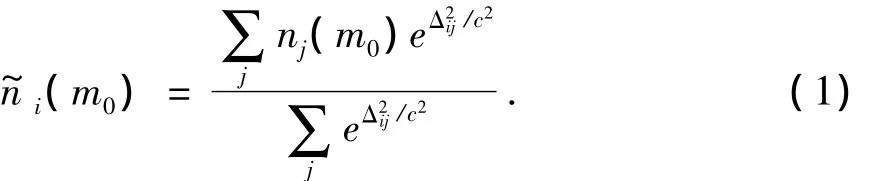
其中,Δij为第i个网格中点至第j个网格中点的距离,c为相关距离,一般取第i个网格周围3c距离内网格的数据来计算i(m0),nj(m0)是直接从地震目录统计得到网格内的地震数目。
目前我国地震资料的记录精度还不高,历史文献记录的地震资料、现代仪器记录的地震事件都存在不同的定位误差。采用高斯空间光滑函数对每个网格内的地震数目在空间上进行光滑处理,可以有效抵消这种误差。其中相关距离取决于所采用地震目录的震中定位误差,本文取r=3c≈e,e为地震目录最大定位误差。
根据光滑模型的基本假设 (Frankel,1995),经过光滑处理的地震活动率基本反映了未来中强地震 (M≥5.0)活动的格局。据我国实际情况,胥广银和金严 (1998)认为采用3.0级以上地震也基本反映这一特征,且本研究区域未来百年主要受5.0~6.0级地震的影响 (彭艳菊等,2008),所以利用现代中小震地震评价地震危险性是很有意义的。
2.2 断层导向性的椭圆空间光滑
根据Lapajne等 (2003),王健 (2001),张力方等 (2007)研究,小震活动密集区和中强震原地复发都受到其相关断裂的影响,即便是弥散性地震活动也与地震构造具有一定的关联性,地震往往优势分布于断层展布方向。虽然目前尚无法准确掌握两者的对应关系,但我们可以用一种简化模型——椭圆光滑模型,近似反应这种特征。利用回归分析得到的震级与破裂尺度之间的经验关系,统计得到地震构造单元内影响地震活动的主要断层类型及其走向等参数,确立椭圆光滑模型的相关参数。在对地震发生率的圆形光滑处理基础上,采用椭圆空间光滑函数对各网格点的地震年发生率nj(m0)进行二次光滑处理,光滑增量值标记为i(m0)(Lapajne et al,2003),可表示为该函数在一定程度上考虑了地震构造对发震的影响,又较符合地震发生的随机性。其中,R=为第i个网格到第j个网格的距离,T为转置运算符,σ为椭圆长半轴,τ为短半轴,相当于圆形光滑模型的相关距离c,椭圆的长轴方向σ为相关距离,短轴方向τ为相关距离,并且定义断层与正东方向的逆时针夹角为断层的方位角α。
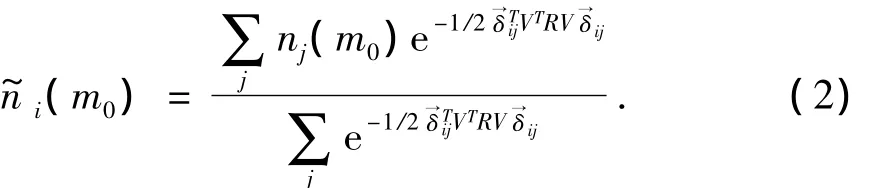
根据地震构造量化模型和华北地区震级—破裂长度关系lg(L)=a+bmu(Wells,Coppersmith,1994),可以得到椭圆模型的长半轴σ和短半轴τ与破裂长度成比例关系:σ=kL(k≥1),τ=ωL(ω<1)。这一方法明确了光滑中相关距离、平滑半径选取的物理意义,并将断层因素引进光滑函数中,使光滑后的地震空间分布更趋合理,物理意义也更加明确。根据每个网格节点所处的地震构造区,选取相应的构造模型参数 (主要断层类型、断层权重、断层走向α、椭圆σ、τ等几何参数),依据式 (2)在圆形空间光滑处理的基础上,进一步对各震级档的年发生率进行处理,最后得到起算震级的年发生率。
利用相对完整的输入地震目录,在网格内统计大于起始震级m0的地震个数nj(m0),并采用该网格所处的构造单元的椭圆光滑模型对其进行空间光滑处理得到i(m0),进而可以由其统计时段得到大于起始震级m0地震发生率i(m0)。由于在地震危险性计算中一般只考虑M≥4地震的影响,故将由不同时段、不同起始震级m0的输入目录光滑后得到的发生率i(m0)标准化4为结果,再根据双截断G-R震级分布关系得到各震级档的发生率。
2.3 震级分布关系
在本文的网格源地震危险性概率评价方法中,两个基本假设为地震事件服从泊松分布和震级指数分布,即地震事件在空间和时间上随机独立发生,我们对所涉及的地震目录删除前、余震,再进行统计分析得到地震活动性参数 (b,v等),其中地震频度 (或发生率)是概率方法重要数据。最常用的关系是G-R复发公式,是地震频度的对数与震级规模的线性关系。通常所说的单截断的G-R关系,即限定震级下限为m0,则大于m0的复发关系为

由Cornell和Vanmarcke(1969)提出双截断的地震复发关系,则m0<m<mu的复发关系为
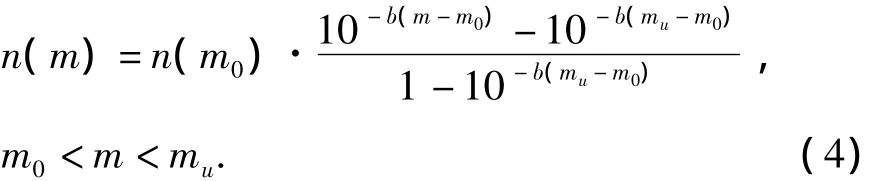
其中,n(m0)=10a-b*m0。本文采用双截断的复发关系,分别用直接统计得到m0~m0+iΔm…~mu各震级档的发生率,并求解起算震级的年发生率。
2.4 地震危险性计算
根据分段泊松分布模型和全概率公式,计算场点处地震动参数值u超过给定地震动参数值u0的年发生率为 (Reiter,1992)
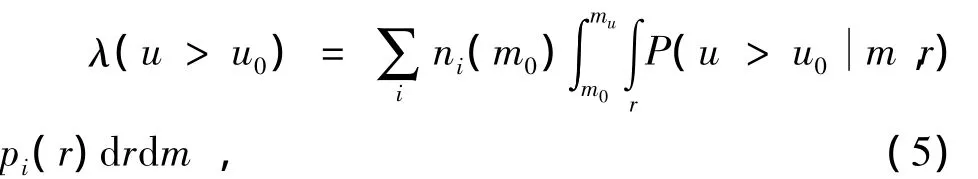

将研究区划分成 (20×20)km的网格,统计每个网格中的地震发生率,式 (5)可简写为
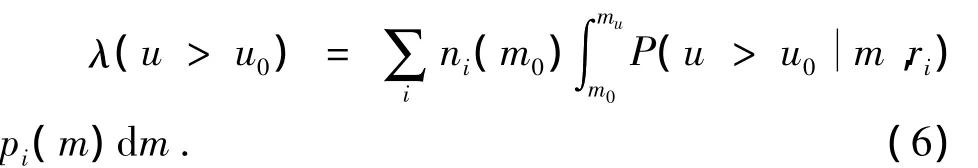
其中,ri为空间格点到计算场点的距离。基于以上点源式的概率地震危险性评价方法,得到网格节点的地震动参数。
3 东部近海海域区划研究
3.1 资料概况与完整性分析
由于地震目录作为该地震危险性分析中直接输入的重要数据之一,目录的完整性对研究结果的影响将会很大,所以我们对研究区域内地震资料的台网监测能力和定位精度进行评估。
(1)历史地震
中国东部近海海域的历史强震目录编制以《中国强地震目录》为基础,以中国地震台网中心编辑的《中国地震观测目录》为主要补充来源,并参考其他目录讨论争议地震和校核地震参数。
由于历史强震的完整性分析较为复杂,涉及到很多因素,尤其在海域地区,此处仅以M-T图做简单统计判定,认为1500年后该地区记录的M>4.7历史强震基本完整。根据《中国历史强震目录》中震中位置精度判定方法,进行了震中定位精度统计。在221次有定位精度的地震中,Ⅰ类精度有64次,Ⅱ类有46次,Ⅲ类有55次,Ⅳ类有37次,Ⅴ类有19次,74.6%的地震定位精度属于前3类,Ⅳ类和Ⅴ类定位精度地震多在海域地区,则这个研究区域的震中定位误差基本控制在90 km以内。
(2)现代地震
1970年后地震监测台网基本建设完成,对取得的仪器记录的地震目录进行完整性评价。1975、1976年海城和唐山地震的发生又推动了地震观测台网的发展,20世纪80年代地震观测台网已成体系,除东海监测能力偏低外,南北关联较好。但与目前的数字观测台网相比,关联性有很大改进(图1)各震级阈值线基本都与海岸线平行,说明各省台网的观测精度相似①中国地震局地壳应力研究所,中国地震局地质研究所.2011.地震科研行业专项研究报告——海域强震构造判断及海域工程抗震设防技术综合研究.。

图1 1980s(a)及2000~2007年 (b)沿海地区地震台网实际监控能力Fig.1 Seismic networks monitoring ability in East China offshore areas in 1980s(a)and 2000~2007(b)
根据地震活动强弱和所处位置的不同对监测能力的影响,我们把中国东部海域分为4个地区:渤海、黄渤海、南黄海和东海地区,分析不同时期和地区台网的监测震级下限。综合台网的监测能力计算结果,1970~2010年,渤海及沿岸可靠的震级下限为3.0级;黄渤海及沿岸可靠的震级下限为3.5级;南黄海及沿岸可靠的震级下限为3.5级;东海及沿岸可靠的震级下限为4.0级 (表1)。由表1可以看出,1980年以来,整个统计区内3级以上地震基本无缺失①中国地震局地壳应力研究所,中国地震局地质研究所.2011.地震科研行业专项研究报告——海域强震构造判断及海域工程抗震设防技术综合研究.。
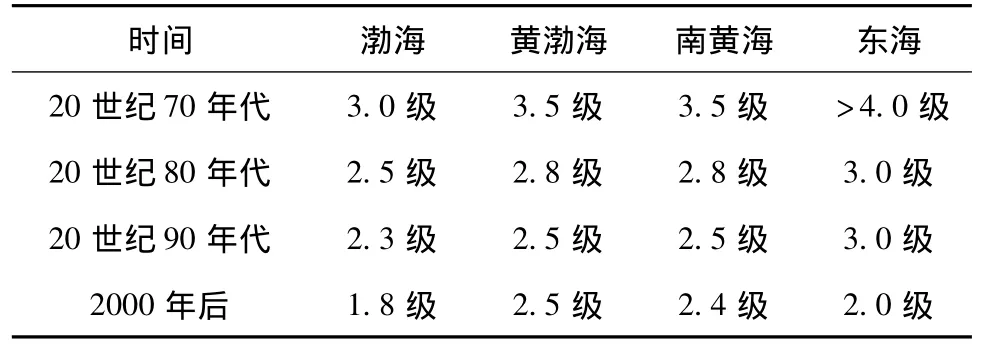
表1 不同时段、不同区域台网的监测能力估计Tab.1 Network monitoring ability estimate in different time and different regions
在1936年全球地震资料的增加和解放后我国地震基准台网的建设之后,我国东部海域地区也有了定位精度数据,随着地震观测台网不断建设,尤其是自1970年以后我国台网观测系统逐渐形成,数据在定位精度上也有了显著提高。1936~1969年无精度数据占总记录的79.1%,1970~1980年为50.5%,1980年后降到3.3%。同时I、II类精度的记录数量也逐年提高,1936~1969年I类精度均为零,II类精度为13.4%,到1970~1980年间I、II类精度占一半,1980年后I、II类精度的定位地震比例占到95%以上。
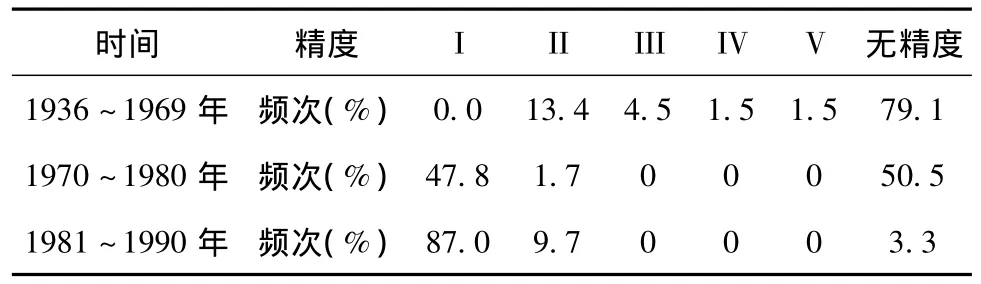
表2 各类地震定位精度比例表Tab.2 Proportion of all kinds of earthquake location accuracy
在同一时期,由于地震台网分布的特点,也会造成地震监测能力有较大差别,即地震定位精度与所处的监测区域有关,故将整个研究区域划分为不同的监测区域进行定位精度评价。以25°~30°N、30°~36°N、36°~41°N 为界,将研究区分为东海、黄海及渤海分区,进一步分析近海域地区地震定位精度问题。按精度类别分布类(“无精度”类为VI类),各分区定位精度评估得分使用公式为
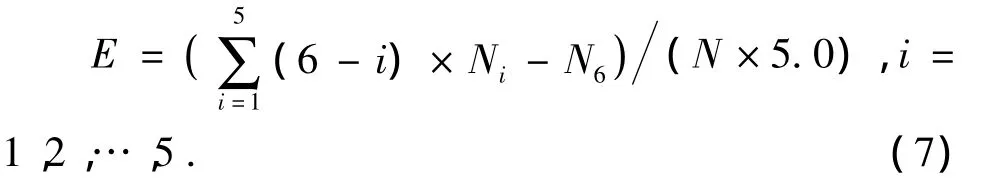
其中,E为各分区定位精度评估得分,Ni为某分区某时段的第i类精度地震的次数,N为某分区地震的总次数。
由表3可见,1935年后除东海区域仍无地震定位精度外,其它2个区有一定程度定位精度。1970~1990年地震定位精度很快提高。1990年后统计范围内已大都是I类精度。因此在危险性计算中取1980~2010年现代仪器地震目录 (源自中国地震局台网中心的地震数据库),并且通过以上统计数据可以估计1980年以来近海域地区的地震定位精度在30 km以内。
表3 各区定位精度得分评估Tab.3 Score evaluation of earthquake locationaccuracy in each regions
3.2 地震构造单元划分
我国东部近海海域的构造应力场的力源来自印度板块和太平洋板块、菲律宾海板块的共同作用 (高建理等,1992)。现代构造运动是以水平向构造应力场作用下的走滑运动为主要特征。渤海地震活动与NNE向的郯庐断裂带右旋走滑活动及与其共轭的NWW向燕渤断裂带的左旋走滑活动有关。黄海地区,特别是南黄海地区的地震活动受NE向右旋走滑断层和NW向左旋走滑的断层控制。东海地区水平差应力不强,可能与地震活动较弱有关。东南沿海近海海域的现代构造应力场以水平构造应力场作用下的走滑运动为主,地震活动受与岸线平行的滨海断裂带的控制。
在认真分析并参考前人多种构造单元划分方案的基础上,以大地构造格局及板块构造理论为主要划分依据,同时亦参考了即将颁布的第五代中国地震动参数区划图所采用的地震区带划分方案,来划分我国东部海区的地质构造单元,具体分为3个大区:环渤海构造区A、苏北—黄海构造区B、浙闽—东海构造区C,并进一步划分了8个次级统计单元,如图2所示。

图2 研究区域地震构造单元划分Fig.2 Seismotectonic unit division in study area
3.3 构造单元内活动性参数统计
各个统计区内存在明显的构造差异,这种差异很可能导致地震活动水平不同,表现为地震活动性参数 (M0,Mu,v,b)的不同,体现地震空间分布的不均一性。分别在3个海区 (A、B、C)内,依据上述地震目录的完整性分析结果,联合1500~2012年的历史地震和1980~2010年的现代仪器地震资料,利用年发生率拟合区域的b值。
龙峰等 (2006)根据华北地区发生34次4.0~8.0级地震建立以走滑为主的地震活断层的震级—震源破裂长度经验关系式为:MS=3.818+1.859lg(L),作为区域内断层的震级—破裂长度的回归关系。根据其统计数据发现,破裂宽度比破裂长度的中值为0.36,本文椭圆模型中ω值取0.36,k取1比较合理,依据此回归关系式建立断层导向的椭圆光滑模型。
每个地震构造单元内主导断层走向及其对应的权重的确定,是通过综合考虑该地区活动构造的空间展布和不同方向断层的发震能力,具体确定原则与潜在震源区方向性函数的取值原则类似,此处不再赘述。各地震构造单元中具体参数如表4中所示。
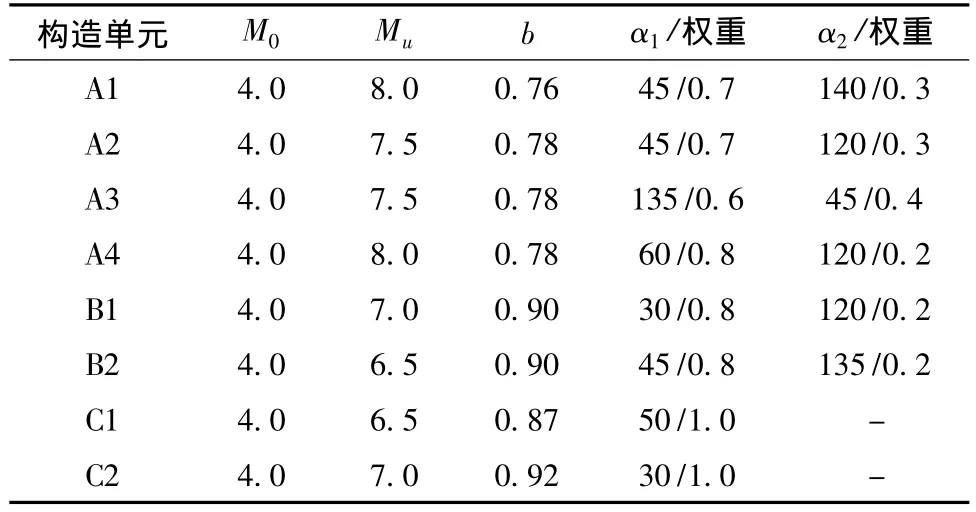
表4 地震构造单元内地震活动性参数Tab.4 Seismic activety parameter in each seismotectonic unit
3.4 建立计算模型
模型一 (M1):1500~2010年MS≥4.7的破坏性地震事件,包括历史文献记载的MS≥4■4和现代仪器记录的MS≥4.7的破坏性地震事件。根据上文分析,圆形光滑的相关距离c取30 km。
模型二 (M2):1980~2010年现代仪器记录ML>4.0的现代中小震资料,共计4 430次。圆形光滑的相关距离c取10 km。
利用以上两种地震目录和各构造单元内的构造模型参数和b值,使用二阶的空间光滑方法,可计算得到网格内的地震发生率 (或地震数目)。在本文中取网格大小为 (20×20)km,这和地震目录的定位精度相对应。进过二阶空间光滑处理得到网格点的起算震级的年发生率v~4,结果如图3所示。
为分析二阶空间光滑处理效果,笔者分别比较了未经光滑直接统计、一阶光滑和二阶光滑后得到的地震年发生率结果。在总区域内三者年发生率总和相等,即保持地震个数不变。但发生率的空间分布发生很大变化,由直接统计得到的结果发现,只在曾有地震发生过的网格内有发生率。经过考虑定位误差的圆形光滑处理结果 (即一阶光滑),年发生率数值呈高斯分布于已有地震周围,基本符合地震的原地复发特征。而经过椭圆光滑处理的结果 (即为二阶光滑)更加合理,使得地震年发生率沿主导断层走向优势分布,基本反应了区域发震构造信息,又体现了地震活动的空间不均一性。
3.5 衰减关系选取
国内外研究较多的地震动衰减关系主要针对大于6级强震动衰减模型,这样往往会低估6级以下中强地震的影响,对此高玉峰和谢康和(2000)、王海江 (2002)、金星等 (2004,2008)等进行了中小地震动衰减关系的研究,为本文中衰减关系的选取提供参考。
由于本文中所选用的地震目录都是M<7.0地震,故在加速度、反应谱、持时的回归中不再考虑地震动的近场饱和,回归模型选为:lgY=c1+c2M+c3lgR+εlgy。王海江 (2002)收集了美国西部加州地区中小地震的近场记录 (4.0≤M≤6.5,震源距R<70 km),采用回归模型,将水平方向上的两个分量各视为独立的观测值,距离取震中距,Y为峰值加速度 (cm/s2);回归结果为水平向:C1=0.467 8,C2=0.470 9,C3= -0.980 7,εlgy=0.29。金星等 (2004,2008)利用福建省地震监测台网拥有大量中小地震的速度记录,将速度记录进行仿真处理得到加速度记录,进而利用不同的模型对数据进行统计分析,得到了福建地区中小地震峰值加速度和峰值速度的衰减规律。
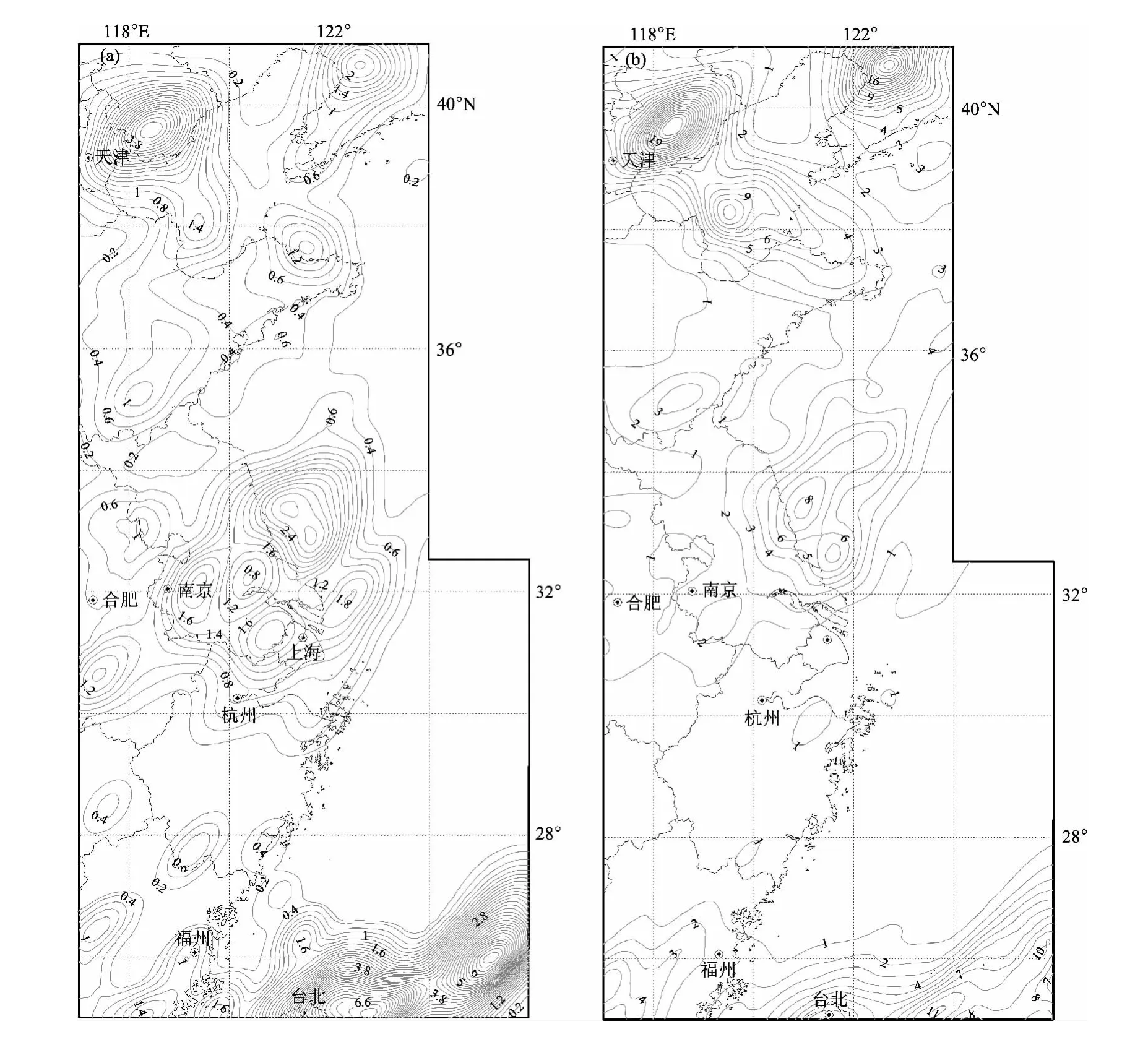
图3 由计算模型M1(a)和M2(b)经二阶光滑得到 结果分布 (单位×103)Fig.3distribution result obtained by second-order smoothing from M1(a)and M2(b)calculation Models
根据输入地震目录要与地震动衰减关系相匹配的原则,历史地震危险性评价模型 (M1)采用王海江 (2002)地震动参数衰减关系,而现代中小地震危险性评价模型 (M2)采用的金星等(2004,2008)地震动参数衰减关系。
3.6 地震危险性计算结果
基于网格源的概率地震危险性评价方法,得到4 000多个网格节点的水平向峰值加速度结果,并进行空间插值生成加速度等值线,依据表5中分档原则,编制研究区域的峰值加速度区划图。图4分别为模型M1、M2和两种模型加权的结果,结果显示峰值加速度的分布特征与该地区地震活动性分布非常一致,不同模型得到的结果反映了不同地震带来的危险性。
耕地质量统一调查研究(龚西征等) ..............................................................................................................1-36
由于不同时段、不同震级的地震目录在完整性上的差异和本身所蕴含地震信息的不同,得到的区划结果也各有不同,两者是相辅相成的。历史地震模型 (M1)结果主要反应了中强地震的影响,其优点是地震记录时间较长,基本能涵盖强震的复发周期。缺点是在某些地区地震目录漏记较严重,如在远离海岸区域,造成其危险性评估值偏低;而现代中小地震模型 (M2)结果则代表了中短期内的地震危险性,由于其地震目录的可靠性和完整性较高,使存在历史地震漏记的地区危险性得到补充,对以往低估的中等危险区有了显著提高,在江苏东部和渤中至威海海域出现两个0.2g高危险区,这是在M1结果中所没有的。但仅40多年的数字台网记录时间相对于强震的复发周期还太短,但随着观测时间的增加可能会有所改善。

表5 地震动峰值加速度分档值Tab.5 Ground motion peak acceleration value in grades
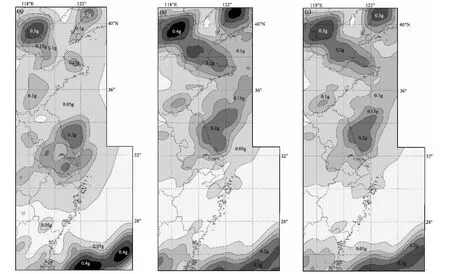
图4 50年超越概率10%的地表峰值加速度分布 (单位1g=9.81m/s2)(a)M1;(b)M2;(c)加权综合结果Fig.4 Distribution of ground peak acceleration with 10%probability of exceedance in 50 years(unit:1g=9.81m/s2)(a)Model 1;(b)Model 2;(c)weighted comprehensive results
图4c中,加权结果体现了该地区综合的地震危险性,在进行综合危险性评估时,则根据每个模型中地震资料选取时间段的不同和资料可靠性的差异,对两种模型进行了适当的加权平均,即综合模型MT=0.4M1+0.6M2。关于综合模型中的权重分配,是一个比较复杂的问题,需要建立在对发震构造的活动特征、活动强度、历史地震和古地震等进行全面了解和分析的基础上,目前的取值有待商榷,以后进一步详细分析研究。
4 结果与讨论
地震活动性参数的圆形光滑处理在地震数目不变的情况下,有效地抵消地震定位误差,而断层导向性的椭圆光滑处理方法,反应了区域构造对地震分布的影响,又体现地震活动的空间非均一性。
采用点源地震危险性概率评价方法,给出该区域50年超越概率10%的水平加速度危险性结果,特点是简单快捷,只要掌握区域大致的构造格局和相对完整的地震目录,即可以进行区域内地震危险性评估。尤其适用于像我国东部海域这样的地震构造信息尚不清楚、地震活动具有弥散性的地区。
由于不同时段、不同震级的地震目录在完整性上的差异和本身所蕴含地震信息的不同,充分利用历史强震和现代仪器记录地震,建立两个地震活动性计算模型,从而更加准确地反映该地区的地震活动,并用多种模型的加权结果确定地震危险性结果,抵消一定的系统不确定性。关于综合模型中的权重分配,需要建立在对发震构造的活动特征、活动强度、历史地震和古地震等进行全面了解和分析的基础上。地震活动性参数的空间光滑处理和逻辑树的多模型叠加方法是对我们地震危险性评价工作中关键性技术问题的新方法的积极探索和尝试。
高建理,丁健民,梁国平,等.1992.中国海区及其领域的原地应力状态[J].地震学报,14(1):17 -28.
高孟潭,卢寿德.2006.关于下一代地震区划图编制原则与关键技术的初步探讨[J].震灾防御技术,1(1):1-6.
高玉峰,谢康和.2000.中强地震区地震烈度和峰值加速度的衰减规律[J].浙江大学学报,34(4):404-408.
胡聿贤.1999.地震安全性评价技术教程[M].北京:地震出版社.
金星,康兰池.2008.福建地区中小地震地震动峰值衰减规律研究[J].地震学报,30(3):279 -291.
金星,马强,李山有.2004.利用数字强震仪记录实时仿真地动速度[J].地震学报工程与工程震动,24(1):49-84.
刘光鼎.2007.中国海地球物理场与油气资源[J].地球物理学进展,22(4):1 229-1 237.
龙峰,闻学泽,徐锡伟.2006.华北地区地震或断层的震级—破裂长度、破裂面积的经验关系[J].地震地质,28(4):511-535.
彭艳菊,孟小红,吕悦军,等.2008.我国近海地震活动特征及其与地球物理场的关系[J].地球物理学进展,23(5):1 377-1 388.
汪素云,时振梁,环文林.1990.中国近海地震活动特征[J].海洋学报,12(2):194-199.
王海江.2002.中小地震地震动衰减关系的研究[D].北京:中国地震局地球物理研究所.
王健.2001.地震活动性图象处理的网格点密集值计算方法[J].地震学报,23(3):262-267.
胥广银,金严.1998.弱震和中等强度地震活动区地震活动性模型研究//中国地震区划,学术讨论会论文集[C].北京:地震出版社.
杨勇,史保平,孙亮.2008.基于华北区域地震活动性分布的地震危险性评价模型[J].地震学报,30(2):198 -208.
张力方,吕悦军,彭艳菊,等.2008.基于中小地震应变能密度的地震活动图像分析[J].中国地震,24(4),407 -414.
张力方,吕悦军,彭艳菊.2007.用空间光滑方法评估弱地震活动区的地震活动性参数[J].震害防御技术,3(1):27-36.
Frankel.1995.Mapping seismic hazard in the central and eastern United States[J].Seismological Research Letters,66(4):8 - 21.
Lapajne J,Motnikar B S,Zupancic P.2003.Probabilistic Seismic Hazard Assessment Methodology for Distributed Seismicity[J].93(6):2 502-2 515.
Pelaez Montilla JA,Hamdache M,Lopez Casado C.2003.Seismic hazard in Northern Algeria using spatially smoothed seismicity.Results for peak ground acceleration[J].Tectonopysics,372(1 - 2):105-119.
Reiter L.1992.Earthquake Hazard Analysis:Issues and Insights[J].Surveys in Gophysics,13(3):297 -298.
Wells D L,Coppersmith K J.1994.New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J].BSSA,84(4):974 -1002.

