基于DTOA/DOA和牛顿迭代法的震源定位方法研究*

杨俊峰，张丕状

0 引言

随着现代科学技术的发展，定位技术在航空、航天、交通、震源探测、海洋勘探等领域得到了广泛地应用。定位精度的要求越来越高，在硬件系统确定条件下，可以通过改进算法提高系统的定位精度 (吕晶晶，姚金杰，2011;姚金杰，韩焱，2010)。本文提出了一种以牛顿迭代算法为基础，利用无源时差定位 (DTOA)和测量波达方向(DOA)联合定位得到微震源的估计位置的算法，本算法充分利用DTOA和DOA联合定位算法的估计特性，能够有效地解决迭代法的初始值问题，保证算法收敛并且提高迭代算法的收敛速度。通过设置建立的冗余函数表达式和结束迭代的精度范围，作为判断迭代是否结束的条件，这样既能满足一定的精度，又能提高计算速度，本文通过对计算机仿真、数据分析和计算时间来证明该算法的有效性。

1 目标定位原理

为了充分利用各种观测信息，以获取更好的定位效果，我们将观测数据中的角度信息与时间信息结合起来。本文运用的DTOA和DOA联合定位方法，主要利用主站增加对目标俯仰角的测量，形成一个包含3个子系统的冗余定位系统，各子系统分别对目标进行定位。最后对定位结果进行融合，将融合后的结果作为信源目标的初始估计值，再通过牛顿迭代算法进行精确定位。

1.1 DTOA定位原理

无源时差定位利用主站和辅站之间接收到辐射源信号的到达时间差来定位。获得时差的信息之后，通过乘以波的传播速度就可以得到信源到主站和辅站的距离差，在三维空间定位中，得到一组双曲面方程组。在三维时差定位中至少需要4个测量站才能实现对目标的定位 (陈玲，李少洪，2003)，如图1所示。

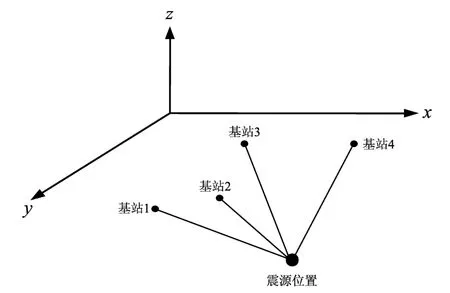
图1 三维时差定位示意图Fig.1 Schematic diagram of 3D TDOA location

设震源位置坐标为P(x，y，z)，基站坐标分别为 Pi(xi，yi，zi)(i=0，1，2，3…n)。目标到基站的距离为ri(i=0，1，2，3…n)。目标到各分站与主站(基站P0为主站)的距离差为ri0。假设有4个基站，则根据时差定位原理有以下关系

式中，t0i表示信源信号到达各分站与主站之间的时间差，c表示信号传播的速度。

1.2 DOA定位原理

测量波达方向技术在无源定位中占有极其重要的作用。随着数字信号处理技术的发展，数字相位干涉仪的测向方法由于其具有速度快、成本低、精度高的特点在工程上获得了广泛的应用。在原理上，相位干涉仪可以实现对单个脉冲测向(袁孝康，1999)。图2显示相位干涉仪 (单基线)测向原理图。

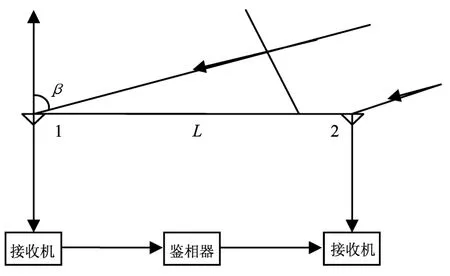
图2 单基线相位干涉仪侧向原理图Fig.2 Lateral principle graph of single-baseline phase interferometer

假设发射信号的波长为λ，与天线视线轴的夹角为β，则到达相位干涉仪两个测向天线1、2间的相位差为

式中，L为两个测向天线之间的基线长度，λ为入射信号的波长，β为入射信号与天线视线轴的夹角。由式 (2)可以得到信号的波达角为

式中，φ是两个阵元之间输出的相位差，入射信号波长的估计值λ由信号的频率估计值计算得到，基线长度L则可直接测量，在上述参数确定之后，就能根据式 (3)得到辐射源信号的入射角度β^。

2 算法

2.1 DTOA和DOA联合定位算法求初始值

利用相位干涉仪测向方法，各辅站测得的目标的俯仰角分别为

式中，αi(i=1，2，3)表示各辅站测得的俯仰角;z表示目标辐射源的高度。

将式 (1)和式 (4)组成方程组 (其中，i=1，2)，称为子系统Ⅰ，同理，将式 (1)和式(5)组成方程组 (其中，i=2，3)，称为子系统Ⅱ，式 (1)和式 (6)组成方程组 (其中，i=1，3)，称为子系统Ⅲ，这三个子系统均可完成对目标的空间三维定位，我们选择这三个子系统组成一个冗余定位系统，则该系统的定位方程组为:

其中，i=1，2，可改写为

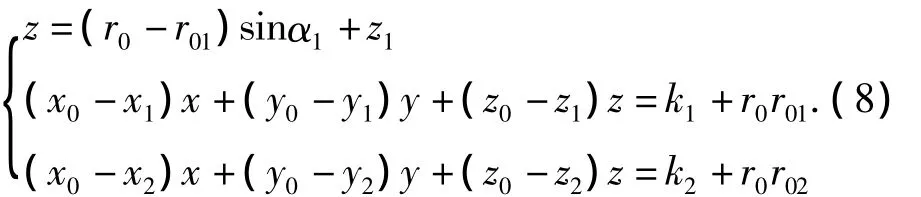
假设3个子系统所得到的目标位置分别为X^i(i=1，2，3)，定位协方差矩阵分别为Pi(i=1，2，3)，各协方差矩阵之间互不相关。SWLS融合后的目标位置为 (Petre，Li，2006;毛永毅，白菊蓉，2006)

2.2 牛顿迭代定位算法

牛顿法是一种使用导数的算法，每一步迭代方向都是沿着当前点函数值下降的方向。因此，需设定合适的初值才能保证算法是否收敛及其收敛速度。根据牛顿迭代算法的条件，将所建立目标定位模型转换为 (柳辉，2007)

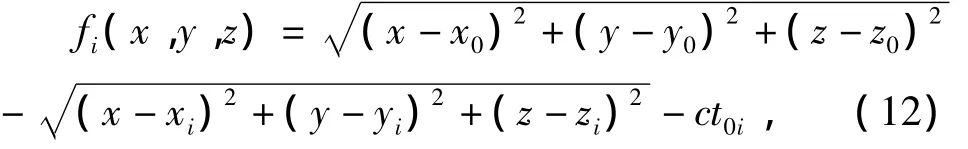
其雅克比矩阵为

当雅克比矩阵为非奇异阵，则震源坐标用牛顿迭代法表示为

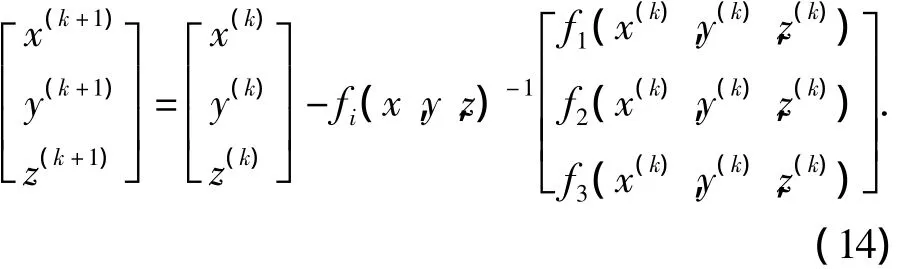
2 计算机仿真及分析

在野外条件下，通过实验完成震源定位。首先测算震动波在试验场地介质中的传播速度，再根据加速度传感器接收到的震动波数据，结合震源定位的原理及算法，得出震源的位置 (邹翔宇，徐翊峰，2010)。

震动波在该实验场地介质中的传播速度测算具体方法是:在距离待爆炸位置3 m、5 m、7 m、10 m、15 m的直线上分别依次布设5个加速度传感器A、B、C、D、E，埋深均为0.5 m，在同一位置爆炸3次，通过数据采集仪采集震动波数据，并将数据储存在计算机里，利用MATLAB对信号进行分析处理，计算出两个加速度传感器之间接收到震动信号的时间差，根据两个传感器距离震源的距离差计算震动波的传播速度v=Δd/Δt。通过计算测得的震动波传播速度如表1所示。

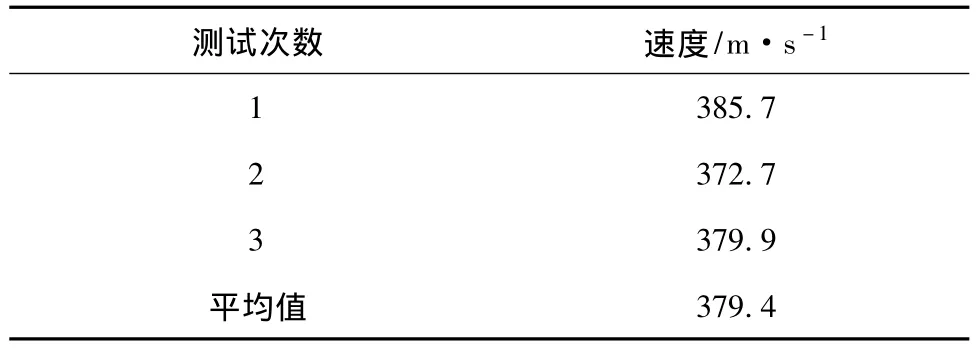
表1 震动波传播速度测算Tab.1 Measurement of vibratioon wave propagation velocity

通过加速度传感器接收到的震动波分析处理可大致得到震动波的传播规律，在距震源约7 m处的震动信号衰减为弹性波。以此为依据在待测震源周围布设加速度传感器，传感器基站的位置分别为 (6，3， －0.5)，(－4，6， －0.4)，(－6，－5， －0.42)， (7， －4， －0.28)， (0，5， －0.38)。数据采集仪的采样率为10 kHz，采样时间为6.553 8 s，采用手动触发方式。在同一地点爆炸3次，通过测算的震动波传播速度，传感器基站间接收到震动波的时差及震动定位算法以解算出震源位置。加速度传感器接收到的局部放大信号如图3所示。

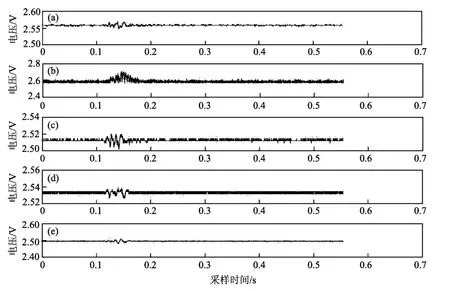
图3 局部震动信号Fig.3 Local vibration signal

表2 震源定位结果Tab.2 The source location results

利用时窗能量比法判断初至波到时，对传感器1接收到的震动信号进行预处理及时窗能量比，如图4所示。

以同样的方法判断其它各传感器接收到的初至波到时，结合各传感器基站位置及定位算法解算出的震源位置如表2所示。对运用本文算法所得定位结果进行误差分析如表3所示。

在定位过程中，由于传感器基站的布设及埋深较浅，使得Z方向的误差较大，加之震动波在传播过程中引入的误差，传感器基站站址测量误差，初至波到时估计误差等因数影响导致震源位置与实际位置之间有偏差。

从表3可知，本文算法定位结果的均方根误差值远远小于DTOA和DOA联合定位、LS-Newton法及Chan-Newton法定位结果的均方根误差值，定位结果比较理想。

图4 判断初至波时刻图Fig.4 Determine the time of the first arrival

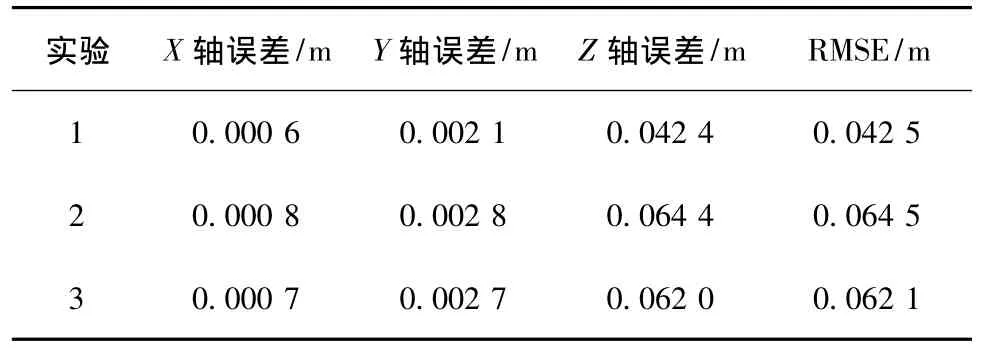
表3 定位结果误差分析Tab.3 Error analysis of positioning results

3 震源定位精度分析

通过对震源定位进行精度分析，可以了解影响定位精度的因素以及这些因素对定位精度产生的影响，因此对震源定位进行精度分析是很必要的。下文对在不同的布站形式、基站数目、初至波到达时间差估计误差、及在不同站址测量误差情况下的定位精度变化情况进行仿真分析，仿真结果可供工程参考。

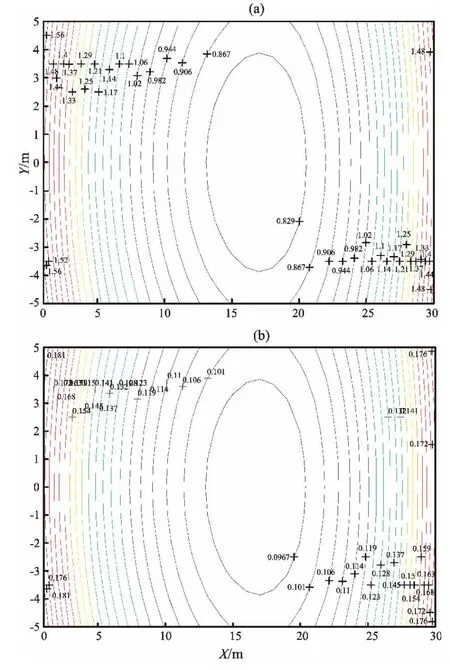
图5 不同误差情况下星型布站GDOP分布图(a)a=0.03 m，b=0.5 ms;(b)a=0.01 m，b=50 usFig.5 GDOP distribution in star-model station position under different error conditions

设震源范围是x方向0～30 m，y方向是－5～+5 m，z方向－1 m，对4个传感器基站为星型布局时进行仿真分析。图5a中存在a=0.03 m的传感器基站站址测量误差，b=0.5 ms的初至波到达时间差测量误差。图5b中存在a=0.01 m的传感器基站站址测量误差，b=50 us的初至波到达时间差测量误差。由图5b可以看出，减小传感器基站站址和初至波达到时差测量误差可有效地提高定位精度。

以4个传感器基站为例，在相同的传感器基站站址测量误差a=0.01 m和初至波达到时差测量误差b=50 us的情况下，对不同布设的定位精度进行仿真，如图6所示。从图中4种布站下的GDOP图中可知，星型布站的定位精度最高;平行四边形布站的定位次之，其在X轴方向的定位精度要高于Y轴;菱形布站和倒三角布站的定位精度较差。

图6 不同布站形式GDOP图(a)星型布站;(b)平行四边形布站;(c)菱形布站;(d)倒三角布站Fig.6 GDOP in different forms of station arrangement(a)star-model station position;(b)parallelogram-model station position;(c)dimod-model station position;(d)upside-down triangle-model station position

4 结语

本文结合DTOA和DOA联合定位法估计性好和牛顿迭代法收敛速度快的优点，提出了DTOA、DOA和牛顿迭代法相结合的地下震源定位算法。避免了DTOA和DOA联合定位法受测量误差影响较大和牛顿法对初始值选择敏感的问题。经过在野外条件下实验及仿真，实验结果表明本文算法有效地提高了震源定位的精度。在此基础上对震源系统中存在不同站址测量误差、不同初至波到达时差估计误差、不同布站形式情况下的定位精度进行了仿真分析，结果表明减小传感器基站站址测量误差和初至波达到时差测量误差可有效地提高定位精度，星型布站的定位精度要优于平行四边形布站、菱形布站和倒三角布站的定位精度。

陈玲，李少洪.2003.无源侧向测时差定位算法研究［J］．电子信息学报，(6):771－776.

柳辉.2007.解非线性方程组的牛顿迭代法及其应用［J］．重庆工学院学报，21(8):95－98.

吕晶晶，姚金杰.2011.基于最小二乘法和牛顿迭代法的空中目标定位［J］．微电子学于计算机，28(9):110－115.

吕明，郭士民.2007.基于数据融合的时差定位处理算法的应用［J］．仪器仪学报，28(4):100－102.

毛永毅，白菊蓉.2006.空间四站时差定位中的模糊及无线研究［J］．电讯技术，(6):53－57.

姚金杰，韩焱.2010.基于粒子群和牛顿迭代法的目标定位方法研究［J］．计算机应用研究，27(5):1 700 －1 713.

袁孝康.1999.相位干涉仪侧向定位研究［J］．上海航天，(3):1－7.

邹翔宇，徐翊峰.2010.基于无线传感器网络的矿震震源定位［J］．煤矿安全，(10):53－57.

Carter G C.1987.Coherence and Time Delay Estimation［J］．Proc IEEE，75(2):236－255.

Petre S，Li J.2006.Source Localization from Range-Diffrernce Measurements［J］．IEEE Signal Processing Magzine，63(11):63 － 65.