基于多目标规划的联合库存管理研究

宋雪莲

(中北大学 经济与管理学院，山西 太原 030051)

0 引 言

供应链管理是以各种技术（尤其是信息技术）为依托，在供应链各个节点间建立起战略伙伴关系，实现从原材料供应商、制造商、分销商、零售商、直到最终用户的商流、物流、信息流、资金流在整个供应链上的畅通流动，最终达到双赢甚至是多赢的过程[1]。库存管理的目的是：为了有效控制库存成本，或保证库存在满足需求的前提下，尽可能降低费用。库存成本主要有四大要素构成：1）购买成本（purchase cost）。购买所需要的原材料或半成品的费用，包括：单位购入价格或单位生产成本。2）订购成本（order cost）。向供应商发出采购订单的成本。此成本通常与订购次数有关，而与订货量无直接关系。订货成本包括：提出请购单、分析卖主、填写采购订货单、来料验收、跟踪订货、以及为完成交易所需的文职业务等项费用。3）库存持有成本（holding cost）。企业因持有库存而发生的一切费用。4）缺货成本（stock-out cost）。由于外部或内部中断供应所引起的缺货成本，包括：由于供货量不足而产生的销售利润的损失、生产损失、由于降低顾客满意度引来的损失等因素[2]。

1 库存控制的基本决策

从本质上说，库存控制的基本决策主要包括以下内容[3]：1）每次订货的间隔时间的确定(即存贮周期)；2）每次订货的订货批量的确定；3）每次订货提前期的确定；4）库存控制程度的确定，例如满足用户需求的服务水平的控制。

2 传统库存控制方法的存在问题

传统库存控制方法主要存在以下弊端：1）缺乏供应链的系统观念；2）对客户服务水平理解上的偏差；3）缺乏准确的交货状态信息；4）低效率的信息传递系统；5）忽略不确定性对库存的影响；6）缺乏合作与协调性；7）库存控制策略简单化；8）忽略了产品流程设计的影响。

3 联合库存管理的基本思想

联合管理库存(Jointly Managed Inventory，JMI)是一种供应链集成化运作的决策代理模式，在共享库存信息的基础上[4]，以消费者为中心，共同制定统一的产品生产计划与销售计划，将计划下达到各制造单元和销售单元执行。JMI 是基于协调中心的库存管理策略，强调供需双方同时参与、相互协调，共同制定库存计划，使供应链中的每个库存管理者都从相互之间的协调性考虑，在供应商和用户之间建立起合理的库存成本、运输成本、意外损失的分担机制，将VMI系统中供应商的全责转化为各个用户的部分责任，通过加强供应链管理模式下的库存控制来提高供应链的系统性和集成性，增强企业的敏捷性和响应性，体现战略供应商联盟的新型企业合作关系，是一种风险分担的库存管理模式[5]。

4 联合库存管理的运作模式

联合库存的运作模式可分为：横向联合库存和纵向联合库存[6]。1）横向联合是建立在同行业用户一体化基础上的备件共存、共享的一种库存管理模式，强调各方同时参与，共同制定库存控制计划。根据备件库存要素的不同，又可分为：虚拟联合库存、实体联合库存等形式。2）纵向联合库存可分为：原材料联合库存、产销联合库存。（1）各个供应商的零部件都直接存入核心企业的原材料库中，就是变各个供应商的分散库存为核心企业的集中库存。（2）无库存模式，即供应商和核心企业都不设立库存，核心企业实行无库存的生产方式。产销联合库存的实现形式可有多种，例如：货存供方的联合库存管理形式；货存需方的联合库存管理形式：货存第三方的联合库存管理形式；客户铺底的联合库存管理形式。

联合库存管理可有诸多运作模式，本文主要研讨产销联合库存的管理模式。关于需求的假设方面，一般情况下为了简化问题，均假设需求是确定的，但在现今人们需求多元化市场，这种假设有些不符实际；而且企业决策者考虑的目标往往不止一个，通常有多个需要同时考虑，可能会有相互冲突的目标。因此本文假设需求这为服从正态分布的随机变量，在服务水平约束条件下建立多目标联合库存控制模型[7]，针对一般的库存决策问题——(Q，r)策略中再订货点和订货量的确定，做出解释。

5 假设与符号说明

1）本文模型基于下列假设：（1）仅考虑一个生产商、一个零售商组成的局部供应链情形，且涉及产品为单一产品。供应商与生产商采用基于协调中心的联合库存管理模式，共享需求与库存信息，因此供应商可及时知道仓库的存储情况；（2）单位时间内的需求服从正态分布，且已知其均值和方差；（3）不允许缺货，决策者采用(Q，r)存储策略，即当库存水平降至，时，供应商立即运送大小为Q的货物量来补充库存；（4）提前期分固定常数和随机变量两种情形来讨论；（5）整个系统只考虑库存费、运输费、订货费(为常数，如搬运费用、联系费用等)；其中运输费分为不变费用和可变费用，可变费用假定与运输量成正比，运输成本由运输费构成，库存成本由库存费和订货费两项构成。（6）基于以上假设，可以画出库存水平随时间变化的状态图[8]，见图1。

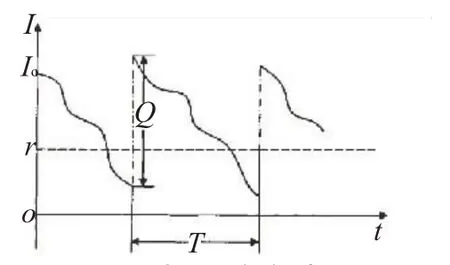
图1 时间-库存水平图

2）符号及其意义：D-单位时间内的需求:E(D)=μD, Var(X)=；DL-提前期内的需求量,在提 前 期 L 确 定 的 情 况 下 ， E(DL)=LμD,Var( DL)=；T-周期，定义为相邻两次到货的时间差；r-再订货点；V-订货提前期；Q-订货量，为了不使相邻两个周期内出现订购交叉的现象，假设Q≥r；α-在提前期内人为设定的安全水平，从概率论的角度看，口为不缺货的概率，当口接近l 时，可以认为在提前期内不会产生缺货；K-与安全水平相对应的安全因子，从概率论的角度看，k 为标准正态分布的α 分位数；β -缺货水平，定义为缺货量与供应量的比值；C0-每次订购的固定费用；C1-单位时间内的运输成本；C2-单位时间内的库存相关成本，包括订货费和货物存储费；C3-单位时间单位货物的库存成本；λ0-每次运输的不变费用；λ-单位货物的运输成本.

6 模型建立及求解方法

6.1 提前期为固定常数的情形

首先确定再订购点r：因其只跟提前期内的需求有关，由于D ∼N()，故在提前期L 内的需求DL∼服从标准正态分布。据假设，k 为标准正态分布的 α- 分位数，若令r=LμD+Κ LσD,则有：P(DL< r )=α.即提前期内需求小于再订货点的概率为α，当α 越接近1时，在提前期内就越不容易产生缺货。所以再订货点r可按下式确定：

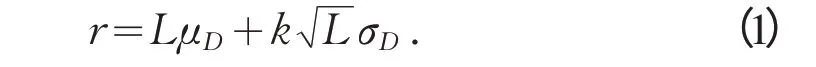
当给定α 的值后，k值可由r=LμD+kσD查标准正态分布表得到。

由于，期初库存的期望值为Q+r-LμD,期末库存的期望值为r-LμD,周期的期望值为,因此一个周期总的期望库存为Q+( r-Lμ该周期内的库存相关成本为：C=C0+C3Q+r-LμDö÷ø.由假设条件，可得一个周期内的运输成本为：C4=λ0+λQ.故单位时间内的库存相关成本和运输成本分别为：

一个周期内的期望需求量T.μD=Q,缺货量是r的函数，记为B(r) ，可由下式算得：

式中：G( k )=ϕ( k )-k[1 -Φ( k )]；ϕ( k )、Φ( k )分别是标准正态分布的密度函数和分布函数。

由于缺货水平等于缺货量与供应量的比值，则在服务水平1-β 的约束条件下，以库存成本和运输成本为目标函数的多目标规划模型为：

6.2 提前期为随机变量的情形

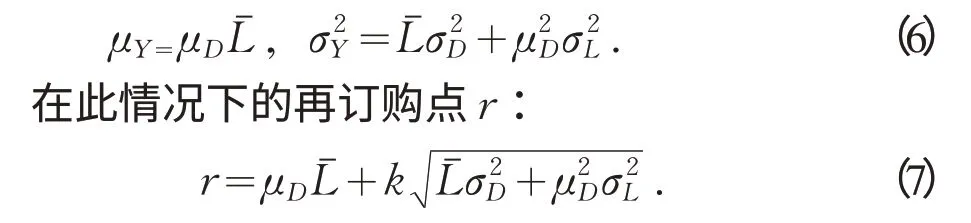
由式（7）确定的r 值，可确保k 为标准正态分布的α-分位数。当给定α 值后，可查正态分布表得到k，故由式（7）可确定再订购点的大小。而对订购量的确定，扔与提前期为固定常数情形一致。

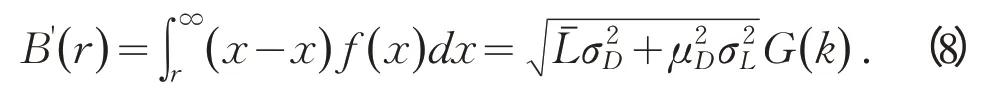
式中：G( k )=ϕ( k )-k[1 -Φ( k )]；ϕ( k )、Φ( k )分别是标准正态分布的密度函数和分布函数。

6.3 模型求解方法

本文经对目标函数各目标进行加权求和，建立了多目标规划的妥协模型：

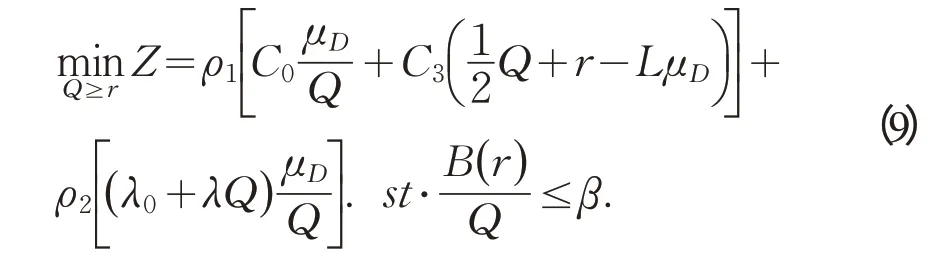
式中：ρ1和ρ2分别为C1和C2的权重值，满足：0 ≤ρ1,ρ2≤1 且ρ1+ρ2=1。

首先忽视约束条件，对Z 求一阶导数和二阶倒数：

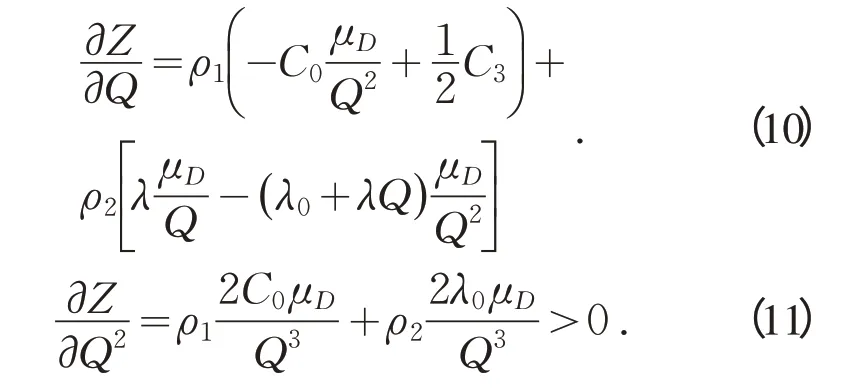
若不考虑约束条件，令式（10）等于0，可解得最优订货量为：

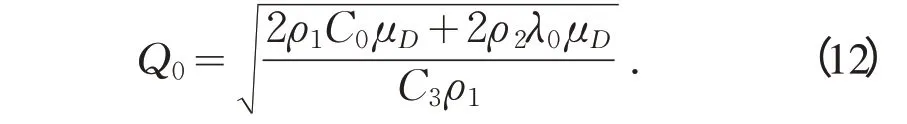
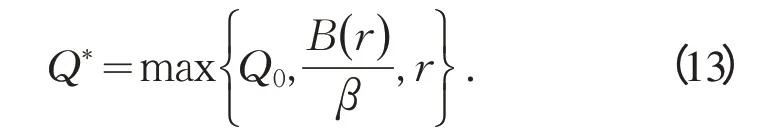
据此，订货点的确定可按不同情况采用式(1)或式(7)进行计算。

7 模型数值例题

为验证模型的有效性，取一个月时间内，令μD=600, σD=60, L=Lˉ=0.07, σL=0.1, h= 20，λ0= 100，λ=2，β=0.01，C0=250, α=0.95,查表得k=1.64，再取不同的ρ1和ρ2，对于不同的提前期类型，可得相应的r、Q 值。相应的成本，见表1。

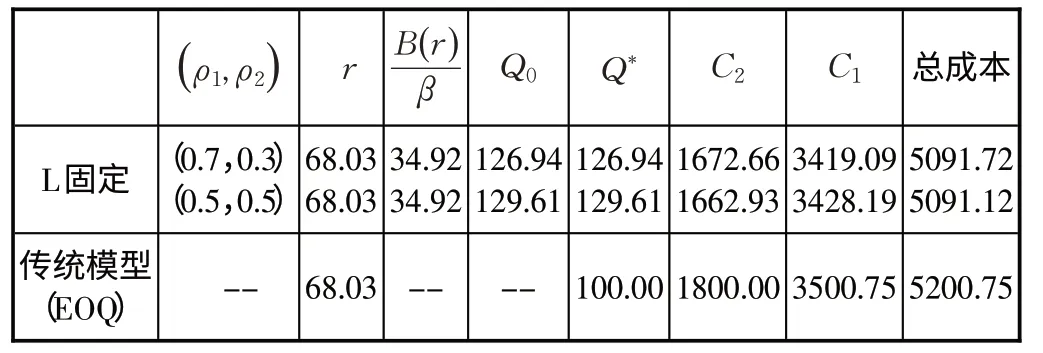
表1 提前期不同所得相应成本对照表

由表1 看出，当( ρ1,ρ2)=（0.7，0.3）时，此时决策者更偏重于对库存成本的关注，其总成本高于两者综合考虑时(即( ρ1,ρ2)=（0.5，0.5）的总成本。很显然，决策者只有综合考虑各项成本因素，才有可能使总成本降下来。再者，与传统的库存控制模型相比，这里建立的多目标模型节约了一定的成本，可说明模型的有效性。但是这个模型中还存在着一些不足，例如：具体的权系数是很难精确地确定，各企业面临的具体情况不一样，不同企业的侧重点也不同，这些都需要企业的长期经验积累，以及相互间的信任程度。这种合作模式需要企业和各级供应商之间一定的信任，否则很难达到预期效果。

[1] 柳键，马士华.供应链库存协调与优化模型研究[J].管理科学学报，2004，7(4)：11-12.

[2] 张丽锋.联合库存管理[J].软件工程师，2004（2）：60-61.

[3] 运筹学教材编写组. 运筹学[M]. 北京：清华大学出版社.2005：343-374.

[4] 达庆利，张钦，沈厚才.供应链中牛鞭效应问题研究[J].管理科学学报，2003，6(3):86-93.

[5] 徐章一，江海军.联合库存管理的四种实现形式[J].物流技术，2006(3)：28-32.

[6] MoncerHMohamed B. Some stochastic inventory models with deterministic variable lead time[J].European Jourl3al of Oper⁃ational Research，1999（113）：42-51.

[7] 侯彦斌.基于多目标规划的供应商选择模型及其实证分析[D].成都：四川大学硕士学位论文，2005：16.

[8] 马丽.基于供应链的若干随机库存模型研究[D].济南:山东师范大学硕士学位论文，2008：23.