基于集对分析的膨胀土胀缩性Vague集评价模型

魏东方，汪明武*，李 健，徐 鹏

（合肥工业大学土木与水利工程学院，合肥 230009）

膨胀土主要由亲水性黏土矿物组成，具有非饱和土的基本特性和显著的吸水膨胀、失水收缩特性[1]，且具有随时间、气候和区域变化的长期潜在危害性[2～4]，直接威胁建筑物安全。工程实践表明，对膨胀土胀缩性等级误判或漏判都可能引发工程安全事故从而造成巨大经济损失。因此，在膨胀土地区修建重要工程，准确地判定膨胀土胀缩性等级，对采取有效措施确保工程安全具有重要实际意义。

膨胀土胀缩性受诸多不确定性因素影响与控制，其评价是一个复杂的不确定系统分析问题，国内外许多学者对此问题开展研究并提出了相应的方法[5～11]。这些方法的提出使膨胀土胀缩性等级的评价由定性描述转为定量、定性全面分析，一定程度上提高了膨胀土胀缩性等级评价的准确性。但各方法都有其适用范围和局限性，膨胀土胀缩性等级评价问题至今未得到很好解决。而近期发展起来的Vague集理论在处理不确定性问题时较传统的模糊集有更强的表示能力[12]；集对分析理论则可以完整刻画确定不确定系统中的对立统一关系[13]，两者耦合可取长补短，为膨胀土胀缩性等级评价提供了新的途径。为此，本文拟提出用集对分析来构造Vague集中隶属函数的新方法，以建立膨胀土胀缩性等级的Vague集和集对分析耦合的评价模型，并结合实例验证分析模型的可行性和合理性。

1 Vague集和集对分析理论简介

Vague集理论是Gau和Buehrer于1993年提出的处理模糊问题的新理论[12]。对于论域U中任意一个元素x，Vague集A在点x的Vague值用[0,1]的子区间[tA(x),1-fA(x)]表示，tA(x)和fA(x)为隶属度的界限值，其中tA(x)为真隶属函数，表示支持“x属于A”成立的程度；fA(x)为假隶属函数，表示反对“x属于A”成立的程度。tA(x)，fA(x)∈[0,1]，并且tA(x)＋fA(x)≤1。通过tA(x)、fA(x)计算记分值，以记分值来判定待评样本符合某一等级要求的可能性。用Vague集方法来描述不确定性问题，虽然能在一定程度上克服传统模糊集方法的隶属度单一且不能反映肯定与否定状态的缺点，但是该方法不能表达介于支持和反对之间的不确定状态。

集对分析是赵克勤先生于1989年提出的处理不确定性问题的系统分析方法，在诸多领域得到广泛应用[14～18]。集对分析理论通过对事物同、异、反的分析和刻画，能全面表达确定不确定的状态，并用联系数来表达这种关系。可见，Vague集和集对分析都是解决不确定性问题的理论，若在Vague集的方法中引入集对分析，可很好解决Vague集对介于支持和反对之间的不确定状态的描述问题。

2 评价模型构建

本文基于评价样本实测值与评价标准间的同异反关系来构建Vague集隶属函数，并结合与理想类别之间的相似度及权重综合计算记分值，以判定膨胀土的胀缩等级。

2.1 胀缩性评价指标和分类标准确定

基于可操作性、广泛性和实用性原则，以及文献报导和以往成功经验，胀缩性评价选用天然含水率、液限、塑性指数、自由膨胀率、总胀缩率五个指标，以j(j=1,2,…,5)表示；胀缩性等级D={d1, d2, d3, d4}分别对应极高Ⅰ、高Ⅱ、中Ⅲ、低Ⅳ。膨胀土胀缩性等级评价指标标准值见表1。

表1 膨胀土胀缩性等级评价指标标准值Table 1 Classif i cation standard for the swelling-shrinkage grade of expansive clay

2.2 Vague集隶属度计算模型

Vague集中隶属函数的确定是其应用的关键。本文引入集对分析理论，以解决某些样本中真、假隶属度tA(x)、fA(x)可能出现负值或大于1的情况，使Vague集和集对分析耦合的评价模型具有更广的适用性。

以样本p(p=1,2,…,P)来说明，vpj表示样本p中某评价指标j的实际值，tij表示针对指标j待评样本属于等级di(i=1,…,4)的程度，不属于di的程度用fij表示。样本p中指标j的界限值为M1,j，M2,j，…，Mn,j，若样本指标属于获益型指标，则：M1,j＞M2,j＞…＞Mn,j。若vpj∈[Mi+1,j，Mi,j)则评价指标值位于该等级标准集之内，表示完全支持，即为同，相应的tij=1，fij=0；与[Mi+1,j，Mi,j)不相邻的等级标准集同vpj的关系为完全反对，即为反，此时tij=0，fij=1；与[Mi+1,j，Mi,j)相邻的等级标准集[Mi,j，Mi-1,j)、[Mi+2,j，Mi+1,j)同vpj的关系为支持、反对共存，即为异，此时隶属函数计算模型如下：

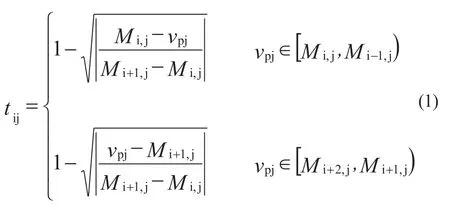
式中，Mi,j为指标j的界限值，vpj为待评样本p中指标j的实测值。

而对于损失型指标，M1,j＜M2,j＜…＜Mn,j，将区间的上下限互调即可。

2.3 胀缩性等级评价模型

任意两个Vague集之间的相似程度可用相似度表示，对Vague值分别为X=[tx，1-fx]，Y=[ty，1-fy]的两个集合，相应的X、Y的相似度Ψ(X,Y)可按下式求得：

Vague集方法以记分值来判定样本属于某一等级的可能性，即记分值越大，样本属于该等级的可能性越大。记分值的大小由记分函数求得，由于每个人对不确定性问题的认识和理解的程度不同，记分函数的确定常受主观性影响，为克服此缺陷，Vague集方法以相似度来构造记分函数。若待评样本的每个指标值都落在某一等级限定的范围内，称这样的类别为理想类别[19]。可知，对于理想类别的所有评价指标均有：t=1，f=0，Vague值为V=[1,1]。根据相似度公式(3)，以理想类别Vague值V代替X，则X=[1,1]；以待评样本p的Vague值Ap代替Y，则Y=[tij,1－fij]，考虑各指标等级判别影响程度不同，赋予其不同的权重值ωj(j=1，2，…,5)，Vague集方法定义样本p属于等级di的记分函数如下：

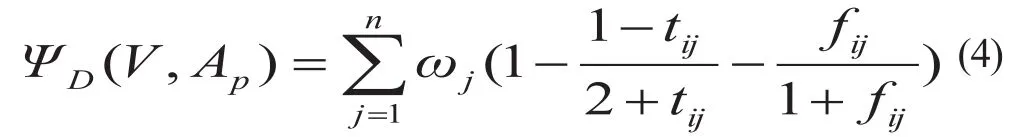
式中：V表示理想类别的Vague值；Ap为样本p的Vague值；tij、fij分别表示针对指标j待评膨胀土样本胀缩性属于等级di的真、假隶属度。ΨD(V,Ap)可简写为ΨD(Ap)。

由公式(4)计算样本p属于各个等级的记分值D(Ap)={Ψ1(Ap),Ψ2(Ap),Ψ3(Ap),Ψ4(Ap)}，基于计算的记分值，以最大记分值对应的等级作为评价结果，即Ψ1(Ap)、Ψ2(Ap)、Ψ3(Ap)、Ψ4(Ap)中最大值对应的等级即为膨胀土样本p胀缩性的等级。

3 实例应用及讨论

为验证以上模型的可行性和应用效果，现以文献[20]资料进行分析和对比。样本评价指标实测值见表2。为便于对比分析，本文各评价指标的权重直接取自文献[20]，即：ωj={0.23，0.22，0.20，0.19，0.16}，∑ωj＝1。由Vague集评价模型得到的评价结果及与其它方法判别结果的对比如表3所示。

在此以样本1中的液限指标来说明模型的计算过程。根据表1和表2可知：v11=60，M11=100，M21=55，M31=50，M41=45，M51=40，由于v11∈[55～100)，此时t11=1，t31=0，t41=0；f11=0，f31=1，f41=1。由公式(1)和(2)分别计算t21=0.667，f21=0.111；同理，可计算出样本1中其它指标的真、假隶属度。最后据公式（4）求得样本1中各指标的记分值为：Ψ1(A1)=0.800，Ψ2(A1)=0.926，Ψ3(A1)=0.104，Ψ4(A1)=0.000。可以看出Ψ2(A1)值最大，故可判断样本1的胀缩性等级为Ⅱ。同理可以求出其它样本的记分值，进而判定各样本所属胀缩性等级。

表2 评价指标实测值Table 2 Measured values of evaluation indexes

表3 样本评价结果及对比Table 3 Evaluation results of practical sample and comparison

由表3可知，用Vague集方法评价的结果与集对分析和三角模糊数方法评价所得结果完全吻合，与模糊数学以及可拓学方法所得评价结果基本吻合，此说明Vague集方法用来评价膨胀土胀缩性等级是可行的。Vague集方法的优势是能通过记分值定量表示样本属于各等级的程度，以及向其它等级转化的可能程度且判断结果准确、易于操作。如在对样本1的评价过程中，由表3可以看出，Vague集方法认为样本1与属于第Ⅱ类的理想类别的相似度为0.926，同时给出与属于第Ⅰ类的理想类别的相似程度为0.800，虽然两个值很接近，但通过比较大小仍可以看出其与第Ⅱ类的相似程度更高，故将样本1判定为第Ⅱ类。Vague集方法给出记分值的意义在于设计和施工人员可以根据记分值做多方面的准备，避免了单一评价结果的不准确可能给工程建设带来的隐患。

4 结语

膨胀土胀缩性受时间、地点、环境的影响，其等级的评价是工程界长期未解决的难题，然而却是膨胀土治理工作中首先要解决的问题。本文基于Vague集和集对分析的理论，建立了以集对分析的方法优化Vague集中的隶属函数的膨胀土胀缩性等级评价模型，并应用于工程实例分析。结果表明，基于Vague集的评价模型判断膨胀土胀缩等级是有效可行的，此为解决膨胀土胀缩等级判定和分类提供了一条新途径。但本文讨论的模型中评价指标权重采用了主观权重值，而权重的合理确定对评价结果有着重要影响，模型在实际应用中，权重合理确定尚有待深入研究和完善。

References)

[1]Wang M W, Li J, Ge S, et al. Moisture migration tests on unsaturated expansive clays in Hefei, China[J]. Applied Clay Science,2013,79:30-35.

[2]郑少河,姚海林,葛修润. 气候影响下膨胀土开裂的力学分析[J].上海地质,2007,28(2):29-32.

Zheng S H, Yao H L, Ge X R. Mechanical analysis on cracking behavior of expansive soil due to climatic condition[J]. Shanghai Geology,2007,28(2):29-32.

[3]顾中华,高广运,崔可锐. 合徐南段膨胀土分布及性质差异与地质构造的关系[J]. 上海地质,2003,24(2):15-17.

Gu Z H, Gao G Y, Cui K R. The discussion on the relationship among the distribution the quality difference of expansive soil of Hefei-Xuzhou expressway and the geological structure[J].Shanghai Geology,2003,24(2):15-17.

[4]崔可锐,周阳,管政亭,等. 合肥新桥国际机场膨胀土工程性质的试验研究[J]. 上海地质,2010,31(S1):60-63.

Cui K R, Zhou Y, Guan Z T, et al. Testing research on engineering property of expansive soil in Hefei Xinqiao Ιnternational Airport[J].Shanghai Geology,2010,31(S1):60-63.

[5]余颂,陈善雄,余飞,等. 膨胀土判别与分类的Fisher判别分析方法[J]. 岩土力学,2007,28(3):499-504.

Yu S, Chen S X, Yu F, et al. Fisher’s discriminate analysis method for identif i cation and classif i cation of expansive soil[J]. Rock and Soil Mechanics,2007,28(3):499-504.

[6]宫凤强,李夕兵. 膨胀土胀缩等级分类中的距离判别分析法[J].岩土工程学报,2007,29(3):463-466.

Gong F Q, Li X B. Distance discriminant analysis to the classification of the grade of shrink and expansion for the expansive soils[J]. Chinese Journal of Geotechnical Engineering,2007,29(3):463-466.

[7]吕海波,赵艳林,孔令伟,等. 自适应模糊神经网络在膨胀土胀缩等级分类中的应用[J]. 岩土力学,2006,27(6):908-912.

Lv H B, Zhao Y L, Kong L W, et al. Application of adaptivenetwork-based fuzzy inference systems to classif i cation of swellingshrinkage grade of expansive soils[J]. Rock and Soil Mechanics,2006,27(6):908-912.

[8]师旭超,郭志涛. 膨胀土等级判别的遗传支持向量机多分类方法[J]. 土木建筑与环境工程,2009,31(4):44-48.

Shi X C, Guo Z T. Multi-classification method of GA-SVM on identifying grade of expansive soils[J]. Journal of Civil,Architectural & Environmental Engineering,2009,31(4):44-48.

[9]汪明武,金菊良,李丽. 可拓学在膨胀土胀缩等级评判中的应用[J]. 岩土工程学报,2003,25(6):754-757.

Wang M W, Jin J L, Li L. Application of extension method to the evaluation of the grade of shrinkage and expansion for the expansive soil[J]. Chinese Journal of Geotechnical Engineering,2003,25(6):754-757.

[10]高卫东,刘永建. 熵权可拓模型在膨胀土胀缩等级判别中的应用[J]. 长江科学院院报,2012,29(11):91-94.

Gao W D, Liu Y J. Application of extenics model based on entropy weight to the classification of expansive soil’s swellshrink grades[J]. Journal of Yangtze River Scientific Research Institute,2012,29(11):91-94.

[11]Wang M W, Chen G Y. A novel coupling model for risk analysis of swell and shrinkage of expansive soils[J]. Computers &Mathematics with Applications,2011,62(7):2854-2861.

[12]Gau W L, Buehrer D J. Vague sets[J]. IEEE Transactions on Systems, Man and Cybernetics,1993,23(2):610-614.

[13]赵克勤. 集对论——一种新的不确定性理论方法与应用[J]. 系统工程,1996,(1):18-23,72.

Zhao K Q. The set pair theory[J]. Systems Engineering,1996,(1):18-23,72.

[14]赵克勤. 集对分析及其初步应用[J]. 大自然探索,1994,13(1):67-71.

Zhao K Q. Set pair analysis and its preliminary application[J].Exploration of Nature,1994,13(1):67-71.

[15]赵克勤. 基于集对分析的不确定性多属性决策模型与算法[J]. 智能系统学报,2010,(1):41-50.

Zhao K Q. Decision making algorithm based on set pair analysis for use when facing multiple uncertain attributes[J]. CAAI Transactions on Intelligent Systems,2010,(1):41-50.

[16]汪明武,李健,徐鹏. 基于粗糙集对势的优势断裂评价模型[J]. 地质论评,2013,59(4):796-800.

Wang M W, Li J, Xu P. A coupling model of rough set and set pair potential for evaluation of preferred fault.[J]. Geological Review,2013,59(4):796-800.

[17]葛松,汪明武,李健,等. 基于多属性广义集对联系度的边坡治理方案优选模型[J]. 上海国土资源,2012,33(4):64-67.

Ge S, Wang M W, Li J, et al. Optimization of slope treatment plans using a generalized multi-attribute set pair connection degree approach[J]. Shanghai Land & Resources,2012,33(4):64-67.

[18]鲍海君,曾蓉,王犁苑. 基于SPA的征地区片划分和区片交界补偿价修正[J]. 上海国土资源,2011,32(3):63-66,76.

Bao H J, Zeng R, Wang L Y. Region division for land requisition and compensation price adjustment between interfacing regions based on set pair analysis[J]. Shanghai Land & Resources, 2011,32(3):63-66,76.

[19]李凡,徐章艳. Vague集之间的相似度量[J]. 软件学报,2001,12(6):922-927.

Li F, Xu Z Y. Measures of similarity between vague sets[J].Journal of Software,2001,12(6):922-927.

[20]蔡奕,王宝军,施斌,等. GΙS环境下膨胀土胀缩等级的模糊数学评判[J]. 工程勘察,2002,(2):1-4.

Cai Y, Wang B J, Shi B, et al. To judge the swell and shrink grades of expansive soil under GΙS environment by fuzzy mathematics[J].Geotechnical Investigation & Surveying,2002,(2):1-4.