陀螺经纬仪定向中施加子午线收敛角的问题探讨

王庆林，王雅萍

(1.河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室，河南焦作454100;2.河南理工大学测绘与国土信息工程学院，河南焦作454100;3.中国矿业大学(北京)地球科学与测绘工程学院，北京100083)

一、引 言

在进行井巷工程和地铁隧道工程贯通测量时，测角误差引起支导线终点位置的横向误差是主要的误差来源，且测角误差的影响随着导线长度的增大而增加，若不加以控制，甚至可能超过生产限差的要求。为防止测角误差的累积影响，通常采取加测陀螺定向边的方法控制测角误差对导线终点位置误差的影响。在进行陀螺定向时，需要计算安置仪器点处的子午线收敛角，本文探讨了子午线收敛角计算对陀螺经纬仪定向精度的影响，并结合具体工程实例，给出子午线收敛角的正确计算方法。

二、子午线收敛角及其计算

子午线收敛角是指通过该点的子午线投影与过该点的纵坐标线之间的夹角，规定西偏为正，东偏为负。

由文献［1］可知，用大地坐标(B，l)计算子午线收敛角的公式为

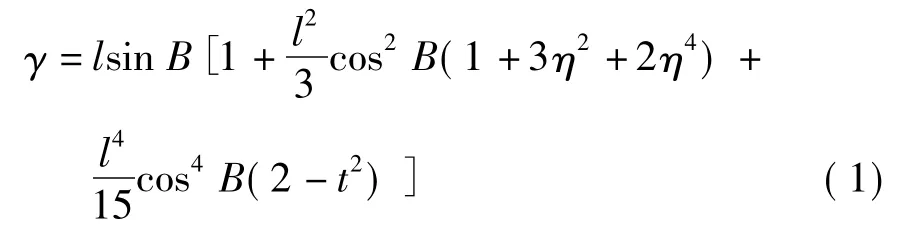
由平面坐标(x，y)计算子午线收敛角的公式为

式中，Nf为垂足点处卯酉圈曲率半径;其他有下标f者可由垂足点纬度Bf计算。

上述两个计算式计算结果以角度秒为单位，子午线收敛角计算精度为0.001″。

三、陀螺经纬仪定向计算

陀螺经纬仪定向的程序是：先在已知边上测定仪器常数Δ;再到待定向边上测定待定边的陀螺方位角;最后再次测定仪器常数。仪器常数Δ、坐标方位角α、大地方位角A和子午线收敛角γ等之间的关系如图1和图2所示。

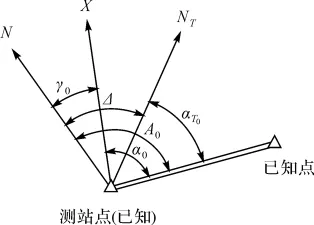
图1 陀螺仪器常数测定示意图

图2 定向边坐标方位角测定示意图

由文献［2］和图1、图2可知，仪器常数计算公式为

式中，A0为已知边的地理方位角，且A0=α0+γ0;α0为已知边的坐标方位角;γ0为测站点处子午线收敛角;αT0为已知边的陀螺方位角。

定向边的坐标方位角计算公式为

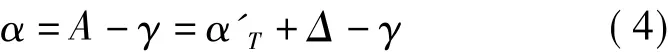
式中，A为待定边的地理方位角;γ为待定边的测站点上子午线收敛角;α'T为待定边的陀螺方位角。

将式(3)代入式(4)，经整理后得

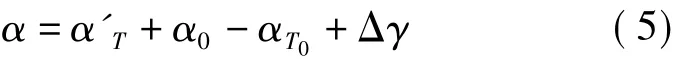
式中，Δγ=γ0－γ，为已知点和待测点处子午线收敛角的差值。

由式(5)可知，当Δγ≈0时可不考虑γ的计算。

四、不同区域Δγ的计算及分析

当测定仪器常数仪器安置点与待定向边仪器安置点相距较近时，两处子午线收敛角相差较小，可不考虑子午线收敛角的影响。那么，在用陀螺经纬仪定向时，两个仪器安置点之间相距多远时可不考虑子午线收敛角的影响，即Δγ=γ0－γ的值不至于影响定向结果的精度。下面以3°带的中纬度地区子午线收敛角计算为例讨论其对陀螺经纬仪定向结果的影响。计算区域选择：纵坐标x为3320～6650 km，横坐标y为0～115 km，沿纵坐标x按间隔1000 m、500 m、200 m、100 m，横坐标 y间隔 200 m、100 m取一点。部分计算结果整理见表1～表6。

表1 沿坐标轴Δx=1000 m、Δy=0 m，Δγ的最大变化值(″)

表2 沿坐标轴Δx=500 m、Δy=0 m，Δγ的最大变化值(″)

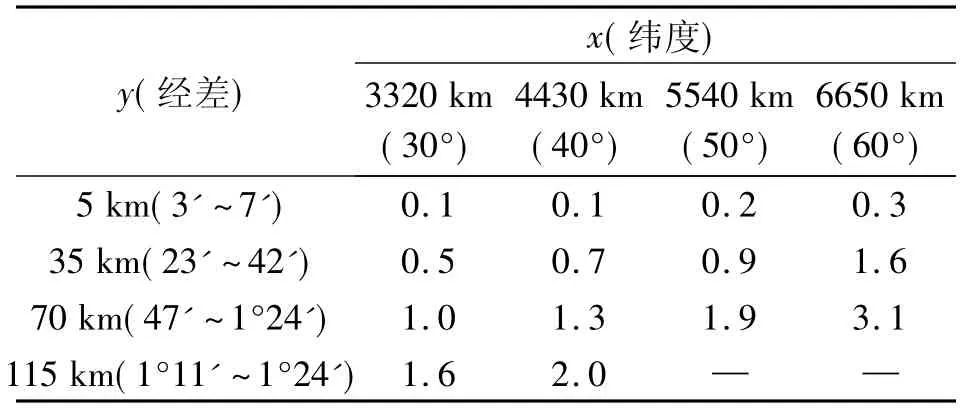
表3 沿坐标轴Δx=200 m、Δy=0 m，Δγ的最大变化值(″)

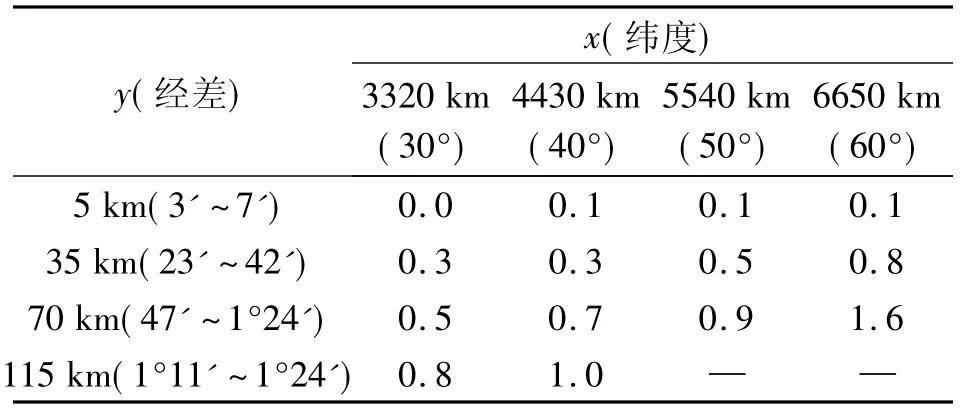
表4 沿坐标轴Δx=100 m、Δy=0 m，Δγ的最大变化值(″)

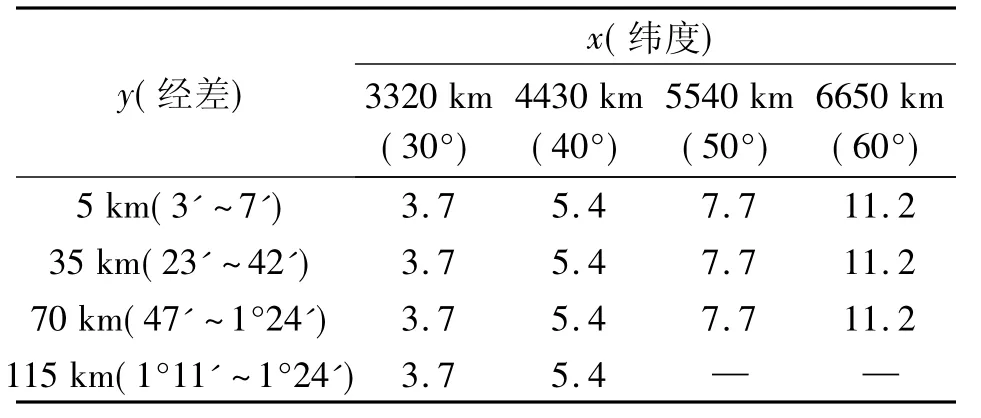
表5 沿坐标轴Δx=0 m、Δy=200 m，Δγ的最大变化值(″)

表6 沿坐标轴Δx=0 m、Δy=100 m，Δγ的最大变化值(″)

其中，表1～表4是当y坐标为定值，沿x坐标变化分别取1000 m、500 m、200 m、100 m 时两个安置仪器点之间子午线收敛角差值Δγ的最大变化值;表5和表6是当x坐标为定值，沿y坐标变化取200 m、100 m时两个安置仪器点之间子午线收敛角差值Δγ的最大变化值。

由上述计算结果可以看出，沿x轴或y轴方向相邻两点处子午线收敛角的计算差值存在如下规律：

1)当两安置仪器点的Δy=0时，子午线收敛角的差值Δγ随纬度的增大而增大，随安置点的y坐标(与中央子午线的经差)增大而增大，特别是两安置点的Δx值越大子午线收敛角的差值Δγ就越显著(由表1～表4可看出)。

2)当两安置仪器点的Δx=0时，子午线收敛角的差值Δγ随纬度的增大而增大，特别是两安置点的Δy值越大子午线收敛角的差值Δγ就越显著(由表5、表6可看出)。

3)当两安置仪器点的 y≤5 km、Δy=0、Δx≤500 m时，子午线收敛角的差值Δγ≤1″;当两安置仪器点的Δx≥1000 m时，子午线收敛角的差值Δγ随着安置仪器点的x和y坐标值的增大而增大，甚至可达到20″。

4)当两安置仪器点的Δx=0、Δy≥100 m时，子午线收敛角的差值Δγ≥1″;且Δγ随安置仪器点的x、y和Δy的增大而增大，甚至可达到20″以上。

五、Δγ对陀螺经纬仪定向的影响分析

目前所使用的陀螺经纬仪精度有25″、20″和15″，自动陀螺经纬仪的精度可达到10″以下，甚至可达3″。由上述对子午线收敛角的计算可知：

1)若不考虑两个安置仪器点所计算的子午线收敛角的差值Δγ，Δγ对陀螺定向的影响将成为系统误差，这种误差不可能从多次定向结果的精度评定中所发现。

2)当子午线收敛角的差值Δγ≤1″时，对于实际定向精度大于10″的仪器，这种计算方法造成的系统误差对定向总精度的影响不大于10%。只有在两安置仪器点的y≤5 km、Δy=0、Δx≤500 m时，可不考虑Δγ对定向结果的影响。

3)若Δγ≥1″，对于实际定向精度高于10″的仪器，这种计算方法造成的系统误差对于定向总精度将达10% 以上。特别是用于高精度的自动陀螺经纬仪定向时，这种误差甚至可超过仪器本身的定向精度，在陀螺经纬仪定向中这是绝对不允许的。

通过上述Δγ对陀螺经纬仪定向精度的影响分析，在使用陀螺经纬仪定向时，应分别计算施加两安置仪器点处的子午线收敛角γ。具体施加子午线收敛角的方法如下：

1)根据测定仪器常数安置仪器点的坐标计算子午线收敛角γ0。

2)根据待定边安置仪器点的坐标计算子午线收敛角γ。

3)根据式(5)计算定向边的坐标方位角α。如某煤矿用陀螺经纬仪定向获得的数据如下：已知边的坐标方位角 α0=277°23'04.3″;陀螺方位角 αT0=278°14'38.6″;安置仪器点的坐标为x=3 827 432.106 m，y=139 648.171 m;待定向边陀螺方位角 α'T=82°40'28.6″;安置仪器点的坐标约为x=3 827 630 m，y=139 800 m。

由式(1)分别计算两个安置仪器点处的子午线收敛角分别为

由式(5)计算得定向边的坐标方位角为

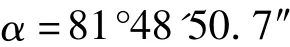
六、结束语

本文分析了施加子午线收敛角对陀螺经纬仪定向精度的影响，并用实例给出了正确施加子午线收敛角的方法，消除了过去对施加子午线收敛角的模糊认识。同时，阐明了由两个安置仪器点处的子午线收敛角的差值Δγ可造成定向结果中含有较大系统误差，这一点对于用高精度的自动陀螺仪定向尤为重要。

［1］张华海，王宝山，赵长胜，等.应用大地测量学［M］.徐州：中国矿业大学出版社，2007.

［2］张国良，朱家钰，顾和和.矿山测量学［M］.徐州：中国矿业大学出版社，2008.

［3］王庆林，陀螺经纬仪定向系统误差研究［J］.测绘科学，2010，35(5)：56-57.

［4］薛志宏，李广云，王留朋，等.陀螺定向中子午线收敛角的计算方法与精度分析［J］.测绘通报，2009(12)：43-45.

［5］邬熙娟，王维，高俊强.子午线收敛角和垂线偏差对陀螺方位角的影响［J］.南京工业大学学报：自然科学版，2007，29(3)：94-98.