基于博弈模型的共同进化降维算法在运动员营养配餐中的应用

孙俊玲

（1.武汉大学 计算机学院，湖北 武汉 430072；2.河南财政税务高等专科学校 信息工程系，河南 郑州 451464）

0 引言

作为一个特殊的人群，运动员比常人所消耗的能量物质多，需要得到更多、更全面的营养才能满足运动的需要，所以更应注意食物的合理搭配.运动员营养膳食决策模型属于一个典型的多目标优化问题.从1920年由Von Neumann建立数学基础以来，博弈理论在研究解决经济和数学领域的多目标问题方面已经有许多贡献.博弈理论引进了博弈和优化问题相关局中人的概念，在博弈理论多目标设计中，每个涉及到的局中人有他自己的目标.在博弈期间，局中人试图改进它的目标直到系统达到均衡状态.

博弈论是运筹学的一个重要分支，它所研究的典型问题是两个或两个以上的参加者（称为局中人）在某种竞争性或对抗性的场合下各自做出决策，使自己的一方尽可能得到最有利的结果.所谓博弈就是一组规则，它规定了整个博弈自始至终所应遵循的各项章程，包括局中人、策略、选定策略后的结局等等.两个局中人的策略和函数可以表示为支付矩阵，通常用一个列表来表示.如果博弈中局中人甲得到的支付值就是局中人乙失去的

进化博弈理论的主要贡献就是进化稳定战略（ESS）的概念.ESS是由著名生物学家Maynard Smith提出的，它的含义就是，进化所选择的战略，不仅执行时趋于改进的方向，而且也趋向于稳定状态.ESS是Nash均衡[1]的精华.作为替代，Maynard Smith显示，通过达尔文进化选择过程 ，可以达到博弈理论上的均衡.

1 问题描述

科学合理膳食是取得优异成绩的基础，在比赛和训练中，运动员的体力消耗很大，如果没有足够的营养补充，身体机能就会下降，影响训练效果和比赛成绩.充足的热量能够增强身体抵抗力，满足机体的需要；合理的加餐可以保证身体的健康和精力的充沛；由于其在爆发力、耐力、协调性等诸方面各有不同，不同项目的运动员有各自的需求和侧重.

1.1 运动员每日总热能供给标准

人体需要的营养主要有：蛋白质、脂肪、维生素、无机盐和水.在营养学中，能量的热量单位常采用kJ为单位来计算.

优秀运动员的每日总热能供给标准[2-3]有5级：

（1）8 372～11 721 kJ/d（均值10 046 kJ/d）.

（2）9 209～13 395 kJ/d（均值11 302 kJ/d）.

（3）11 302～17 581 kJ/d（均值14 651 kJ/d）.

（4）15 488～19 674 kJ/d（均值17 581 kJ/d）.

（5）≥19 674 kJ/d（按19 674 kJ/d）.

具体的项目划分参考表1.有减体重和控体重等要求的运动员不采用此标准.

1.2 每日三大热能营养素的供热比例

在运动员的营养膳食配餐时,食物的碳水化合物、蛋白质、脂肪的比例适当是非常重要的.其中，蛋白质营养素对于机体的修复有很大帮助；碳水化合物是运动员膳食的主要组成成分，可以有效地发挥运动员的最佳运动能力；脂肪由于在氧化时氧的利用率较低的缘故，不能满足高强度运动的需要.根据三大营养素的各自特点，优秀运动员每日三大热能营养素的供热比例标准为：

式中，Ld(s)为传递函数，T0为时间常数。根文献[9]中的评价公式，试验不同的低通滤波器的滤波效果，滤波时间常数为18时结果较为满意，所得到的滤波效果如图6所示。图中，低频部分中分配给电池承担的负载功率仍然有较高的功率需求，而此时高频部分负载功率并不大，所以在滤波器后又设计了模糊控制器来进一步处理低频部分。

脂肪提供热能的比例应该占总热能的25%～30%（游泳和冰上项目可以增加到35%）.

碳水化合物提供的热能的比例占总热能的50%～60%，其中耐力项目可以适当增加到65%或70%.

蛋白质提供热能的比例占总热能的12%～15%，其中优质蛋白不能低于30%（少年运动员可以适当增加蛋白质的摄入，以满足发育生长的需要）.

1.3 早、中、晚三餐及训练中加餐的比例分配

为了保证上、下午的训练，要合理安排一日三餐的热能供给.为保证上午的训练课的质量，运动员的早餐应该提供25%左右的热能，且各种营养素齐全和均衡.午餐热能应占35%～40%，这将有利于下午的训练课.由于运动员晚上主要是休息，晚餐的热能比例不要超过30%.训练中的加餐的总量所占的比例很小（仅占5%～10%），但对于保证训练质量也是至关重要的.

表1 优秀运动员的一日热能供给标准

2 基于博弈模型的共同进化算法

2.1 基于博弈模型的共同进化算法

每个种群相当于对局者，且种群个体的适应值作为博弈的奖赏被估算.这个奖赏来自于另一个对立种群的对局者.根据博弈模型，可以实现基于博弈模型的进化算法[4].贯穿博弈始终，每个对局者都试图最优化它们自己的目标.在进化种群中，所有个体被赋予一个适应值，适应值的大小是根据其在博弈中获胜的比率来决定.下面描述为了搜索MOP的ESS而设计的共同进化算法[5-6].

为了设计基于博弈模型的共同进化算法，需要先产生一个随机的种群.种群中每个个体都被赋予一个适应值.在博弈过程中，第1个种群的每个个体和剩余种群的其他个体进行博弈.其适应值分别由公式（1）和（2）计算.在剩余种群的其他个体依次执行同样操作.利用变异、交叉等操作，独立地产生种群的下一代个体.

下面列出了基于博弈模型的共同进化算法的步骤：

步骤1：随机产生两个种群.

步骤2：主要种群的第1个个体与另一个种群的每个个体进行博弈，计算出它的适应值.按同样方式，也可以计算出第2个种群的对应个体的适应值.

步骤4：按照第2步和第3步的处理过程，对于第2个种群的所有个体执行同样操作.

式（1）～（3）中：xi和yj分别表示第1个种群和第2个种群的个体.图1中，fa（yj）,fa（xi）,fb（yj）和fb（xi）是xi或yj分别对于fa（x），fb（x）的值.在公式（3）中，fa_max（x）和fb_max（x）指出fa（x），fb（x）对于给定变量的最大值.

步骤5：使用公式（1）和（2），确定的Fitness（xi）和Fitness（yj），计算对应的适应值，独立地产生出每个种群的下一代个体.

步骤6：终止条件不满足的话，则重复执行第2和第3步.

图1 计算收益值的目标函数

2.2 改进的基于博弈模型共同进化的降维技术（GMCE）

一个超多目标优化问题，目标集合ρ={ρ1，ρ2，ρ3，…，ρn}，决策变量集合X={x1，x2，x3，…，xk，…，xm}.假设目标对ρ1，ρ2之间存在冲突关系.超多目标优化问题ρ分为2个子问题，即问题a：ρa={ρ1，ρ3，…，ρn},Xa={x1，x2，x3，…，xm}；问题b：ρb={ρ2，ρ3，…，ρn}，Xb={x1，…，xm}.

假设2个子种群Popa和Popb，分别来表示问题a和问题b.各种群可以选择先进的多目标技术优化.通过对基于博弈模型共同进化算法的一些改进，结合常用的多目标技术可以设计求解上述问题的算法.

在种群中所有个体都被赋予一个适应值.在博弈中，第1个种群的每个个体与剩余种群的其他个体进行博弈，适应值由（1）和（2）计算.在剩余种群的其他个体用相同的方式依次执行同样操作.使用这个适应值以及交叉、变异操作，独立地来产生每个种群的下一代个体.

改进的博弈模型共同进化降维算法描述如下：

假设一个超多目标优化问题，目标集合ρ={ρ1，ρ2，ρ3，…，ρn},决策变量集合X={x1，x2，x3，…，xk，…，xm}.假设目标对ρ1，ρ2，它们之间存在完全协调关系，则根据协调关系的定义，可以删除其中的1个目标，且不会影响它的优化结果，这样可以自动达到降维的目的.如果目标对ρ1，ρ2之间互相独立，则可以转化成2个独立的n-1维的优化问题.即：子问题1的目标集合为{ρ1，ρ3，…，ρn}，决策变量集合为{x1，x2，…，xk，…，xm}和子问题2目标集合为{ρ2，ρ3，…，ρn},决策变量集合也为{x1，x2，…，xk，…，xm}；可以各自独立优化子问题1和子问题2，最后合并其各自的优化结果得到完整问题的最优解.如果ρ1，ρ2之间存在冲突关系，则可以划分多目标优化问题为2个（n-1）维子问题，即问题a：ρa={ρ1，ρ3，…，ρn},Xa=X={x1，…，xm}；问题b：ρb={ρ2，ρ3，…，ρn}，Xb=X={x1，…，xm}.它们共同进化，各自实现ρa和ρb的目标.采用改进的基于博弈模型的共同进化算法如下：

步骤1：设Popa（t）为子种群1，Popb（t）为子种群2，它们分别代表问题a和问题b；生成初始种群Popa（t），Popb（t），t=0；其中t为进化代数.

步骤2：计算种群1（即子问题a）的每个个体的目标值.但ρ1的目标值采用（4）式来计算.种群1的个体与另一个种群的每个个体进行博弈，计算反馈的奖赏值和.

对于每个个体的目标向量采用NSGA-II方法的进行分层的非支配排序，对于同层的非支配集合，计算它的支配度，按支配度来分类.这样可以得到各个个体目标向量的排序，根据排序同时结合密度估计策略计算Popb（t）每个个体的适应值.

计算它的适应值级别.第2个种群的对立个体的适应值按同样方式依次被计算.

步骤3：对于第2个种群的所有个体按照第2步类似方法执行.

计算种群2（即子问题b）的每个个体的目标值.但子问题b的ρ2的目标值采用（5）式来计算.种群2的个体与另一个种群的每个个体进行博弈，计算ρ2目标反馈的奖赏值和.

采用NSGA-II算法，对每个个体的目标向量进行分层非支配排序，对于同层的非支配集合，计算它的支配度，按支配度来分类.这样可以获得个体的目标向量排序，根据排序结果结合密度估计策略计算Popa（t）中每个个体的适应值.

步骤4：对于第2个种群的所有个体同样执行第2步和第3步的处理过程.

式（4）和（5）中：xai和xbi分别表示第1个种群和第2个种群的个体，分别是种群1中个体k的ρ2目标值和种群2中个体i的ρ1目标值；ρ1amax和ρ2bmax指出对于种群1给定个体和种群2的给定个体在目标ρ2中的最大值.其他符号的含义类似.

步骤5：如果满足的算法终止条件，则转步骤7；否则转步骤6.

步骤6：对于子种群1：Popa（t）和子种群2：Popb（t），根据已经被计算出的适应值，可以分别执行选择、杂交、变异等遗传操作，最后产生出下一代种群Pop（t+l）；t=t+l，转步骤2.

步骤7：输出结果，算法终止.

3 结果与分析

使用博弈模型共同进化的降维技术来解决运动员营养配餐设计优化问题[7]，就是在给定的运动员标准的情况下，在配餐中搜索发现各类食物及其量的Pareo最优解集，寻找目标函数空间中的目标函数的Pareo最优边界．作者以乒乓球运动员作为配餐对象，其中运动员的基本情况为：性别女，年龄20岁，体重60 kg，身高160 cm，中度劳动强度.该配餐的目标确定为：能量、蛋白质、脂肪、钠.配餐方案及营养评估如表2、表3所示.

从表2和表3可以看出，将博弈模型共同进化的降维技术应用于运动员配餐系统提高了配餐求解效果，在4目标问题求解时，能够较好地满足配餐目标需求，各个目标的误差率都小于10%.配餐方案符合专家建议的饮食要求，效果理想.

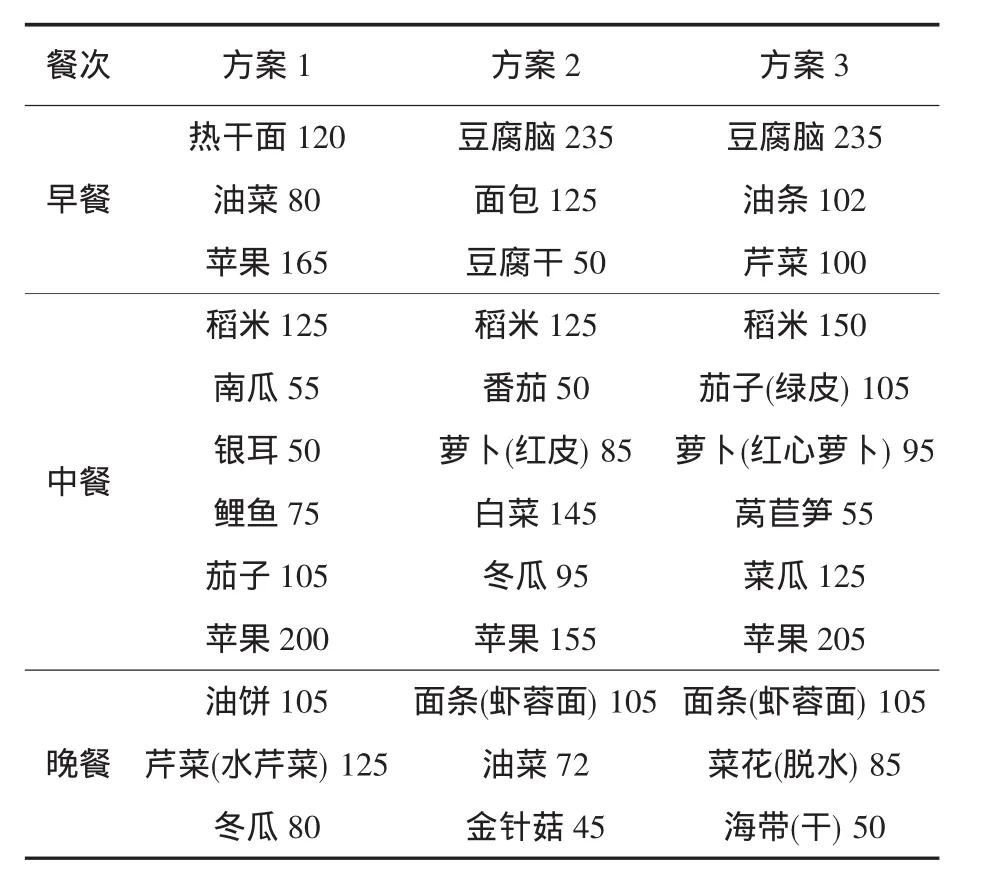
表2 乒乓球运动员配餐方案

表3 乒乓球运动员配餐方案营养评估

4 结论

对运动员营养配餐设计中的多目标优化模型进行了研究，提出了改进的博弈模型共同进化降维技术，并且应用到运动员营养配餐设计中，该方法在应用于运动员配餐中获得了较好的效果，尤其在目标多于3个的情况下，运用该算法对多个配餐方案进行了分析，优化结果验证了算法的有效性和合理性.

［1］ 陈冬.基于群智能及博弈策略的多目标优化算法研究［D］.长沙：湖南大学，2010.

［2］鲍蕾.运动员的营养膳食［EB/OL］.［2013-02-03］.http：//www.51yys.com/articles/Show Article.asp?ArticleID=89，2007.

［3］ 刘海玲.饮食营养与健康［M］.北京：化学工业出版社，2005.

［4］ 张慧.空间结构种群中基于博弈模型的合作进化的研究［D］.兰州：兰州大学，2012.

［5］ 张蕾，王高平.共同进化遗传算法在临床营养决策中的应用［J］.计算机应用，2007，27（6）：193-194.

［6］ 周盛强，向锦武.进化合作博弈在飞机总体优化中的应用［C］//第二届中国航空学会青年科技论坛文集.北京：航空工业出版社，2006.

［7］ Cui L，Wang G P.Clustering problem based on ant colony algorithm and it’s application in dietary nutrition decision supporting system.［C］//Proceedings of the 2008 IEEE Congress on ITME，USA，JEEE Computer Society Press，2008：512-515.