粮堆热学特性的数值模拟

吴才章，程明福

（河南工业大学 电气工程学院，河南 郑州 450001）

0 引言

粮食是民生的根本，是关系到社会经济稳定发展的核心物资.粮食储藏是粮食产业的核心环节，我国粮食储藏体系庞大，粮库企业数量高达2万多个，储备粮总共有1.5亿 t左右.长期以来，粮库储粮中容易出现仓房内积热多、粮堆局部发热等问题，从而导致局部乃至整体粮堆中微生物和害虫的大量繁殖，造成粮食品质劣化以及数量损耗，由此给国家造成巨大的损失.因此，对粮堆热物理学特性进行研究，进而通过非生物因素（传热、调质等方法）干预控制粮堆的温湿度变化，确保储粮安全，成为当前粮食储藏技术研究的一个热点[1-3].

对粮食热学特性的研究，国外开展得相对较早，系统地测定并研究了各种粮食的比热和导热系数及变化规律；国内相关的研究起步较晚，科研基础较薄弱[4-5]，研究主要针对粮库粮堆温度场的演化，采用宏观的研究方法，基于现场直接测量的数据，代入散粒体热学方程，通过拟合的方式获得粮堆温度场的变化，但由于缺乏对我国主要粮食品种的热物理学特性的系统研究，对粮库储藏技术的指导有限.作者从微观的角度出发，研究粮食热物理学基本参数，测定粮食的比热和导热系数，进而模拟粮库粮堆温度场的演化，为粮库通过传热、调质等方法干预控制粮堆局部发热奠定基础.同时，该课题的研究也为我国粮食湿热物理学参数测试标准的制定提供可靠的依据，为粮食储藏技术改进提供重要的理论依据.

1 粮堆导热系数测定

FD-TC-B是基于稳态法来测量不良导体的导热系数.其基本过程是，利用热源对样品加热，样品内部的温差使热量从高温向低温处传导，适当控制试验条件和参数使加热和传热的过程达到平衡状态，待测样品内部可形成稳定的温度分布，根据温度分布可以计算出导热系数[6-7].

待测样品小麦为散粒体，在试验中需要将小麦均匀的包在很薄的纤维网（网孔直径1.9 mm）中，并形成要求的形状.注意使测试样品直径与散热盘一致，而且样品厚度不应过大，否则会造成较大误差.试验中准备4组样品：豫麦49（A）、郑麦366（B）、周麦16（C）和矮抗58（D）.单次测量的试验步骤为：

（1）准备样品，测量其厚度及直径.将样品放入加热盘与散热盘中间，然后固定，调节微调螺丝使其与加热盘和散热盘接触良好.

（2）加热样品，打开电扇开关.加热盘的温度上升到设定温度值（一般设定为75～80℃）时，开始记录散热盘的温度，每隔1 min记录一次，直到加热盘和散热盘的温度在一个足够长的时间段内基本保持不变，即认为传热已经达到稳定状态，记录样品上下表面的温度分别为θ1和θ2.相关的参数测试为：环境温度为16℃；散热盘的质量m为891.4 g，比热容c为385 J/(kg·K），半径RP为65.0 mm，厚度hP为7.66 mm；样品的半径dB为65.0 mm，厚度hB为18.0 mm.4种样品A、B、C、D水分含量分别为12.1%、11.8%、11.6%、12.2%.各样品的测试结果如表1所示.

表1 样品的上下表面稳态温度

（3）取走样品后加热散热盘，使其温度在原温度基础上增加20℃左右，然后移去加热盘，开启风扇让散热盘冷却，每隔10 s记录该盘温度.作散热曲线，计算散热盘的冷却速率，散热盘的冷却曲线，如图1所示.当传热达到稳定状态时，可以认为加热盘通过样品传递的热流量与散热盘向周围环境的散热量相等，通过散热盘在稳态温度θ2时的散热速率来求热流量ΔQ/Δt.

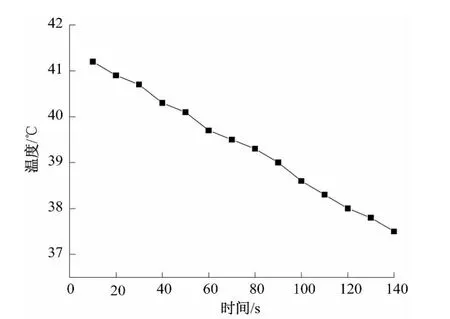
图1 散热盘冷却曲线

（4）将试验测得样品的上、下表面稳态温度θ1和θ2，热流量ΔQ/Δt以及样品和散热盘的相关参数代入导热系数计算公式，计算所测样品的导热系数λ.

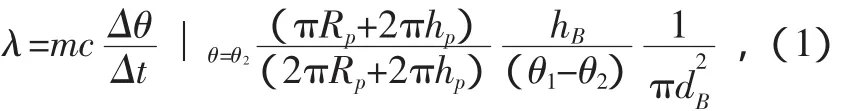
式中：λ为样品的导热系数；hB为样品的厚度，mm；dB为样品的半径，mm；m为散热盘的质量，g；c为散热盘的比热容，J/(kg·K）；Rp为散热盘的半径，mm；hp为散热盘厚度，mm.

由图1可知，豫麦49的样品下表面稳态温度θ2为38.6℃时，散热盘的冷却速率将其代入导热系数计算公式，可得豫麦49的导热系数为λA=0.161 8 J/（m·s·K）.同理，λB=0.159 5 J/（m·s·K），λC=0.159 6 J/（m·s·K），λD=0.158 3 J/（m·s·K）.

2 粮堆热学方程

2.1 粮堆的导热方程

在圆柱坐标下，根据傅里叶定理，粮堆的导热方程：

式中：ρ为粮食的密度；C为粮食的比热；λ为粮食的导热系数，J（/m·s·K）；T为粮食的温度，℃；r为柱体的半径，m；t是时间，s；φ是柱体内任意点在其截面上的角度；Z是柱体的轴向尺寸；qν为内热源.

粮堆是由有生命、非刚性、胶体颗粒组成的非均质散粒体，粮仓内粮堆的传热是一个复杂的非稳态传热过程，影响粮堆传热过程的因素较多，譬如环境的温湿度、粮食物性、粮仓的形状和结构等.为方便研究，将做适当简化，假设：

（1）粮食为各向同性的均匀介质；

（2）空气及粮食热物性参数近似不变；

（3）在初始时刻，粮堆内温度分布一致.

根据假设，在圆柱坐标下粮堆的导热方程可以简化为：

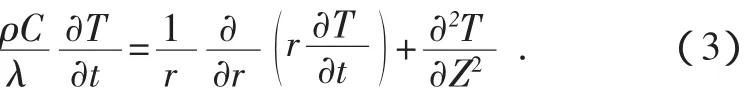
2.2 边界条件与初始条件的选取

在圆筒仓中，粮堆有3个导热边界，如图2所示.

图2 圆筒仓中粮堆的导热边界

粮堆顶部边界S1，由于粮堆与顶部空气有对流换热，它属于第三类边界条件：

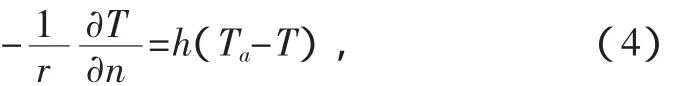
式中：h为空气和粮堆表层的对流换热系数；Ta为顶层空气的温度；T为粮堆表层的温度；n为外法线方向.

粮堆四周边界S2，由于仓壁较厚，又考虑隔热设计，它属于第一类边界条件：

式中：Tb为粮仓内壁面的温度.

粮堆底部边界S3，粮仓底部一般深入地下，一年四季保持恒温，其绝热边界条件为：

初始时刻，设粮堆整体的温度一致，即

3 粮堆温度场的数值模拟

3.1 模拟对象及参数选取

以河南省郑州市某粮食储备库中的立筒仓为研究对象，其立筒仓仓高12 m，堆粮线11 m，内径8 m，粮仓内储藏小麦，小麦品种为郑麦366.粮库所在地具有年温差较大，空气干燥等气候特点.相关的热物性参数如表2所示，郑麦366的导热系数为0.159 5 J（/m·s·K）.

表2 小麦相关的热物性参数

3.2 温度场的MATLAB模拟及求解

偏微分方程数值解方法有拉格朗日元法、有限元法、离散元法、有限差分法等.文中采用有限元法，即利用部分插值把区域连续求解的微分方程离散成解线性代数方程组，然后进行求解.对于前面粮堆非稳态导热偏微分方程，利用MATLAB的PDE工具箱进行求解，求解过程如图3所示，以图示的方式表达粮堆的温度分布.

4 结果及分析

按照求解偏微分方程的步骤，对粮堆的温度场求解需要进行几何模型设定、方程设定、初始条件和边界条件代入、网格划分及求解方程.粮仓上层空间气温设为40℃，粮仓墙壁内侧和粮堆温度均为15℃，经过求解得到粮堆的温度分布图.计算结果表明，由于粮仓墙壁具有较强的隔热效果，粮堆受四周温度影响变化不明显.粮堆顶部由于存在空气和粮堆对流换热，粮堆顶部热量交换较显著，造成粮堆上层温度自上而下呈梯度分布.1 h和10 h后粮堆顶部温度随纵深距离（Z轴）变化情况，如图4所示.

图3 利用MATLAB的PDE工具箱求解偏微分方程步骤

图4 经过1 h和10 h后粮堆顶部温度随纵深距离变化曲线

由图4可知，1 h后，粮堆温度从40℃到15℃自上而下的纵深仅为2 cm；经过10 h后，粮堆温度从40℃到15℃自上而下的纵深为12 cm，这一结论也适用于热量从四周向粮堆中间传递时温度随传递深度的变化特性.数值计算结果与粮库实测的温度场随时间变化情况一致，证明了测得的粮食热学参数值与实际是相符的.

［1］ 张忠杰，李琼，杨德勇,等．准静态仓储粮堆温度场的CFD模拟［J］．中国粮油学报，2010，25（4）：46-50．

［2］ 李灿，高彦栋，黄素逸.热传导问题MATLAB数值计算［J］．华中科技大学学报，2002，30（9）：91-93．

［3］ 贾力，方肇洪，钱兴华．高等传热学［M］．北京：高等教育出版社，2003．

［4］ 闫艳霞，曹玲芝．粮仓谷物温度场数学模型的研究与应用［J］．粮食流通技术，2007，15（4）：40-42．

［5］ Iguaz A，Arroqui C，Esnoz A，et al．Modeling and validation of heat transfer in stored rough rice without aeration［J］．Biosystems Engineering，2004，88（4）：429-439．

［6］ 张德丰.MATLAB数值分析与应用［J］．北京：国防科技出版社，2007．

［7］ 贾灿纯，曹崇文．仓储小麦温度场的数学模拟和实验研究［J］．农业机械学报，1998，29（1）：70-74.