基于混沌—支持向量机的大气污染物浓度预测模型

东北电力大学信息工程学院 付学良 杨 洋

吉林省吉林市供电公司 李纯子

1.引言

近年来，混沌理论以及非线性预测方法的发展为环境风险事件预警研究提供了新的思路。支持向量机是在统计学习理论基础上发展起来的一种新的分类和回归工具，它是针对结构风险最小化理论提出的，泛化能力强，较好地解决了高维数、小样本、非线性等实际问题，已经应用于许多领域，成功用于回归时间序列预测，分类等领域。其技术遵循结构风险最小化原则，预测性能优于神经网络。目前，大气污染物浓度预测方法多是传统统计模型，难以模拟复杂大气浓度变化。李军采用核函数为RBF神经网络对混沌序列进行预测；刘瑞平根据RBF神经网络预测混沌时间序列；罗贇赛将支持向量机理论应用于网络流量预测中，神经网络较传统模型能得到较好的预测结果，但其结构过于复杂且难于选择，收敛速度慢，容易陷入局部极值，预测精度低，且估计参数相对于较少的数据样本，导致所得到的神经网络模型相对于数据产出过拟合，即泛化能力不够。

本文仿真实验研究结果表明大气污染浓度存在混沌特性，混沌模型中相空间重构方法以及统计学习理论的支持向量机，可以将非线性序列映射到高维空间中去，此时高维空间数据便具有线性性质，并在这个空间进行线性回归。

2.混沌-支持向量机模型的建立

2.1 混沌时间序列相空间重构

研究表明一个混沌系统产生的轨迹经过一定时期变化后，最终会做一种有规律的运动。系统任一分量的演化都是由其他分量决定的，因此，可以从任一分量的时间序列中恢复原来系统的规律。Packard等建议用原始系统中的某变量延迟坐标来重构相空间，Takens证明可以找到一个合适的嵌入维m，若延时坐标的维数m≥2d+1，d是动力系统的维数，则可以从这个嵌入空间把轨迹有规律的恢复出来，这就是相空间重构理论。

根据相空间重构理论，嵌入维数d和时间延迟τ的选取至关重要，研究表明如果τ太大，会使简单轨道变得复杂且会减少有效的数据点数，τ太小，将不能展示系统的动力特征，同样d如果太小，动力系统的吸引子无法被嵌入空间包容，动力学特性无法展现；d如果太大，不仅增加计算工作量，可能会增大预测误差，而且会减少可用数据长度。

2.2 延时τ的计算方法

目前，延时τ的选择方法主要有自相关法、平均位移法、去偏复自相关法、互信息法等。本文采用序列相关法中自相关函数法大气污染浓度序列的自相关系数。

2.3 嵌入维数的计算方法

求取嵌入维数的方法主要有关联指数饱和法、假近邻法、Cao方法等，本文选用Cao方法对m进行选取。定义：

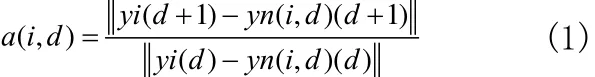
其中，E(d)是a(i,d)的平均值。

Cao发现，当d比某一个d0大时，E1(d)停止变化，于是do+1便给出了序列的最小嵌入维。同时Cao还定义E2(d)用于区分确定性混沌信号和随机信号，若随机信号E2(d)对任何d为1，对于混沌信号E2(d)将不会始终为1。

2.4 最大Lyapunov指数的计算方法

得到了延时τ和嵌入维数m以后可以计算Lyapunov指数，通过Lyapunov指数可以检验大气污染浓度的时间序列是否存在混沌现象，正的Lyapunov指数意味着混沌，即λ>0；当λ＜0，系统具有稳定不动点；当λ=0，系统具有周期性。其计算方法主要有Jacobin法、Wolf法和小数据量法。由于本文数据量小，涉及可变参数少，故采用由Sato等改进小数据量法进行计算，估计表达式为：

其中k是常数，dj( k)是基本轨道上第j对最邻近点对经过i个离散时间步长后的距离，Δt为样本周期，M为重构相空点的个数。

3.大气污染浓度预测模型的建立

3.1 混沌—支持向量机回归的空气污染浓度预测步骤

混沌—支持向量机回归预测模型主要是基于混沌和支持向量机这两个理论，根据具体的大气污染具体参数的属性，建立具体模型，具体如图1所示。

3.2 大气污染浓度预测模型的建立

对于给定的污染浓度时间序列x1,x2,…,xN-1,xN，采用相空间重构法，将其转换成维数m，延时为τ的新数据空间，即：

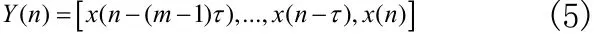
其中n∈［(m-1)τ,N］,Y( n)为重构后的相点。利用重构后的状态矢量对大气污染浓度进行预测，可以构造映射(回归估计函数)ƒ:使得：

设当前时刻为n，训练数据数量为N，则训练数据可以表示为：

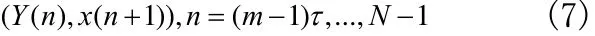
根据已知样本序列确定训练数据，应用支持向量机回归进行训练求得最佳模型ƒ；对未来时刻的预测值，以其重构相空间中前(m-1)τ变量作为输入，应用训练得到的支持向量机模型进行预报。

3.3 预测模型涉及因子及核函数的选取

(1)构建有效的预测因子。由于大气污染物浓度(y)主要受污染源的源强和气象因子的影响，故考虑将前一天的SO2浓度(x1)、净辐射量(x2)、总云量(x3)、日均湿度(x4)、日照时数(x5)、日均气压(x6)、总辐射量(x7)、平均风速(x8)、日均温度(x9)共9个因子作为预选预测因子。

(2)选择核函数及参数值。常用的核函数有线性核函数、多项式核函数、径向基函数(RBF)核函数和sigmoid核函数。

(3)用训练样本训练具有优化参数的混沌-支持向量机预测模型，获得支持向量，确定混沌-支持向量机的结构。

(4)用训练过的混沌-支持向量预测器对测试样本预测。

4.模型应用

4.1 资料来源

本文主要采用二氧化硫浓度作为仿真实验的基础数据，大气中跟二氧化硫相关参数由吉林市环境检测站提供。

4.2 实验软件

本文主要采用的开发软件是台湾大学林智仁教授等开发的Libsvm软件，此软件主要是基于MATLAB，其特点主要是简单、快捷、易于使用。是一款较好的应用与回归预测和模式识别的软件。

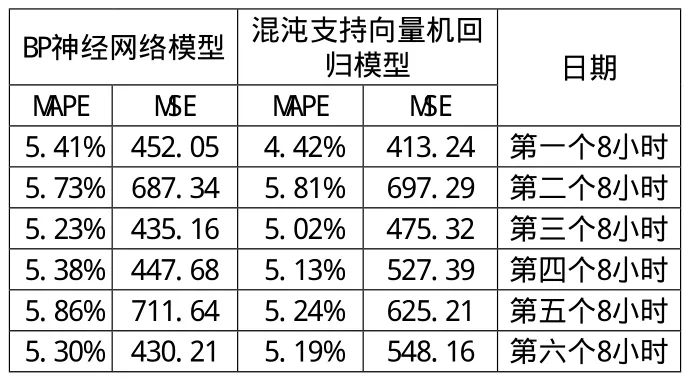
表2 两种预测模型性能比较

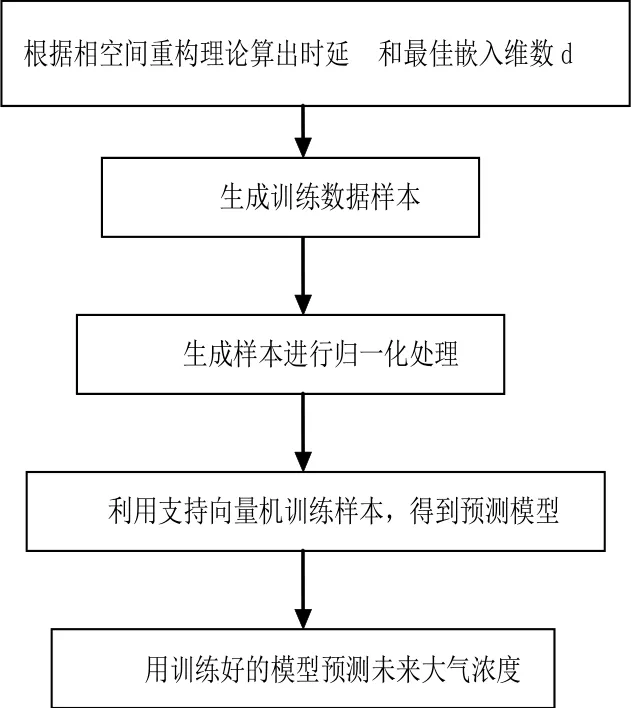
图1 混沌—支持向量机模型建立步骤

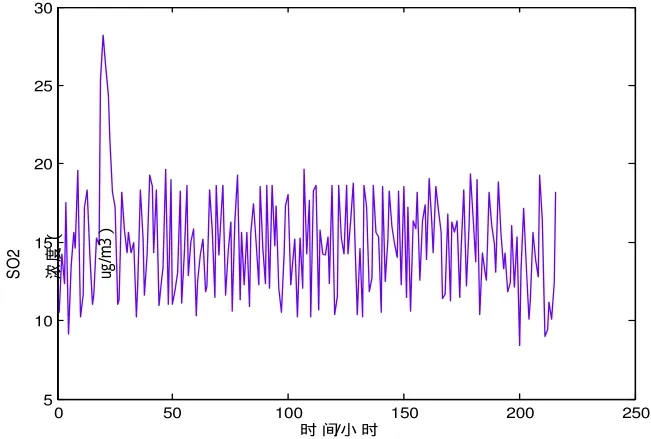
图2 采集到的原始数据

图3 7月9日、10日SO2实际值与预测值浓度对比图

4.3 仿真实验

本文采用吉林市从2011年7月1日到2011年7月10日共10天每天SO2平均浓度作为原始数据，得到10*24=240个数据；用前8天的192个数据作为已知数据来进行模型训练；后2天的48数据作为预测数据来检测模型的预测结果精确性。

采用自相关函数法得到前8天SO2，浓度序列延时为3，利用小数据量法得到Lyapunov指数为λ=0.167，利用Cao方法得到嵌入维数为10>0，说明该浓度时间序列具有混沌特性，利用相空间重构得到216个训练样本，下一步用支持向量机回归对得到样本进行训练。采集到的基础数据如图2所示。

支持向量机回归模型在训练时有较少的可调参数，即不敏感系数ε、宽度系数ζ和惩罚因子C。对以上三者取值并进行组合训练，选择误差最小一组参数为最佳，若结果不理想，重新设定以上数据进行训练。最后确定ζ=0.7ε=0.001。由交叉实验选取惩罚因子C=1000，核函数g=0.001，训练误差e=0.0001。利用训练好的模型对数据进行预测，其实际值和预测值对比效果如图3所示。

4.4 检验预测效果

目前发展最快的预测模型是神经网络回归模型，因此用支持向量机回归预测值与BP神经网络评估样本进行对比，采用平均相对误差（MAPE）和均方误差(MSE)评价SVM模型的预测性能。具体公式如下所示：

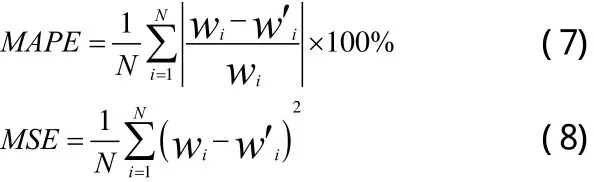
将得到的48小时数据每8小时取一次平均值，比较两个模型的预测效果。如表2所示。

5.结论

本文研究了大气污染浓度的时间序列并证明其混沌特性，利用支持向量机回归理论对大气污染浓度进行预测。根据相空间重构理论，通过相空间重构将SO2浓度序列映射到高维特征向量空间形成相点构造训练样本，解决了样本确定的问题。再根据训练样本对使用支持向量机回归理论构造预测模型，建立了混沌-支持向量机大气污染浓度预测模型，对大气污染物SO2浓度进行预测。研究结果表明混沌-支持向量机回归模型能够有效地预测大气污染浓度，与BP神经网络方法相比具有更好稳定性和预测精度，更适合于大气污染浓度预测。

[1]白鹏,张喜斌.支持向量机理论及其工程应用实例[M].西安:西安电子科技大学出版社,2008:41-55.

[2]金龙.人工神经网络技术发展及其在大气科学领域的应用[J].气象技术,2004,32(6):12-13.

[3]史志才.网络风险评估方法研究[J].计算机应用,2008,11.

[4]刘瑞平,沈福民.混沌时间序列预测与目标检测[J].雷达科学与技术,2006,3(6):327-331.

[5]罗贇赛.混沌—支持向量机回归在流量预测中的应用研究[J].计算机科学,2009,7.

[6]李目,何怡刚.混度时间序列的混合遗传神经网络预测方法[J].系统仿真学报,2008,11.

[7]梁新荣.支持向量机在混沌系统预测中的应用[J].计算机学报,2009,9.

[8]黄佳聪.智能算法及其在环境预警中的应用[J].环境监控与预警,2010,6.

[9]于国荣,夏自强.混沌时间序列支持向量机模型及其在径流预测中的应用[J].水科学进展,2008(1):117-119.

[10]吕金虎,陆军安,陈士华.混沌时间序列分析及应用[J].系统仿真学报,2002.

[11]刘杰,黄亚楼.基于BP神经网络的非线性网络流量预测[J].计算机应用,2007,27(7):1770-1772.

[12]陈俏,曹根牛.支持向量机应用于大气污染物浓度预测[J].计算机技术与发展,2010,5.