空空导弹射后动态可攻击区计算*

吴胜亮，南 英

(南京航空航天大学航天学院，南京 210094)

0 引言

在现代空战中，由于存在群体飞行器攻防对抗，为高效率的发挥空空导弹的作用，存在许多问题需要研究[1]，如以下两个问题亟需解决:

问题一:当多枚空空导弹协同拦截一群机动突防飞行器时，网络指挥作战中心通过数据融合技术对战场进行完整评价，做出战术决策，分配空空导弹，然后每枚空空导弹分别锁定各自分配的目标飞行器进行跟踪拦截。但在双方四维飞行对抗过程中，使用最初的分配方式进行拦截会被“乱套”，即被空空导弹Missile A跟踪拦截的目标飞行器在某一战斗时刻离空空导弹Missile B很近，空空导弹Missile B瞬间即可命中该目标飞行器。因此，在各个战斗时刻，如何重新分配拦截目标的各枚空空导弹?

问题二:在众多飞行器集群攻防对抗中，当两枚或两枚以上的空空导弹协同拦截同一目标飞行器时，若目标飞行器被其中的一枚空空导弹成功拦截，那么剩余的空空导弹仍然具有拦截能力。这些还具有拦截能力的剩余空空导弹该如何拦截其它目标飞行器?

事实上，以上两个问题都需要解决空空导弹发射后沿着拦截某目标的弹道飞行一段时间后，在各种限制条件下，能够命中其它哪些空域中机动飞行的目标。目前，战机(如F-16C/D)上的火控系统[2]只具备计算发射时刻的空空导弹动态可攻击区的能力。从公开发表的文献来看，国内外的学者主要从以下四个方面对空空导弹发射时刻动态可攻击区进行研究:1)空空导弹可攻击区的计算[3－6];2)空空导弹可攻击区的拟合[7－10];3)空空导弹非逃跑包络[11－12];4)空空导弹发射条件的改变对可攻击区边界的影响[13－14]。而空空导弹射后动态可攻击区的研究至今尚无文献涉及。若能进行空空导弹射后可攻击区的概念研究与飞行数值仿真计算，则对群体飞行器攻防对抗有着十分重要的使用价值，文中针对此射后可攻击区的概念问题进行了研究、分析，具体表述如下。

1 问题描述

传统概念上的空空导弹动态可攻击区的计算是以攻击机为参考，随着目标进入角的不同，计算出空空导弹能命中目标空域的远边界和近边界。对于具有全向攻击能力的空空导弹，这些点围成了一个连通的区域。对于非全向攻击发射的空空导弹，其攻击区还要受到载机和目标的机动过载限制，而形成侧边界。以示区别，文中把传统概念上的空空导弹动态可攻击区称作空空导弹发射时刻动态可攻击区。

定义 空空导弹射后动态可攻击区是指空空导弹发射后沿着拦截某目标的弹道飞行tp/s后，基于导弹的飞行状态(飞行位置矢量与速度矢量等)，发动机的工作状态，弹体质量，制导导航与控制系统等各子系统的状态，在各种约束条件下，能够以一定的概率命中目标的四维空间区域，即:

其中:Rmax|t=tp、Rmin|t=tp、Lmax|t=tp、Dmax|t=tp分别表示空空导弹发射后tp时刻可攻击区的最大可拦截边界、最小可拦截边界、左侧边界曲面和右侧边界曲面;(nmax，V，h)|t=tp分别表示tp时刻空空导弹的最大可用过载、速度和高度;(nT，VT，hT，qT)|t=tp分别表示 tp时刻目标飞行器的机动过载、速度、高度和进入角;N1，N2，…为其他约束条件，如导弹推进系统特性、气动力特性，各子系统中存在的各种随机误差与干扰;目标飞行器的机动类型;外界条件如大气风场等。

2 数学模型

2.1 空空导弹运动数学模型

导弹的6－D运动微分方程为:

式中:XT(t)=(V，θ，ψV，h，x，z，ωx，ωy，ωz，Γ，φ，φ，α，β，σ)为导弹飞行状态，其中:V、θ、ψV分别为导弹的速度、轨迹倾角和轨迹偏角;h、x、z分别为导弹所在的高度、经度方向上和纬度方向上的距离;α、β、σ分别为导弹迎角、侧滑角和滚转角;ωx、ωy、ωz分别为绕弹体 x、y、z三轴的转动角速度;Γ、φ、φ 分别为与 ωx、ωy、ωz相对应的欧拉角;控制变量 U(t)=(δx，δy，δz)即导弹气动舵偏角;导弹的系统参数 PM=(Cx，Cy，Cz，Fp，m，˙m，S)，其中 Cx、Cy、Cz分别为导弹的阻力系数、升力系数和侧力系数;Fp为发动机的推力;m为导弹的质量;˙m为导弹的质量消耗率，S为导弹的特征面积。w(t)为风场的加速度与速度;目标飞行状态XT(t)=(VT，θT，ΨVT，hT，xT，zT)参见目标数学模型;t为导弹(目标)的飞行时间。

2.2 导弹制导律数学模型

空空导弹采用三维空间的比例导引律。比例导引律下，空空导弹指令加速度为:

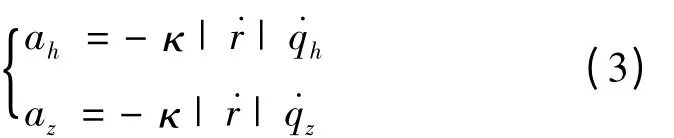
式中:ah、az分别表示俯仰加速度和偏航加速度;κ为比例系数;为目标相对导弹的距离变化率 分别表示空空导弹 －目标连线(LOS)的旋转角速度在地面坐标系y轴和z轴上的分量。

2.3 导弹的气动力模型与推进系统模型

升力系数Cy和升阻比λ随飞行马赫数Ma、攻角 α 的变化，如图1～图2所示。在发动机工作期间(10s之内)，推力大小与质量消耗率为:

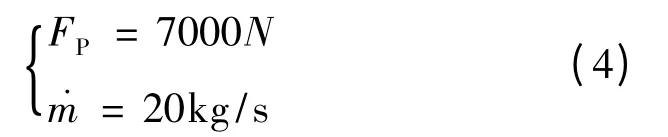
图1 Cy随 Ma、α的变化

2.4 目标运动数学模型

目标飞行运动微分方程:

式中:下标 T代表目标，(aT，aTh，aTz)为目标在笛卡尔坐标系下的机动加速度。通过设立目标飞行加速度(aTx，aTh，aTz)随 时 间变化的函数，即可产生不同类型的任意 4－D机动突防飞行轨迹(t，hT，xT，zT)。

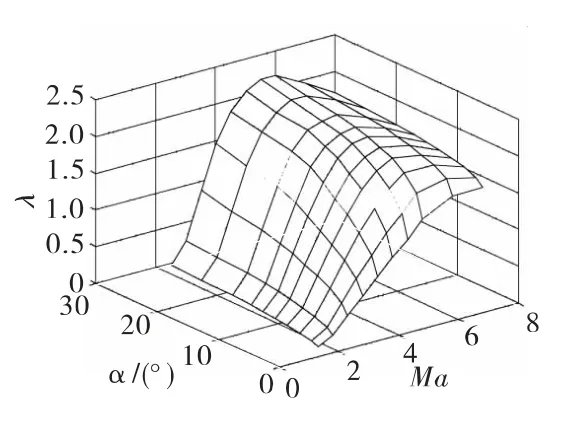
图2 λ随Ma、α的变化

3 可攻击区边界计算方法

3.1 发射时刻动态可攻击区边界计算方法

文中基于空空导弹与目标数学模型，根据载机与目标的飞行状态等因素，提出采用快速模拟算法计算传统定义的空空导弹可攻击区的最大可拦截边界。即以大于空空导弹最大拦截距离某个距离数值作为拦截距离的初始值，以空空导弹最大工作时间tmax、空空导弹相对目标的最小接近速度ΔVmin、空空导弹最大可用过载nmax以及最大视线俯仰角|Ω|max、最大视线方位角|ψ|max等作为计算可攻击区最大可拦截边界的约束条件，根据允许的脱靶量ε判断空空导弹是否击中目标飞行器。若没有击中，则以此距离减去对应的脱靶量作为下次迭代计算的初始值，如此循环计算，最后得到传统定义的空空导弹可攻击区最大可拦截边界。编写程序时，假设在铅垂面上，视线俯仰角向上为正，向下为负;在水平面上，视线方位角向左为正，向右为负。因此，需要计算视线方位角(－45°～45°)、视线俯仰角(－90°～90°)范围内的空空导弹可攻击区最大可拦截边界。这种算法与传统的二分法或黄金分割法相比，在允许的精度范围内，运算速度快，运算量小。传统定义的空空导弹可攻击区的最小可拦截边界计算与最大可拦截边界计算方法相同，但是约束条件不同。传统定义的空空导弹可攻击区最大可拦截边界的计算流程图如图3所示。

3.2 射后动态可攻击区边界计算方法

对于空空导弹射后动态可攻击区的边界，计算方法如下:基于导弹与目标模型，根据空空导弹沿着某条弹道(攻击某目标)飞行ts时间后的状态信息(导弹的速度、轨迹倾角、轨迹偏角位置发动机工作状态;迎角、侧滑角等)与目标的飞行状态等因素，采用快速模拟算法，计算出空空导弹射后动态可攻击区的远边界和近边界。

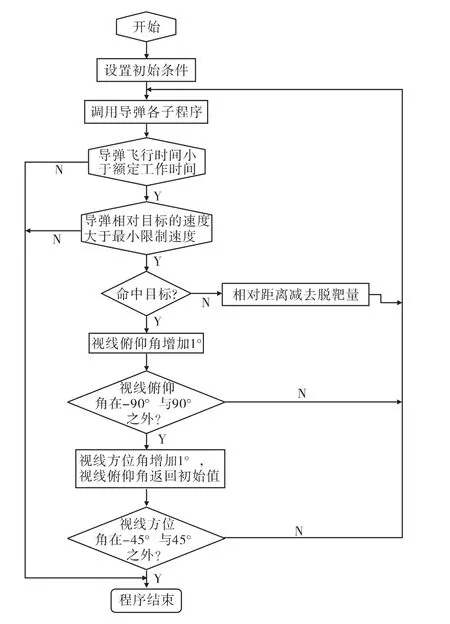
图3 可攻击区边界计算流程图

4 数值仿真与分析

4.1 3D 可攻击区

为了表述方便，文中对目标飞行器的机动类型进行定义。

Ⅰ型U机动目标飞行器:目标飞行器初始飞行方向背离导弹飞行(即初始时刻导弹尾追目标飞行器)，目标飞行器作U型机动飞行之后，朝向导弹飞行(即目标飞行器作U型机动后，导弹迎击目标飞行器)。

Ⅱ型U机动目标飞行器:目标飞行器初始飞行方向朝向导弹飞行(即初始飞行时刻导弹迎击目标飞行器)，目标作U型机动飞行之后，背离导弹飞行(即目标飞行器作U型机动后，导弹尾追目标飞行)。

数值仿真计算条件:①目标初始飞行速度为300m/s;②目标机动过载nT=9g，空空导弹最大可用过载nmax=20g;③与传统定义的空空导弹可攻击区相比，在空空导弹射后动态可攻击区仿真计算过程中重新选取了目标飞行状态及其机动类型;④空空导弹开始发射(t=0.0s)的飞行状态参数与空空导弹发射后沿着拦截某目标的弹道飞行10.0s与30.0s后的飞行状态参数如表1所示。

表1 空空导弹的飞行状态参数

数值仿真情形一:1)计算结果如图5所示，图中t=0.0s和t=10.0s分别表示空空导弹传统定义的可攻击区信息和空空导弹发射后沿着拦截某目标飞行10.0s时的可攻击区信息，其中trajectory是空空导弹发射后拦截某目标的弹道飞行10.0s的3D飞行轨迹。对于空空导弹传统定义的可攻击区信息和飞行10.0s时的射后动态可攻击区，均选取目标作Ⅱ型U机动逃逸飞行。其中，图4给出了7km高度的射后动态可攻击区最大可拦截边界。2)计算结果如图6所示，图中t=0.0s和 t=30.0s分别表示空空导弹传统定义的可攻击区信息和空空导弹发射后沿着拦截某目标飞行30.0s时的可攻击区信息，其中trajectory是空空导弹发射后拦截某目标的弹道飞行30.0s的3D飞行轨迹。对于空空导弹传统定义的可攻击区信息和飞行30.0s时的射后动态可攻击区，均选取目标作Ⅱ型U机动逃逸飞行。

图4 导弹飞行10.0s后与Ⅱ型U机动目标飞行对抗轨迹(目标飞行高度为7km)

图5 传统定义的可攻击区与射后10.0s可攻击区(导弹拦截Ⅱ型U机动目标)

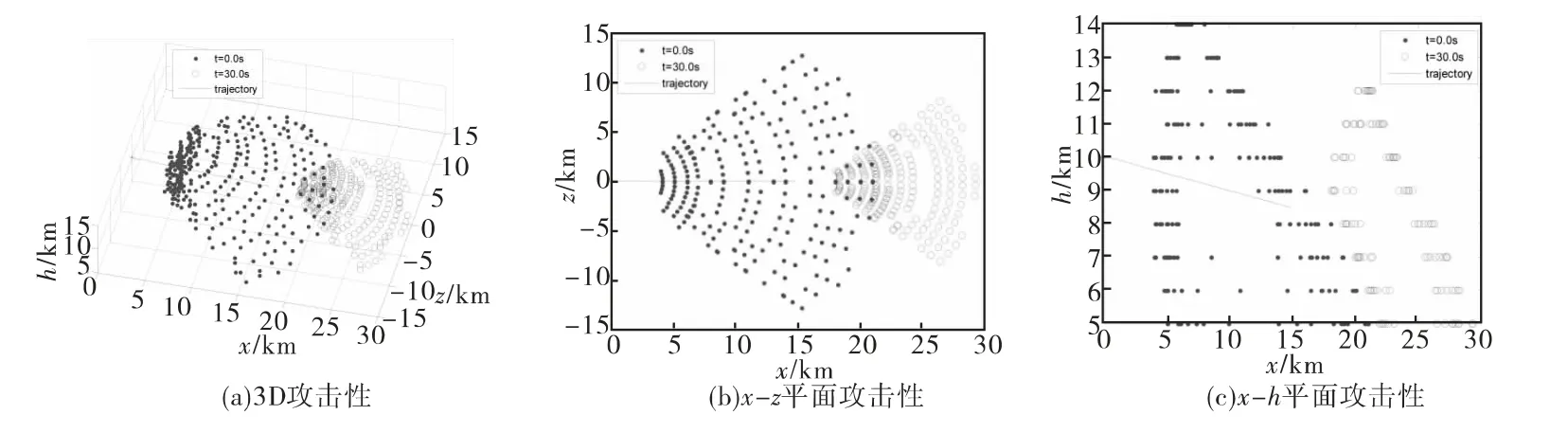
图6 传统定义的可攻击区与射后30.0s可攻击区(导弹拦截Ⅱ型U机动目标)

数值仿真情形二:1)其计算结果如图7所示，图中t=0.0s和 t=10.0s分别表示空空导弹传统定义的可攻击区信息和空空导弹发射后沿着拦截某目标飞行10.0s时的可攻击区信息，其中trajectory是空空导弹发射后拦截某目标的弹道飞行10.0s的3D飞行轨迹。对于空空导弹传统定义的可攻击区信息和飞行10.0s时的射后动态可攻击区，均选取目标作Ⅰ型U机动逃逸飞行。2)其计算结果如图8所示，图中t=0.0s和t=30.0s分别表示空空导弹传统定义的可攻击区信息和空空导弹发射后沿着拦截某目标飞行30.0s时的可攻击区信息，其中trajectory是空空导弹发射后拦截某目标的弹道飞行30.0s的3D飞行轨迹。对于空空导弹传统定义的可攻击区信息和飞行30.0s时的射后动态可攻击区，均选取目标作Ⅰ型U机动逃逸飞行。

图7 传统定义的可攻击区与射后10.0s可攻击区(导弹拦截Ⅰ型U机动目标)

图8 传统定义的可攻击区与射后30.0s可攻击区(导弹拦截Ⅰ型U机动目标)

4.2 3D可攻击区分析

从数值仿真情形一(见图5和图6)中可以看出，空空导弹拦截Ⅱ型U机动目标时，传统定义的空空导弹可攻击区信息并没有包括空空导弹射后动态可攻击区。相比传统定义的空空导弹可攻击区信息，空空导弹射后动态可攻击区的最大、最小可拦截边界随着空空导弹沿着拦截某目标弹道飞行时间的增加而向飞行方向前方推移，侧面边界曲面范围非线性收缩。从数值仿真情形二(见图7与图8)中可以看出，空空导弹拦截Ⅰ型U机动目标时，传统定义的空空导弹可攻击区信息完全包括空空导弹射后动态可攻击区。相比传统定义的空空导弹可攻击区信息，空空导弹射后动态可攻击区的最大可拦截边界随着空空导弹沿着拦截某目标弹道飞行时间的增加而向飞行方向后方推移，最小可拦截边界向飞行方向前方推移，侧面边界曲面范围非线性收缩。综上所述:

①传统定义的空空导弹可攻击区和空空导弹射后动态可攻击区的拦截边界是不同的。前者以载机为参考点，当空空导弹从载机开始发射时，能够拦截的目标空域就已经确定;而后者以空空导弹拦截某目标的弹道飞行tp时间后的位置为参考点，当空空导弹相对此参考点继续飞行时，能够拦截的目标空域。并且目标机动类型是影响前者边界的主要因素，而影响后者边界的主要因素是导弹飞行时间和目标机动类型。

②传统定义的空空导弹可攻击区信息并不一定包括空空导弹射后动态可攻击区，这与重新选取的目标飞行状态及其机动类型有关。当目标与空空导弹处于迎击状态时，空空导弹射后动态可攻击区边界逐渐向传统定义的空空导弹可攻击区内部非线性收缩;当目标处于被空空导弹尾追状态时，空空导弹射后动态可攻击区逐渐向传统定义的空空导弹可攻击区边界之外非线性推移。

4.3 射后动态可攻击区的一个应用

以下给出两枚空空导弹(Missile1和Missile2)同时拦截某一机动目标(Target1)，42.1s后，Missile1成功击毁Target1，但 Missile2仍然具有拦截目标的能力，在导弹的视场范围内重新捕捉到新目标(Target2)，导引头立即锁定Target2，采用三维空间的比例导引律进行制导，继续拦截机动飞行的Target2。其中，Target1作Ⅱ型U机动;Target2飞行方向始终与导弹－目标连线矢量方向相反(即导弹迎击目标)。Missile1的初始飞行状态参数为:V1=300m/s，(x1，h1，z1)=(0，10km，0km)，θ1=0°，ψV1=0°;Missile2 的初始飞行状态参数为:V2=300m/s，(x2，h2，z2)=(0，10km，0km)，θ2=0°，ψV2=0°;Target1 的初始飞行状态参数为:VT1=300m/s，(xT1，hT1，zT1)=(15km，8km，0km)，θT1=0°，ψVT1= － 180°;Target2 的初始飞行状态参数 VT2=300m/s，(xT2，hT2，zT2)=(30km，8km，5km)，θT2=0°，ψVT2= －180°。

图9 空空导弹射后10s后尾追U型机动目标的飞行轨迹

图10 空空导弹加速度

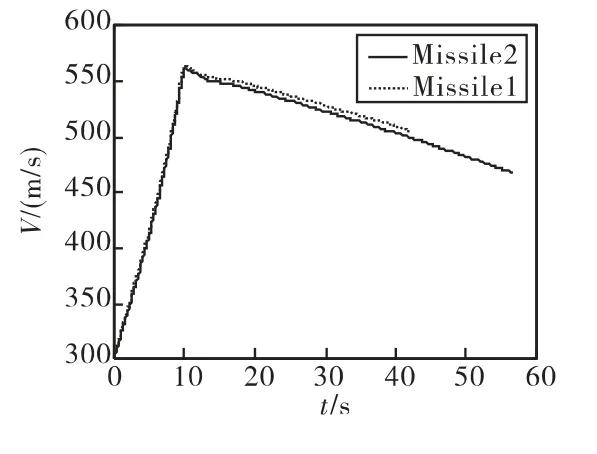
图11 空空导弹速度

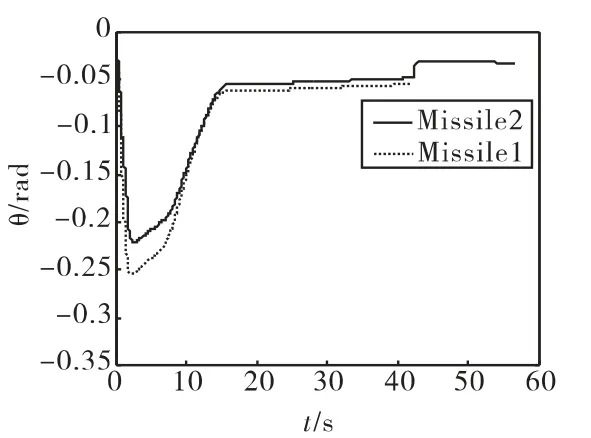
图12 空空导弹轨迹倾角

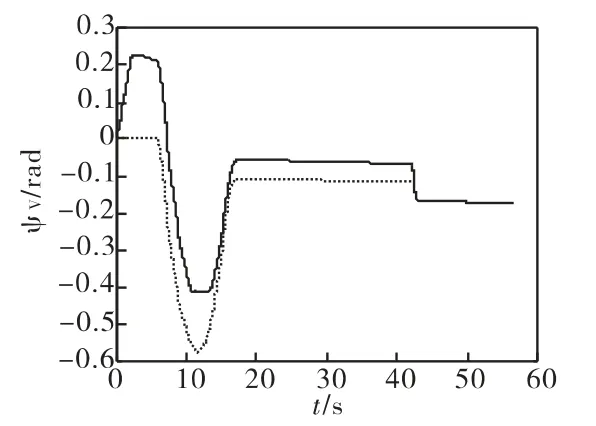
图13 空空导弹轨迹偏角

5 结束语

文中首先提出了空空导弹射后动态可攻击区的新概念，并系统地论述了空空导弹射后动态可攻击区概念的含义;然后给出了空空导弹射后动态可攻击区的飞行数值仿真算法，并数值仿真计算了一些典型情况的射后动态可攻击区。通过与发射时刻动态可攻击区进行对比，得出空空导弹射后动态可攻击区具有以下特点:①发射时刻动态可攻击区与射后动态可攻击区的边界不同，因为二者的参考点选择不同。②空空导弹发射时刻的动态可攻击区并不一定包含射后动态可攻击区，这取决于重新选定的目标飞行状态及其机动类型。

[1]关世义.飞行力学研究的新进展—飞行器攻防对抗研究评述[J].中国科 学，2009，39(3):568－574.

[2]Nan Ying. Algorithm design for F-16 air-to-air missile aiming system(dynamic launch zone，DLZ)[D].Singapore Technologies Aerospace，2003.

[3]Ron Marvin. Aregression method for comparing launch zone ranges derived from different sources[C]//28th National Heat Transfer Conference，1992.

[4]萧保生.空空导弹的攻击区与截获区[J].航空学报，1992，13(2):60 －64.

[5]黄国强，南英，陆宇平.空空导弹擦肩发射全向三维可攻击区计算[J].弹道学报，2011，23(2):37－38.

[6]张平，方洋旺，金冲，等.空空导弹攻击区实时解算的新方法[J].弹道学报，2010，22(4):11 － 18.

[7]王宏伦，张安，张海，等.空－空导弹攻击区的高精度快速拟合[J].航空学报，1997，18(5):631 － 632.

[8]刘代军，高晓光，李言俊，等.中远程空空导弹允许攻击区的快速模拟算法[J].西北工业大学学报，1999，17(4):530－533.

[9]王宏伦，吕庆风.基于模糊逻辑系统的空空导弹攻击区拟合[J].南京航空航天大学学报，2000，32，32(3):305－310.

[10]杜昌平，周德云，江爱伟.一种空空导弹可攻击区快速算法[J].西北工业大学学报，2006，24(6):682－685.

[11]李建勋，张 安，佟明安.导弹非逃跑包络[J].西北工业大学学报，1995，13(3):427 －431.

[12]Grimm，Werner. Optimal'no-escape'firing envelopes of guided missile[C]//American Control Conference，1988:1422－1427.

[13]张安，王宏伦.空空导弹发射包线灵敏度分析研究[J].西北工业大学学报，1994，12(4):567 －571.

[14]吴胜亮，南英，黄国强，等.随机风场与升阻比误差对空空导弹可攻击区的敏感度研究[J].弹道学报，2012，24(2):25－30.