关于不定方程x3+53=Dy2的整数解

廖 军

(文山学院 数学学院，云南 文山 663000)

关于不定方程x3+53=Dy2的整数解

廖 军

(文山学院 数学学院，云南 文山 663000)

设D为奇素数，运用平方剩余、同余式、乐让德符号的性质等初等方法得出了不定方程x3+53=Dy2无x≡0(mod 5)的正整数解的两个充分条件.

不定方程；奇素数；同余；平方剩余；正整数解；乐让德符号

方程x3+a3=Dy2(D是无平方因子的正整数)是一类重要的不定方程，其整数解越来越受到人们的关注.杜先存等[1-4]、张淑静等[5]对a=1的情况进行了系列研究，得到了一系列结果；但a=5时研究的结果还不多见，目前只有很少人进行过研究，其结论主要为：1996年，李复中[6]用简单同余法给出了不定方程x3+125=Dy2的全部非平凡正整数解，其中D>0，且不能被3或6k+1形的素数整数；1998年，李复中[7]用简单同余法给出了一类不定方程x3+(5k)3=Dy2的全部非平凡整数解，其中D>0，无平方因子且不能被3或6k+1型的素数整数；2006年，刘晓敏[8]用二次剩余法给出了不定方程x3+125=Dy2，其中D>0，D含6k+1形素因子，方程x3+125=Dy2无正整数解的充分性条件.本文主要给出了不定方程x3+53=Dy2无正整数解的两个充分性条件.

定理1 若D≡1,49(mod120)为奇素数时，不定方程:

x3+53=Dy2

(1)

无x≡0(mod 5)的Z+解.

证明设(x,y)是方程的一组解，则有方程(1)可化为:(x+5)(x2-5x+25)=Dy2，又gcd(x+5,x2-5x+25)=gcd(x+5,(x+5)2-15(x+5)+75)=gcd(x+5,75)，由于75的正约数有1,3,5,15,25,75，而x≡≢0(mod 5)，故 gcd(x+5,x2-5x+25)=1或3，故方程(1)可分为以下4种可能的情形：

情形Ⅰ：x+5=Du2，x2-5x+25=v2，y=uv，gcd(u,v)=1;

情形Ⅱ：x+5=u2，x2-5x+25=Dv2，y=uv，gcd(u,v)=1;

情形Ⅲ：x+5=3Du2，x2-5x+25=3v2，y=3uv，gcd(u,v)=1;

情形Ⅳ：x+5=3u2，x2-5x+25=3Dv2，y=3uv，gcd(u,v)=1.

以下分别对这四种情形进行讨论：

情形Ⅰ 由第二式得：x=-16,-3,0,5,8,21，则Du2=-11,2,5,10,13,26，无解，故情形Ⅰ不成立.

情形Ⅱ 由u∈Z,得u2≡0,1,4(mod8)，即x=u2-5≡3,4,7(mod 8)，则x2-5x+25≡3,5,7(mod 8)，又x2-5x+25 ≡0(mod 2)，则v2≡1(mod 8)，又D≡1,49(mod 120)，故Dv2≡1(mod 8)，所以3,5,7≡x2-5x+25=Dv2≡1(mod 8)，矛盾，故情形Ⅱ不成立.

情形Ⅲ 由x2-5x+25=3v2配方得：

(2x-5)2+75=12v2

(2)

把x=3Du2-5代入式(2)可得：

3(2Du2-5)2+25=(2v)2

(3)

由情形Ⅳ的第二式配方得：

(2x-5)2+75=3D(2v)2

(4)

把x=3u2-5代入式(4)可得：

3(2u2-5)2+25=D(2v)2

(5)

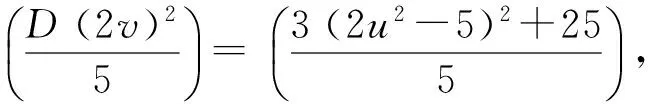
综上：不定方程(1)在题设条件下无x≡0(mod 5)的Z+解.

定理2 设D≡7,43(mod 60)为奇素数时，不定方程：

x3+53=Dy2

(6)

无x≡0(mod 5)的Z+解.

证明设(x,y)是方程(1)的一组解，则方程(1)可化为(x+5)(x2-5x+25)=Dy2，又x≡0(mod 5)，则(x+5,x2-5x+25)=1或3，所以方程(1)可分为以下4种可能的情形：

情形Ⅰ：x+5=Du2，x2-5x+25=v2，y=uv，gcd(u,v)=1;

情形Ⅱ：x+5=u2，x2-5x+25=Dv2，y=uv，gcd(u,v)=1;

情形Ⅲ：x+5=3Du2，x2-5x+25=3v2，y=3uv，gcd(u,v)=1;

情形Ⅳ：x+5=3u2，x2-5x+25=3Dv2，y=3uv，gcd(u,v)=1;

情形Ⅰ 由第二式得x=-16,-3,0,5,8,21，则Du2=-11,2,5,10,13,26，无解，故情形Ⅰ不成立.

情形Ⅱ 由配方得:

(2x-5)2+75=D(2v)2

(7)

把x=u2-5代入式(7)可得:

(2u2-15)2+75=D(2v)2

(8)

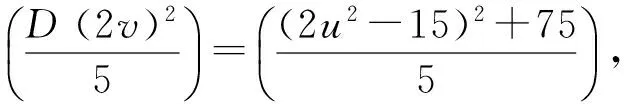
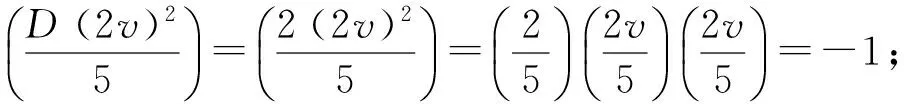
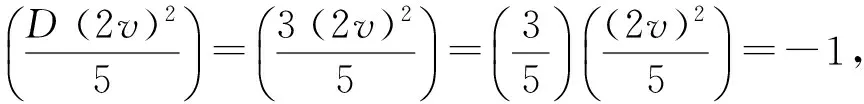
情形Ⅲ 由x2-5x+25=3v2配方得:

(2x-5)2+75=12v2

(9)

把x=3Du2-5代入式(9)可得:

3(2Du2-5)2+25=(2v)2

(10)

情形Ⅳ 由u∈Z,得u2≡0,1(mod 4)，则有3u2≡0,3(mod 4)，即x=3u2-5≡2,3(mod 4)，则x2-5x+25≡3(mod 4)，又x2-5x+25≡0(mod 2)，则v2≡1(mod 8)，又D≡7,43(mod 60)，则3Dv2≡1(mod 4)，所以3≡x2-5x+25=3Dv2≡1(mod 4)，矛盾，故情形Ⅳ不成立.

综上：方程(1)在题设条件下无x≡0(mod 5)的Z+解.

[1] 杜先存,管训贵,杨慧章.关于不定方程x3+1=91y2[J].内蒙古师范大学学报：自然科学汉文版,2013，42(4)：397-399.

[2] 杜先存,万飞,杨慧章.关于丢番图方程x3±1=1267y2的整数解[J].数学的实践与认识，2013，43(15)：288-292.

[3] 杜先存,吴丛博,赵金娥.关于Diophantine方程x3±1=3Dy2[J].沈阳大学学报：自然科学版，2013，25(1)：84-86.

[4] 杜先存,赵东晋,赵金娥.关于不定方程x3±1=2py2[J].曲阜师范大学学报：自然科学版，2013，39(1)：42-43.

[5] 张淑静,杨雅琳,贾晓明.关于Diophantine方程x3+1=3pD1y2[J].山西师范大学学报:自然科学版，2009，23(4)：31-33.

[6] 李复中.关于丢番图方程x3±125=Dy2[J].东北师范大学学报:自然科学版，1996,(3):15-16.

[7] 李复中.关于丢番图方程x3±(5k)3=Dy2[J].东北师范大学学报:自然科学版，1998,(2):16-19.

[8] 刘晓敏.关于丢番图方程x3±p3=Dy2解的讨论[D]. 哈尔滨：哈尔滨理工大学,2006.

OnSolutionoftheDiophantineEquationx3+53=Dy2

LIAO Jun

(College of Mathematics, Wenshan University,Wenshan 663000, China)

LetDbe an odd prime. By using quadratic residue,congruent formula, legendre symbol, two sufficient conditionss are obtained that the Diophantine equationx3+53=Dy2has no integer solutions withx≡0( mod 5).

Diophantine equation;odd prime; congruence;quadratic residue;positive integer solution;legendre symbol

2013-08-21.

云南省教育厅科研基金项目(2012Y270)；文山学院重点学科“数学”建设项目(12WSXK01).

廖军(1977- )，男，硕士，讲师，主要从事初等数学及数理统计的研究.

O156.1

A

1008-8423(2013)03-0275-03