Benjamin-Ono方程的对称性约化

房春梅

(集宁师范学院 数学系,乌兰察布 012000)

Benjamin-Ono方程的对称性约化

房春梅

(集宁师范学院 数学系,乌兰察布 012000)

CK直接方法是求精确解的一种简单有效的方法，该方法的思想是将高维的偏微分方程约化为低维的常微分方程.本文根据此方法获得了Benjamin-Ono方程新的对称性约化，其中包括第一第二和第四Painleve型方程.

C-K直接方法；Benjamin-Ono方程；对称性约化

0 引言

求非线性偏微分方程(组)的对称约化方法很多，如Lie对称方法[1],Clarkson-Kruskal(CK直接方法)[2-3]，以及扩展齐次平衡法[4-5]等等.这些方法都很有效，但其中最为有效的是CK直接约化方法.本文将CK直接约化方法推广到Benjamin-Ono方程[6]:

htt+q(h2)xx+rhxxxx=0

中，获得了该方程的三种形式的对称性约化与相似解，其中包括第一第二和第四Painleve型方程.

对于Benjamin-Ono方程，文献[6]获得了该方程的Backlund变换、非线性叠加公式及无穷守恒律，文献[7-8]获得了该方程的多组精确解.

1 Benjamin-Ono方程的对称性约化

对于Benjamin-Ono方程:

htt+q(h2)xx+rhxxxx=0

(1)

寻找如下形式的对称性约化:

u(x,t)=α(x,t)+β(x,t)φ(ω(x,t))

(2)

其中：α(x,t),β(x,t),ω(x,t)为待定函数.

将式(2)代入式(1)并合并φ(x,t)的单项式以及φ(x,t)的相同导数的同类项可得到：

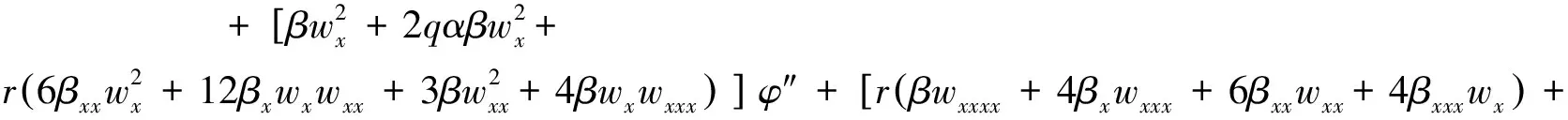
+q(4αxβwx+4αβxwx+2αβwxx)+2βtwt+βwtt]φ′+[rβxxxx+q(2αxxβ+4αxβx+

(3)

要使上述方程约化为φ(w)的常微分方程，那么φ(w)的不同导数的不同次幂的系数均为w的函数.

为了确定待定函数α(x,t),β(x,t),w(x,t)，有几个规则可以利用：

规则1 取φ(4)的系数作为公共因子.

规则2 若α(x,t)=α0(x,t)+β(x,t)Ω(x,t)来确定，则可以取 Ω(x,t)=0.

规则3 若β(x,t)有β(x,t)=β0(x,t)Ω(x,t)则可以取 Ω(x,t)=1.

规则4 若w(x,t)由 Ω(x,t)=w0(x,t)，则Ω(x,t)是任意一个可逆函数，因此可以取Ω(x,t)=w(x,t).

(4)

w(x,t)=xρ(t)+τ(t)

(5)

其中：ρ(t),τ(t)是待定函数，再由式(4)有：

(6)

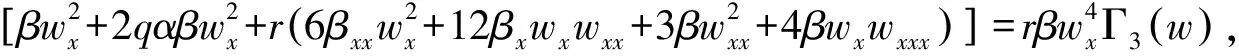
(7)

由式(5)～(7)，式(3)化简成：

(8)

式(8)要化成φ(w)的常微分方程，则满足：

(9)

(10)

(11)

其中：γ1(w),γ2(w),γ3(w)为待定函数.

首先，由于式(9)的左端是x的线性形式，且w(x,t)=xρ(t)+τ(t)，故可以设γ1(w)=Aw+B，其中A,B是常数.

由式(9)～(11)可得：

rρ4[A(ρx+τ)+B]=xρ″+τ″.

令x的不同次幂的系数为零可得：

ρ″=rAρ5

(12)

τ″=rρ4(Aτ+B)

(13)

容易看出：

γ2(w)=2A,γ3(w)=-2(Aw+B)2.

这样便得到了Benjamin-Ono方程的对称性约化:

其中：ρ(t),τ(t)满足式(12)，(13)，φ(w)满足：

φ(4)+φφ″+φ′2+(Aw+B)φ′+2Aφ=2(Aw+B)2.

下面分三种情况进行讨论：

情形1A=0,B=0，此时由式(12)，(13)可解出：

ρ(t)=a1t+a0，τ(t)=b1t+b0.

则可得Benjamin-Ono方程的对称性约化为:

情形2A=0,B≠0，此时由式(12)，(13)可解出：

ρ(t)=a1t+a0，τ″(t)=rB(a1t+a0)4.

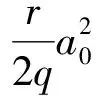
其中φ(w)满足φ‴+φφ′+Bφ=2B2w+c0，此方程等价于 PainleveⅡ方程.

其中φ(w)满足φ‴+φφ′+Bφ=2B2w+c0，此方程等价于 PainleveⅡ方程.

情形3A≠0,B=0，此时由式(12)可得出：

(14)

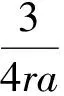
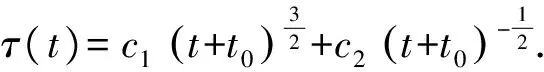
此时可得对称性约化为:

其中φ(w)满足φ(4)+φφ″+φ′2+Awφ′+2Aφ=2A2w2，此方程等价于 PainleveⅡ方程.

2)当A0≠0时，式(14)可利用雅可比椭圆函数求解.

η′2=(1-η2)(1-λ2η2)

(15)

若取D为零，可得到如下的对称性约化:

u(x,t)=(sn2(t+t0;λ)+rA)-1φ(w)-[C(sn2(t+t0,λ)-rA)-

{x+c([3λ2(2-λ2)]t-λ-2E((t+t0,λ))}-[sn(t+t0,λ)×

其中:

φ(w)满足φ(4)+φφ″+φ′2+Awφ′+2Aφ=2A2w2，此方程等价于PainleveⅣ型方程.

[1] Rodica Cimpoiasu,Rodu Constantinescu.Lie symmetries and invariants for a 2D nonlinear heat equation[J].Nonlinear Analysis,2008,68:2261-2268.

[2] 范恩贵.二类变式Boussinesq方程的对称性约化和精确解[J].数学物理学报，1999,19(4)：373-378.

[3] 楼森岳,唐晓艳.非线性数学物理方法[M].北京：科学出版社，2006.

[4] 范恩贵,张鸿庆.齐次平衡法若干新的应用[J].数学物理学报，1997,19(3):286-292.

[5] Fan E G,Zhang H Q.A new approach to Backlund transformation of nonlinear evolution equations[J].Appl Math Mech，1998，19(7):645-650.

[6] 张鸿庆,张玉峰.Benjamin方程的Backlund变换、非线性叠加公式及无穷守恒律[J].应用数学和力学，2001,22(10)：1017-1021.

[7] Wang Z,zhang H Q.A method for constructing exact solutions and application to Benjamin Ono equation[J].Chinese Physics,2005,14:2158-2163.

[8] 套格图桑，斯仁道尔吉.非线性长波方程组和Benjamin方程的新精确孤波解[J].物理学报，2006,55(7)：3246-3254.

SymmetryReductionsoftheBenjamin-OnoEquation

FANG Chun-mei

(Department of Mathematics,Jining Teachers College,Wulanchabu 012000,China)

CK direct method is a simple and effective way to find symmetry reductions of partial differential equations and the idea of the method is to reduce the high dimensional partial differential equation to a low-dimensional ordinary differential equation.According to this method,some new symmetry reductions of the Benjamin-Ono equation are obtained,including the first,second,and fourth Painleve equations.

CK direct method; Benjamin-Ono equation; similarity reductions

2013-04-03.

房春梅(1985- )，女(蒙古族)，硕士研究生,主要从事孤子方程与可积系统的研究.

O290

A

1008-8423(2013)02-0190-04