移动性无线传感器网络吞吐量跨层优化*

丁 凡，周永明

(韶关学院 物理与机电工程学院电子系,广东 韶关 512005)

吞吐量是无线传感器网络的一项重要性能指标，它直接反映了无线传感器网络工作运行的效率[1]。然而目前多数的研究局限于所有传感器节点都是静止的情况，不能满足某些需要移动节点的应用，比如监测野生动物的生活时，节点总是处于不断的运动中。因此有必要对移动性传感器网络（Mobile WSN）的吞吐量进行研究。

LAVERY R J[2]首次建立了Ad hoc网络点对点链路模型，明确了点对点链路模型吞吐量的数学定义式。随后YOO T等人[3]提出了一种数学框架，采用符号速率、数据包长度、调制星座体积三个参数作为优化变量，实现了MQAM调制方式下点对点链路吞吐量的优化。参考文献[4]基于参考文献[2]提出的模型和假设，对链路的吞吐量也作了类似的研究和优化分析。但是参考文献[2-4]在对吞吐量优化分析模型中，接收节点和发射节点是静止的，没有考虑移动情景下吞吐量与节点之间通信距离的关系。

针对上述问题，本文将针对MWSN中如何最大化点对点链路吞吐量这一问题展开研究。为了最大化吞吐量,本文不仅考虑了物理层的符号速率和调制星座体积,而且考虑了MAC层的数据包长度，通过物理层和MAC层参数的联合优化，保证了在不同通信距离下链路的吞吐量能够达到最优。

1 系统模型和假设

为了简化分析，本文只考虑WSN中两个通信节点之间的点对点链路。假定节点发送的单个数据包总长为K＋C＝L(bit)，其中 K为有用信息数据长度，C为循环冗余校验码CRC。同时假设CRC校验能查出所有错误，且忽略应答信号(ACK/NACK)对吞吐量的影响。因此对于一个基于上述模型和假设条件的点对点传输链路，其吞吐量通式为：

其中，b为每个调制符号所包含的比特数，Rs为符号速率，f(b,rs,L)称为包成功传送率(PSR)，它定义为正确地接收到一个数据帧的概率。PSR由下式给出：

这里，Pe为误码率，rs为符号信噪比，定义为：

其中,Pr为信号接收功率，N0为AWGN信道中噪声的半边功率谱密度。

2 移动性无线传感器网络吞吐量优化

在MWSN中，由于节点的可移动性，节点之间的有效通信距离d会发生改变，信号的接收功率以及信噪比也会随之改变。接收功率与收、发节点间的通信距离d的关系如下[6]:

其中,Pt为发送功率，G1为通信距离为1 m时的增益因子，Ml为链路余量，k为路径损耗系数，一般取 3.5。将式(4)代入式(3)可得：

将式(2)、式(5)代入吞吐量的通式(1)中，则有:

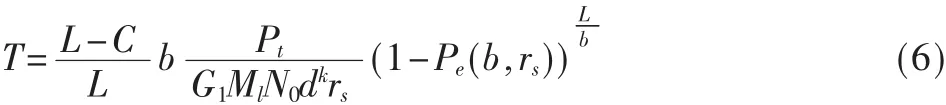
式(6)为AWGN信道条件下，移动性无线传感器网络点对点链路吞吐量的表达式。

2.1 物理层参数优化

2.1.1 符号速率优化

为了找到最优符号速率Rs*,以使得链路的吞吐量达到极大值，对式(6)求关于Rs的偏导数并令该导数为0,即令 ∂T/∂Rs=0,可以得 到：

可见要得到Rs*，应先求得最优符号信噪比rs*。将式(2)代入式(7)中，可以求得 rs*:

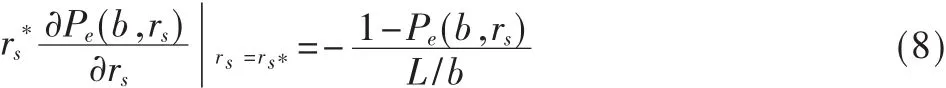
在AWGN信道条件下，采用MQAM调制时，误码率Pe近 似 为[9]：

一旦rs*确定，便可以由式(5)得到相应的最优符号速率 Rs*：

2.1.2 调制星座体积优化

从式(8)、式(9)可以看到调制星座体积 b对 Pe、rs也有影响，因而吞吐量也取决于调制星座体积的大小。同样，对式(6)求关于 b 的偏导数，并令 ∂T/∂b=0，可得:

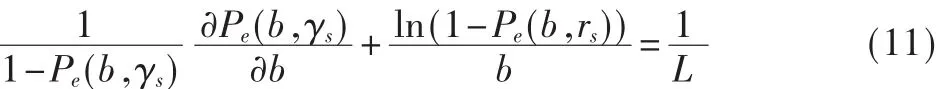
根据不同调制方式下的误符号率Pe,通过求解式(11)，可以得到该调制方式下的b*。

2.2 MAC层数据包长度优化

对式(6)求关于L的导数，可以得到最优数据包长度L*：

在其他参数保持一定的条件下，将式(5)代入式(12)中，可以得到L*为关于d的函数：

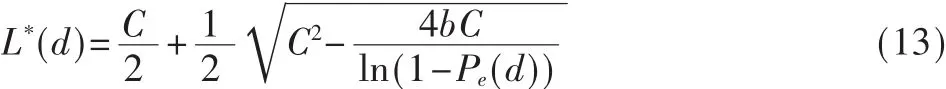
2.3 物理层和MAC层跨层联合优化

为了使链路的吞吐量最大化，必须跨层优化，即在MWSN中,根据通信距离d选择最优配置参数 (L*,Rs*,b*)，自适应地在物理层调整 Rs和 b值，在 MAC层调整L值。最优配置参数 (L*,Rs*,b*)可联立求解式(8)、式(11)、式（12）而得到：

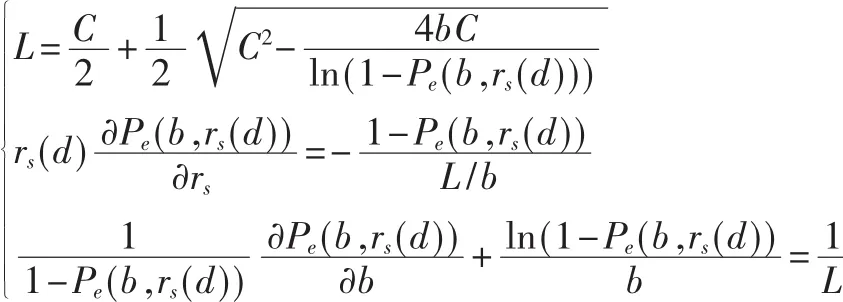
求解方程组可以得到吞吐量函数的驻点(L*,Rs*,b*)，将其代入式(6)中，从而得到移动性无线传感器网络点对点链路吞吐量的最大值：

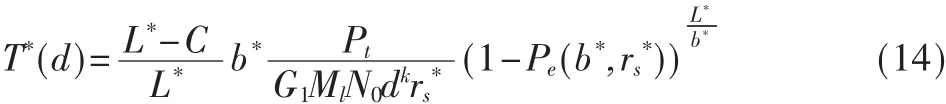
3 仿真结果与分析

为了对上述理论分析进行验证,采用Matlab进行了仿真实验。参照参考文献[2，6],本文仿真中采用的主要参数设置如下：C=16 bit,B=1 MHz,Pt=1 W,G1=30 dB,Ml=40 dB。

3.1 MAC层参数优化仿真

图1比较了在不同通信距离d情况下包长变化时的吞吐量。如图1所示,当d较小时,包长越大,吞吐量越大。这是因为较近的通信距离使得信道条件比较好,信噪比较大,误包率非常小,吞吐量与d无关,而是随着 L的增大而增大。另外，当 L＞＞C时,T≈bRs,即 T的上限值为bRs。以上两点结论均可从图1中得到很好的验证。

图1 不同数据包长L时的吞吐量(b=2,Rs=1 MHz)

求解式(13)可得到不同通信距离下相应的最优数据包长L(d)*，进而得到吞吐量的最优曲线如图1所示。从最优曲线可以看到,当 d＞110 m时,T≈0,此时即使采用最优数据包长也提高不了吞吐量。因此,远距离通信时,仅靠MAC优化并不能使吞吐量最大化。

3.2 物理层参数优化仿真

图2给出了不同符号速率下吞吐量与d的关系曲线。可以看出,当d发生变化时,必须进行速率调整才可能得到最优吞吐量。为此,根据式(8)可求解得到当L=100、b=2时,rs*=9.07 dB。当d发生变化时，应根据式(10)来调节数据速率Rs,确保rs=rs*,以保证得到最优吞吐量。据此得到的最优吞吐量曲线亦显示在图2中。

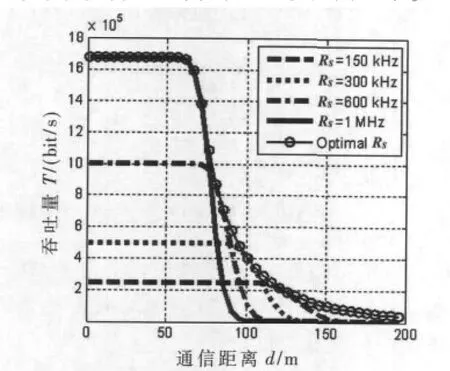
图2 不同符号速率Rs时的吞吐量(b=2,L=100bit)

图3显示了节点移动时b对吞吐量的影响。当d较小时,由于信道条件较好,可采用高阶调制方式来提高系统的吞吐量；而随着d的增大，信道条件恶化，误符号率较大，此时应该采用低阶调制方式以保证最优吞吐量。

3.3 跨层优化仿真及自适应调节策略

为了使链路在不同的通信范围内都能有较高的吞吐量，必须进行跨层优化。 跨层优化后的最优吞吐量曲线如图4所示,同时给出了两种次优吞吐量曲线，以便进行对比分析。从图中可以看到,两条次优吞吐量曲线分别在短距离通信(d＜110 m)和远距离通信(d＞110 m)范围内与最优吞吐量曲线取得一致。可以根据终端节点离发射节点的不同位置，近似认为终端节点处于近距离区或远距离区。在此划分下,为了保证链路的最优吞吐量，可采取如下自适应调节策略：

图4 分层优化和联合优化后的吞吐量对比

(1)近距离区(d＜110 m)：在此区域内信道条件相对较好，可以采用高阶调制方式并联合最优数据包长，可使吞吐量达到最优。最优参数对(b*、L*)可以通过联立求解式(11)、式(13)得到。

(2)远距离区(d＞110 m)：在此区域内信道条件急剧恶化,此时应以尽量降低 Pe为主。由式(9)知，为了尽可能降低Pe,应该采用BPSK,即b=1；同时调节符号速率Rs以使rs=rs*。由式(13)可求解得到在此区域内应采用的最优数据包长L(d)*=L(b=1,rs*)。

通过上述自适应策略配置相应的参数组(b、L、Rs),可以保证接收机节点在移动过程中其链路吞吐量达到最优值。

本文采用跨层优化分析的方法，针对移动性无线传感器网络点对点链路的吞吐量问题作了优化分析。通过选择优化后的物理层参数符号速率Rs并调制星座体积b和MAC层参数数据包长度L,可以优化链路吞吐量。最后提出了一种自适应跨层调节的优化策略，根据该策略自适应调节物理层和MAC层参数,保证了在不同通信距离下链路的吞吐量始终保持最大化。

[1]孙利民,李建中,陈渝,等.无线传感器网络[M].北京：清华大学出版社，2005.

[2]LAVERY R J.Throughput optimization for wireless data transmission.M.S.thesis,Polytechnic University,June 2001.

[3]YOO T,LAVERY R,GOLDSMITH A,et al.Throughput optimization using adaptive techniques.[2012-01-02].http://systems.stanford.edu/Publications/Taesang/Commletters_2005_draft.pdf.

[4]Liu Jian,Sun Jian,Lv Shoutao.A novel throughput optimization approach in wireless systems[C].IEEE ICCT2010,Nanjing,China,2010:1374-1378.

[5]柯欣,孙利民.多跳无线传感器网络吞吐量分析[J].通信学报，2009,28(9):78-84.

[6]CUI S,GOLDSMITH A,BAHAI A.Energy-constrained modulation optimization[J].IEEE Trans.on Wireless Communications,2005，4(5):2349-2360.