高斯－克吕格投影反解的数值变换方法分析

孙卫新，马 俊，2，薛志伟，3，王海洋

（1.信息工程大学 测绘学院，河南 郑州 450052；2.61363部队，陕西 西安 710054；3.63710部队，山西 岢岚036301；4.61892部队，广东 汕头 515071）

高斯－克吕格投影亦称横轴墨卡托投影，于1936年由国际大地测量和地球物理联合会制定［1］，具有等角投影的性质、中央经线与赤道投影后为直线且为投影的对称轴、中央经线投影后没有长度变形的特性。我国现有的比例尺大于1∶50万的地形图和工程测量平面坐标系统大都采用该投影。大比例尺系列地形图一般具有规范的中央经线和投影分带标准，而在工程测量和针对某一制图区域的实践应用中为了降低高斯－克吕格投影带来的长度变形，经常将中央经线选在制图区域的中心，并且分带的标准及采用的椭球体参数也会有所不同。若要对现有采用高斯－克吕格投影的地图资料进行反解变换，一般采用精度较高的解析变换法。但是当不确定原图投影采用的中央经线和椭球体参数的情况下，通常采用数值变换的方法来解决这一问题［2］。

地图投影的数值变换方法在空间数据处理中具有广泛的应用［3］。它的核心是构造逼近函数，不同的变换方法在多项式逼近的稳定性与变换精度方面存在较大的差别。同样的变换方法，不同的共同点分布、多项式次数等因素也会对变换精度及稳定性产生影响。本文针对高斯－克吕格投影的反解，通过具体实验分别采用不同的数值变换方法进行变换，并对各方法变换的精度及稳定性进行对比分析。

1 地图投影数值变换方法

地图投影数值变换方法分为数值变换的一般方法和等角投影的数值变换方法。数值变换的一般方法主要有二元n次多项式和乘积型插值多项式，二元n次多项式多采用二元三次多项式，乘积型插值多项式多采用二元双二次多项式。等角投影的数值变换方法主要包括正形多项式法、差商法、差分法与有限元法，其中正形多项式法因共同点需求数目少、稳定性高、易于编程实现等优势成为以上四种方法中应用最广泛的方法。数值变换方法中多项式的求解包括直接求解和最小二乘法求解两种方式。

1.1 数值变换的一般方法

1.1.1 二元三次多项式

二元三次多项式可描述为

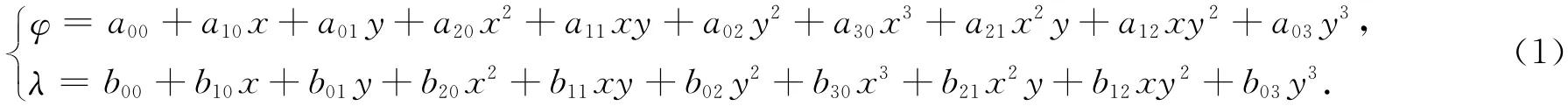
式中：（φ，λ）为地理坐标，（x，y）为原投影坐标，aij，bij（i＝0，1，2，3；j＝0，1，2，3）为多项式系数。

多项式的求解所需共同点的最少数量为10个，概括为线性方程组的求解如下：

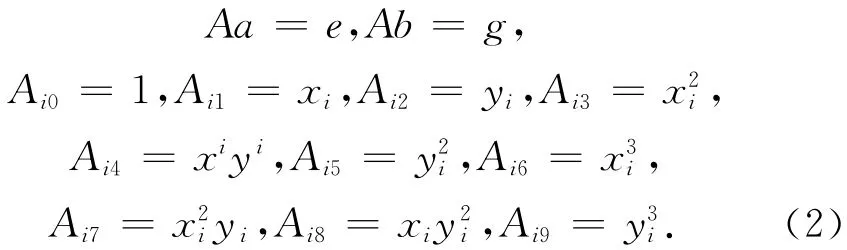
直接求解式（2）中A，e，g分别为

最小二乘法求解时，根据最小二乘法的原理和条件经整理后可得A，e，g分别为

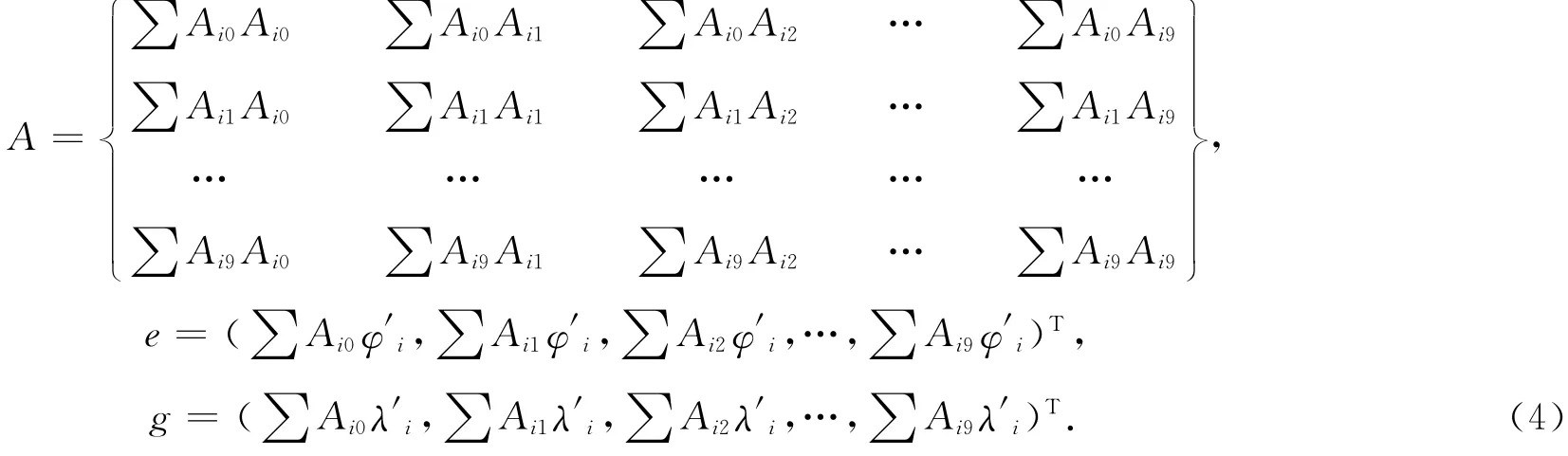
1.1.2 二元双二次多项式

二元双二次多项式的表达式为

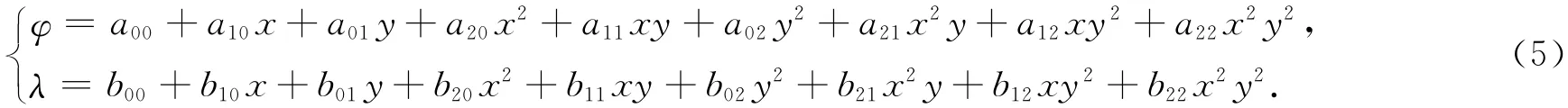
式中：（φ，λ）为地理坐标，（x，y）为原投影坐标，aij，bij（i＝0，1，2；j＝0，1，2）为多项式系数。

二元双二次多项式的求解至少需要9个共同点，其解法与二元三次多项式类似，可同样概括为线性方程组按照直接求解或最小二乘法求解的方式进行求解。

1.2 等角投影数值变换的正形多项式方法

以四次正形多项式为例说明正形多项式的求解。对于正形多项式的直接求解，在变换区域内选取展开点0的坐标（x0，y0）和（B0，l0）与四组共同点坐标（xi，yi）和（Bi，li）（i＝1，2，3，4）。按正形多项式的性质可得线性方程组［4］

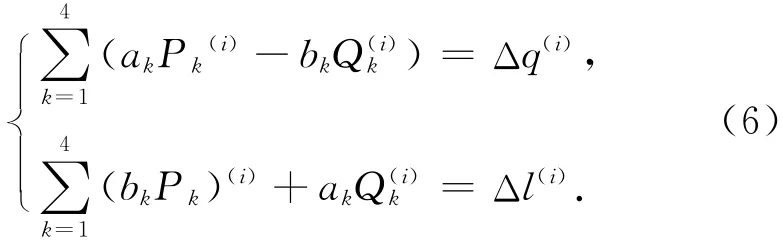
式（6）写成矩阵形式为

式中：

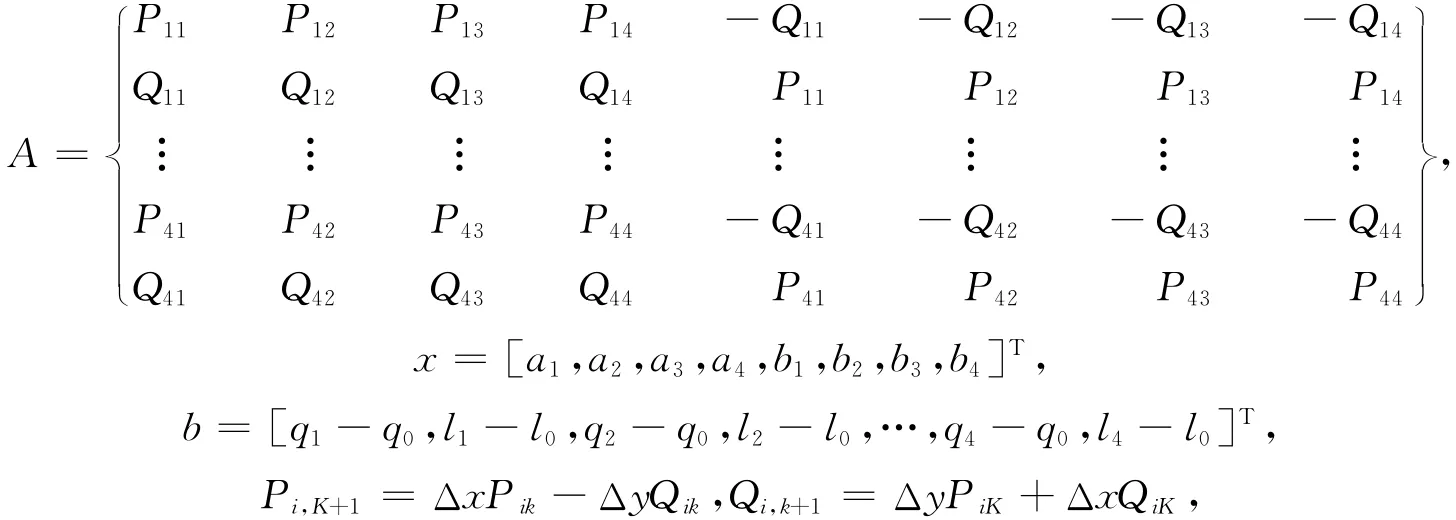
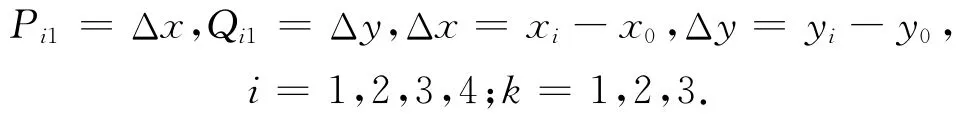
将展开点和4个已知点坐标的纬度B换算为等量纬度q，代入式（7）求解系数ai，bi，将求解系数代入式（6）即得高斯－克吕格投影的反解公式。求得的（q，l）需将等量纬度q换算为相应的地理坐标B。

若用最小二乘法进行求解，已知展开点0坐标（x0，y0）和（B0，l0）及变换区域内m（m＞4）个共同点坐标（xi，yi）和（Bi，li）（i＝1，2，3，4，…，m）。由式（6）根据最小二乘法原理和条件经变换后可得与式（7）相同的形式，其中A，b，i，k变为

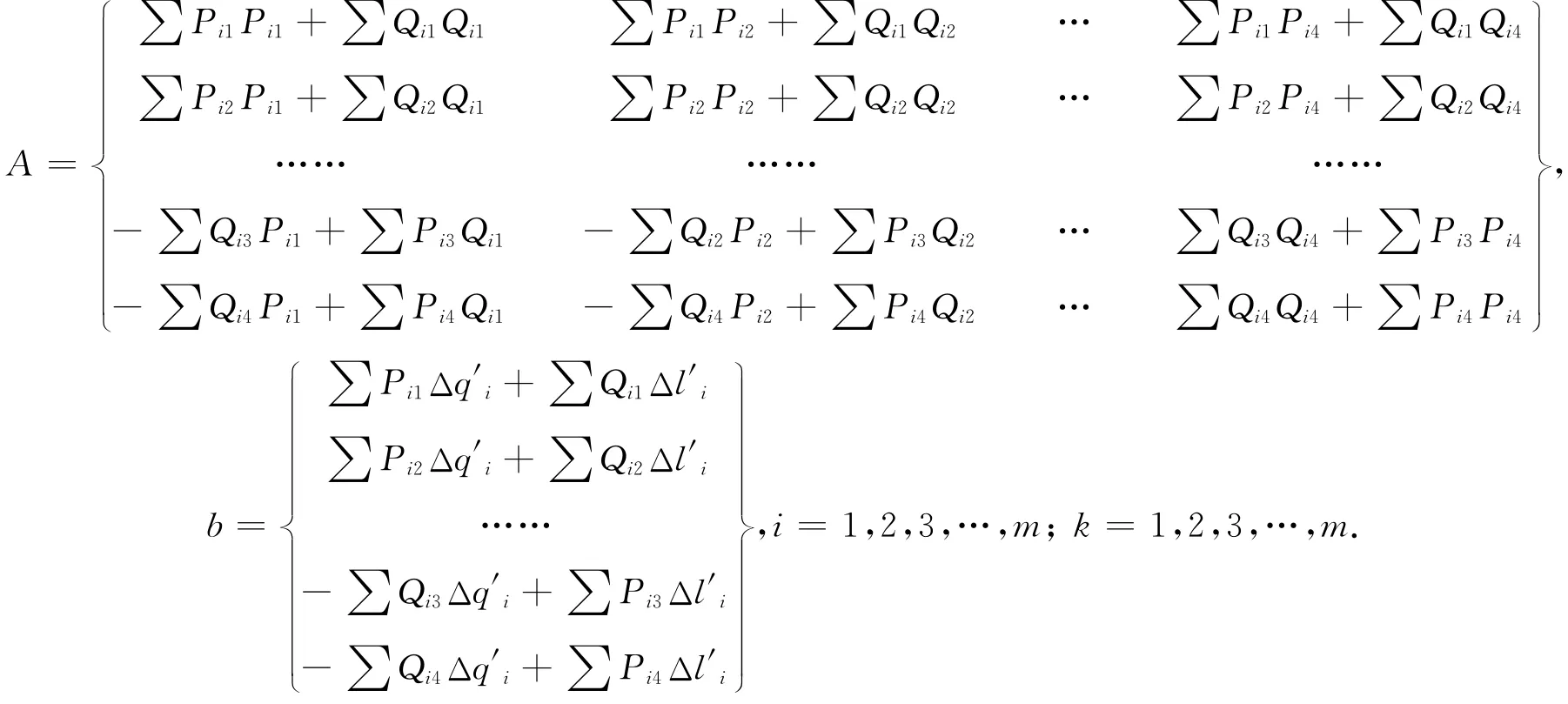
2 实验与分析

实验中地图资料采用的高斯－克吕格投影为6°分带，变换区域范围为经度＋0°～＋6°，纬度＋20°～＋30°，参考椭球体选取克拉索夫斯基椭球［5］，各方法中检查点最大点位误差统一精确到小数点后第9位。以visual studio 2008为开发平台，基于C#语言对以上数值变换方法进行了具体实现。

二元三次多项式和二元双二次多项式已知点分布的两种方案如图1和图2所示。图1与图2中二元三次多项式的直接求解与最小二乘法求解以点1～10为已知点，二元双二次多项式的直接求解与最小二乘法求解以点1～9为已知点。按图2的分布方案，变换的结果产生“畸变”，导致反解结果错误，原因在于共同点的分布过多的对称于中央经线。按图1的分布方案进行反解，图1中点11～20检查点的最大点位误差如表1所示。

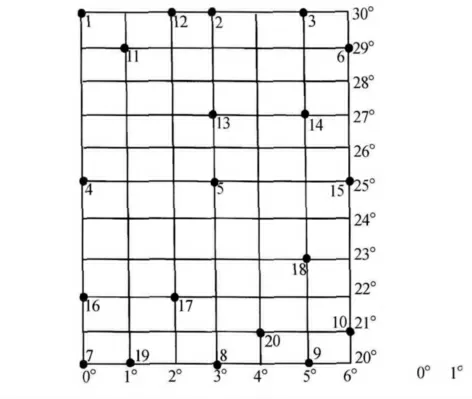
图1 分布方案1

图2 分布方案2

表1 数值变换一般方法检查点最大点位误差

由表1可以看出，采用最小二乘法进行二元三次多项式和二元双二次多项式的求解精度要高于直接求解，但是在已知点数目为所需最少共同点数目的情况下采用最小二乘法进行求解的优势不是特别明显。二元三次多项式的反解精度高于二元双二次多项式，并且通过对实验过程中10个检查点的综合对比，发现二元三次多项式的稳定性也要优于二元双二次多项式。

等角投影正形多项式方法的已知点分布的两种方案如图2、图3所示。图2分布方案中点5为中心点。四次正形多项式的直接求解以点1、3、7、9为展开点，三次正形多项式的直接求解以点2、7、9为展开点，四次和三次正形多项式的最小二乘法求解以除中心点以外的9个点为其他共同点。图3分布方案中点1为中心点。四次正形多项式的直接求解以点2、4、8、10为展开点，三次正形多项式的直接求解以点3、8、10为展开点，四次和三次正形多项式的最小二乘法求解以点2～10为其他共同点。图3分布方案中点11～20为以上两种分布方案的检查点。检查点最大点位误差如表2所示。

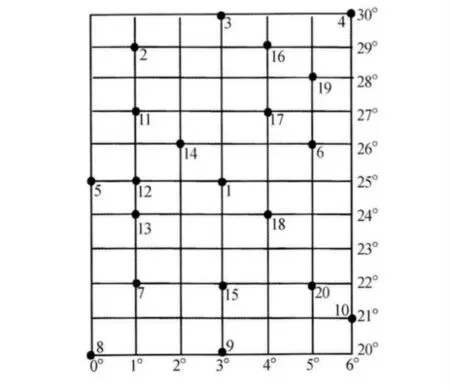
图3 分布方案3

由表2可以看出，共同点数目较多的情况下采用最小二乘法进行正形多项式求解的精度明显高于直接求解。当共同点分布过多的对称于中央经线时会降低求解的精度，但有效地避免了数值变换的一般方法中同样的已知点分布方案所导致的结果错误。对于高斯－克吕格投影的反解变换，四次正形多项式的精度要明显高于三次正形多项式。

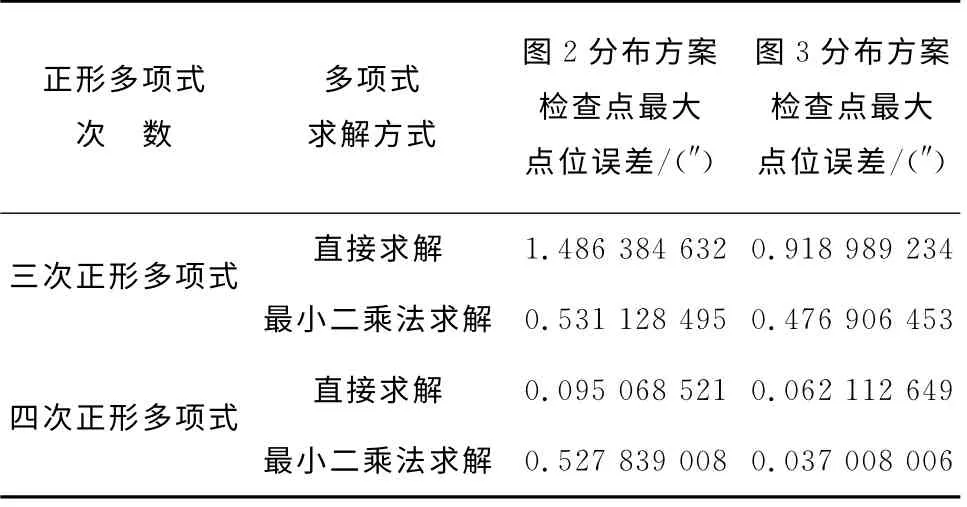
表2 正形多项式方法检查点最大点位误差

3 结束语

本文通过对上述各数值变换方法的实现与结果分析，发现采用数值变换方法进行高斯投影反解对共同点的分布状况要求较高，应尽量避免共同点较多对称于中央经线，特别是数值变换的一般方法。若不确定现有地图资料的中央经线，则要尽量避免已知点对称于图幅中部纵轴线。等角投影正形多项式方法反解的精度和稳定性都要优于数值变换的一般方法。采用最小二乘法能有效地提高反解的精度，降低对共同点原始数据的依赖。因此，在利用数值变换方法进行高斯投影反解应选择正形多项式方法，并且在已知共同点数目允许的情况下尽量选择四次正形多项式并以最小二乘法进行求解。

［1］浦天宏，娄雅斌.GIS采用高斯－克吕格投影技术的研究［J］.鞍山师范学院学报，2008，10（2）：38－41.

［2］吕晓华，刘宏林.地图投影数值变换方法综合评述［J］.测绘学院学报，2002，19（2）：150－153.

［3］李国建，胡鹏.通用的地图投影数值变换［J］.地球信息科学，2001（4）：61－65.

［4］杨启和.地图投影变换原理与方法［M］.北京：解放军出版社，1990.

［5］李国藻，杨启和，胡定荃.地图投影［M］.北京：解放军出版社，1991.