自适应四叉树网格下的N-S 方程数值求解模型
黄筱云 ,李绍武
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 长沙理工大学水利工程学院,长沙 410114;3. 长沙理工大学水沙科学与水灾害防治湖南省重点实验室,长沙 410114)
采用欧拉方法模拟不可压缩黏性流动时,计算精度在很大程度上取决于网格的尺寸.然而,对网格进行全局细化会增加计算机内存用量和计算时间.与同分辨率的均匀网格数值模型相比,自适应网格数值模型能够在保证计算结果精度的前提下有效减少计算网格数量.
与有限单元法和有限体积法采用的自适应三角网格不同,有限差分法采用的是一种按尺寸大小分级的正方形网格.网格等级结构有2 种:一种是自适应网格细分(adaptive mesh refinement,AMR)结构[1-3];另一种是树型网格结构[4],二维情况称为四叉树结构.AMR 结构是将计算区域划分为若干大小不一的矩形子区域,每个子区域再划分为大小均一的正方形网格.有限差分计算从低到高逐层进行,每层计算结果作为下一层计算的边界条件;反过来,自高到低,每层计算结果又用于对下一层计算结果的修正.四叉树结构则对每层计算区域形状不做任何要求,而通过采用特定的有限差分格式直接在叶网格上进行计算.
2003 年,Popinet[5]首先在平衡的树型网格结构上对不可压缩理想流体进行了模拟,其中,压力和速度都定义在网格中心,Euler 方程采用两步投影法求解,压力泊松方程则通过多重网格法来计算.此后,Losasso 等[6]提出一种交错的平衡四叉树网格结构,即将压力定义在网格中心,速度分量定义在网格边上,对不可压缩理想流体进行了模拟,其中,对流项通过半拉格朗日方法求解,泊松方程则采用近似中心差分进行离散,以达到简化计算的目的.2006 年,Losasso 等[7]又进一步提出了基于支撑算子方法[8](support operators method,SOM)的离散格式,将泊松方程在树型网格下解的精度从一阶提高到二阶,且得到的系数矩阵保持对称.到目前为止,应用自适应四叉树网格结构建立的多数流体运动模型主要是基于理想流体运动方程,忽略了黏性项,因此不具普适性.Min 等[9]曾将压力和速度都定义在网格节点上,提出了一种四叉树下偏导数的离散新格式以求解黏性项和压力泊松方程,但泊松方程离散后的系数矩阵为非对称,方程求解难度显著增加.
本文在Losasso 的基础上提出一种平衡四叉树网格下黏性项的新离散方法,并建立了一种新的不可压缩黏性流体运动数值模型.该模型可通过定义在网格节点上涡度值的大小对网格尺度进行自动调整,既保证复杂形状流场区域具有足够网格分辨率,又不显著增加网格数量.此外,新模型采用指针和链表来描述网格层级关系,采用具有二阶精度的无条件稳定MacCormack 方法[10]来计算对流项以保证计算结果具有较高精度.最后,通过单涡、方腔流和圆柱绕流等典型算例来验证新模型的有效性.
1 控制方程
新模型的控制方程为不可压缩黏性流体的N-S 方程,即

式中:ui为速度张量;ρ为流体密度;p为压力;τij为黏性应力张量;gi为体积力张量.对于牛顿流体,黏性应力张量可表示为

式中μ为动力黏性系数.
不可压缩黏性流体的N-S 方程将通过两步投影法进行求解[11].第1 步,计算中间速度,其计算式为
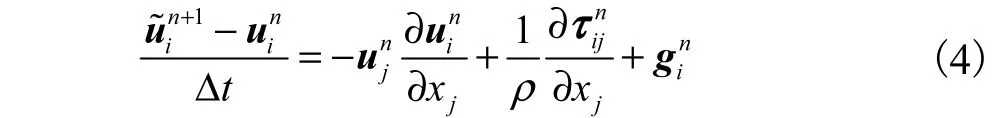
式中Δt 为时间步长.第2 步,将中间速度场投影到散度为0 的平面上以获得最终速度,即

在式(5)的两端取散度,并运用连续性条件式(6),可得

该方程称为压力泊松方程.
2 四叉树网格结构与变量定义空间布置
等级结构网格如图1 所示,其中四叉树网格属于非结构网格,网格形状为正方形.每个正方形网格对应四叉树的一个结点,可以有上一层父网格和下一层子网格(如图2 所示,NE、NW、SW 和SE 分别表示根网格的4 个象限),尺寸最大的网格所在层为0层,对应的节点为根结点,没有子网格的为末端的叶网格.每个0 层网格所包含的全部网格的集合称为一个四叉树结构,若干个四叉树形成的网格结构群称为四叉树森林.每个四叉树网格有4 个角点,相邻角点的连线称为网格的侧边,而侧边上相邻网格节点的连线称为网格的边(图3).只包含一条边的侧边称为最小公共边.包含相同公共边的2 个网格互为邻居.
为叙述方便,引入指针来说明建立四叉树网格结构的基本思路.每个网格有4 个指针指向其4 个子网格,1 个指针指向其父网格.同时,每个网格还有分别指向其4 个角点和4 个侧边的指针.为了方便寻找邻居,每个网格节点有4 个分别指向其4 个象限处叶网格的指针,很明显,T 型节点会有2 个指针指向同一个叶网格.每个最小公共边有2 个指针指向相邻的叶网格.如图4 所示,网格Ⅱ、Ⅲ、Ⅳ和Ⅴ有共同的父网格Ⅰ,网格Ⅳ有4 个子网格Ⅵ、Ⅶ、Ⅷ和Ⅸ.网格Ⅰ和子网格Ⅳ有共同角点C.若网格Ⅱ、Ⅲ、Ⅴ和Ⅶ是叶网格,网格节点E 的4 个指针将分别指向这4 个网格.若网格Ⅸ和Ⅴ是叶网格,网格Ⅸ的右侧边1 是最小公共边,则最小公共边1 的2 个指针分别指向Ⅸ和Ⅴ.在遍历四叉树网结构时,采用链表连接同层的叶网格是十分方便的.
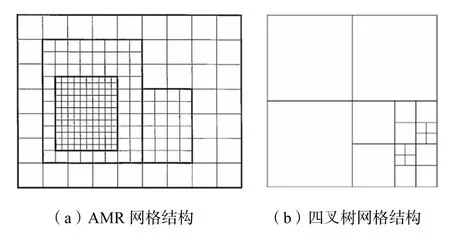
图1 等级结构网格Fig.1 Hierarchical structure of grids
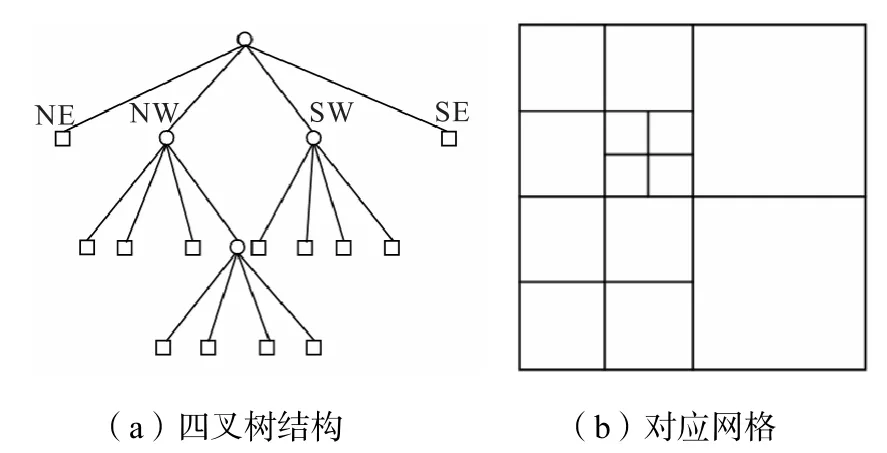
图2 四叉树网格结构示意Fig.2 Quadtree and quadtree subdivision
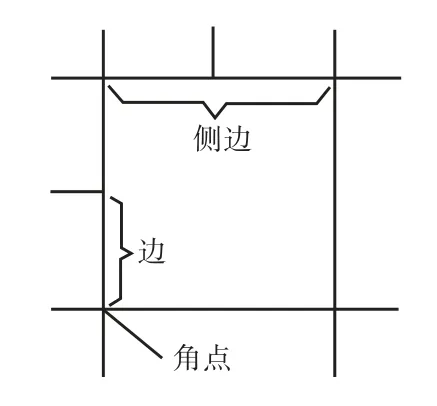
图3 侧边、边和角点Fig.3 Side,edge and vertex
为了确保唯一性,定义某一方位上层数不大于n的所有相邻网格中尺寸最小者为n 层网格在该方位上的邻居.例如,图4 中网格Ⅴ左侧与网格Ⅳ、Ⅸ和Ⅶ相接,但只有Ⅳ被认为是它的邻居.相邻叶网格尺寸之比不超过2 时为平衡四叉树结构.图5 给出平衡前、后两种网格的对比,其中实线代表平衡前的网格,虚线代表通过平衡增加的网格.对矩形计算区域,可先将其划分成大小相同的若干个0 层正方形网格,再对每个网格进行逐层细化,直到满足分辨率要求.

图4 四叉树的等级结构Fig.4 Hierarchical structure of a quadtree
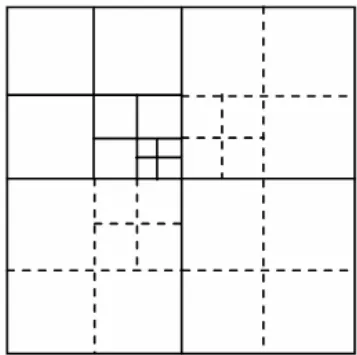
图5 平衡的四叉树网格结构Fig.5 A balanced quadtree
为离散方便,速度和压力采用交错定义,即压力定义在叶网格中心,速度分量定义在最小公共边上(图6(a)).网格侧边上的速度可以通过所包含的最小公共边上的速度递归得到,如图6 中根网格右侧边上的速度u0可从叶网格右侧边上速度递归得到,即有u0=0.5,u2+0.25,u5+0.125(u11+u12).

图6 交错四叉树网格上变量的定义Fig.6 Definition of variables of a staggered quadtree mesh
3 四叉树网格下N-S方程数值求解
3.1 对流项
新模型采用具有二阶精度无条件稳定的MacCormack 方法离散对流项,其基本原理如下所述.

第2 步,根据预测结果采用半拉格朗日方法进行反向运算得到原始时刻的校正值为

第3步,估计预测值的误差e,e=进而获得的最终结果=整个计算过程如图7 所示.在上述过程中,误差矫正可能导致数值不稳定,可采用限制器来修正最终结果,即将最终结果限制在tϕ值范围之内.
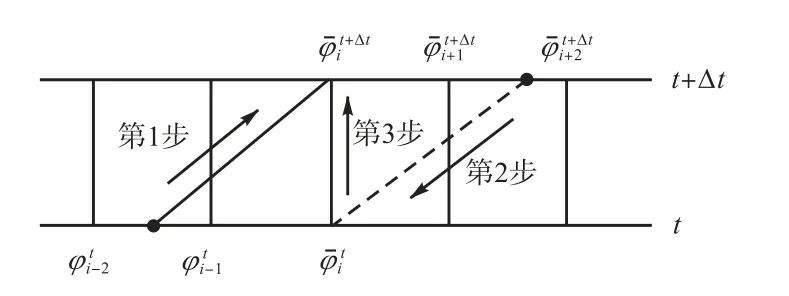
图7 MacCormack方法的计算步骤示意Fig.7 Illustration of the MacCormack method
按照上述原理,在新模型中,对流项的计算过程如下:
(1) 计算t 时刻网格节点上的速度以及最小公共边上切向速度;
(2) 按照式(8)计算t+Δt 时刻最小公共边上法向速度的预测值;
(3) 根据预测值,计算t+Δt 时刻网格节点上的速度以及最小公共边上的切向速度;
(4) 按照式(9)反向计算出t 时刻最小公共边上法向速度的校正值;
(5) 计算误差,获得t+Δt 时刻最小公共边上法向速度的最终值.
网格节点上的速度可通过其周围最大叶网格所在层的速度插值得到,T 型节点上的速度则通过所在侧边端点上的速度线性插值得到.最小公共边的切向速度通过其端点上速度的中心插值得到.
3.2 黏性项的离散
在均匀网格中,黏性项一般可采用中心差分进行离散.然而,在树型网格中,由于相邻叶网格尺寸不一定相同,这种方法不便直接运用.本文提出了一种新方法,其计算细节如下.
(1) 叶网格中心的速度梯度通过对该网格侧边上的速度中心差分得到,如叶网格1 中心的正应力∂ u ∂x 和 ∂ v ∂ y分别为和,叶网格2中心的正应力ux∂ ∂和v y∂ ∂分别为和速度则等于字母上标t、b、l 和r 分别表示网格上、下、左、右侧边,数字下标表示网格(图8(a)).
(2) 网格节点上的速度梯度通过与该节点相邻的最大叶网格所在层上速度的中心差分得到,而T型节点上的速度梯度通过所在侧边端点上的剪应力中心插值得到,如网格节点A 上速度梯度 u y∂ ∂ 和、∂ v ∂ x 可通过和节点B 上速度梯度可通过节点A 和C 上相应值的中心插值得到(图8(a)).
(3) 根据式(3),分别计算出叶网格中心和节点上的正应力和剪应力.
我很小很小的时候,在澡盆里洗澡,洗完了,澡盆被端走,地上有一个圆圆的水印,我就指着水印说:“太阳!太阳!”据说我当时这样说的时候,是十分激动的。夏天,我赤着脚在地上走,脚上有水,地上就有脚印,我又指着脚印说:“小船!小船!”看来我小时候是有些想象力的,而我现在想象力要比那时糟得多。
(4) 若相邻叶网格大小一致,则最小公共边上的正压力梯度通过对叶网格正压力的中心差分获得;否则,令定义在同一方位上与相同叶网格相邻的两个最小公共边上正应力梯度相等,都等于上一级网格侧边上的正应力梯度,该值可通过其相邻的大叶网格和小叶网格的父网格上正应力的中心差分获得,而父网格上正应力通过其子网格上正应力的中心插值得到,如网格1 左侧边上的正压力梯度为

网格10 和11 下侧边的正应力梯度与网格2 上侧边的正应力梯度相等,等于对网格5 和2 上正应力的中心差分(图8(a)),即
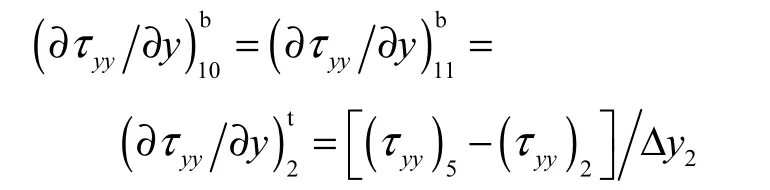
其中

(5) 最小公共边上的剪应力梯度通过其端点上剪应力的中心差分获得,在同一方位上与相同叶网格相邻的两个最小公共边上剪应力梯度也相等.
为了保证计算的稳定性,时间步长取
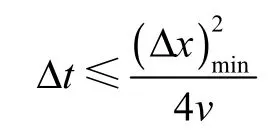
式中:(Δx)min为最小网格尺寸;v 为运动黏性系数.
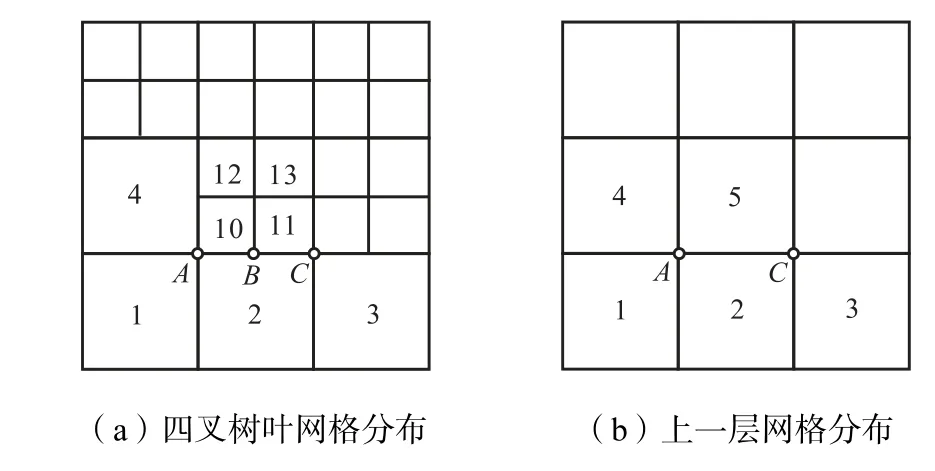
图8 四叉树中不同层的网格Fig.8 Meshes in different levels of quadtree
3.3 压力泊松方程的离散
将式(7)写成
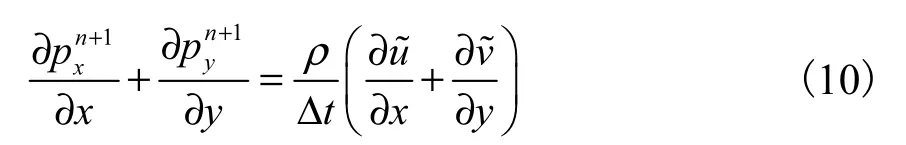
对于相邻叶单元大小一致的情况,定义在侧边上的压力梯度可直接采用中心差分格式进行离散.以图9 为例,网格1 上侧边的压力梯度为

但是,对于相邻叶单元大小不一致的情况,不能直接使用中心差分格式.这里采用一种基于SOM 的新方法.按此方法,定义在叶网格1 和2 之间的网格侧边上的压力梯度为
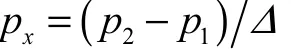
式中Δ为大小叶网格尺寸的平均值.叶网格1 右侧边上的压力梯度则通过对其包含的最小公共边上的压力梯度的加权平均得到,即
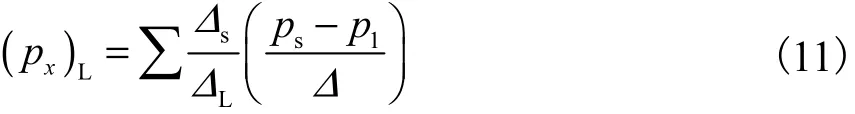
式中下标s 和L 表示小网格和大网格.为了保证计算结果具有二阶精度,小叶网格2 左侧边上的压力梯度采用与大叶网格1 右侧边上一致的压力梯度,即
通过上述处理,压力泊松方程的系数矩阵的对称性也能得到保证,可以采用ICCG 算法求解.
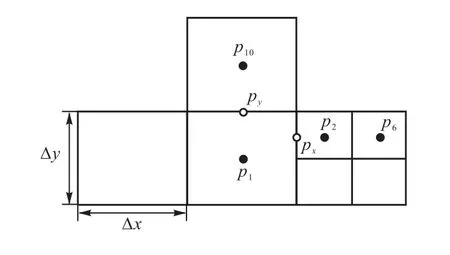
图9 离散泊松方程时变量的定义Fig.9 Definition of variables of discretized Poisson equation
4 网格的适时调整
为了保证计算精度和减少计算量,在计算过程中需要对网格尺度进行适时调整,方法是根据定义在网格节点上的涡度τ值的大小来进行判断.涡度

在计算区域Ω内,若父网格C 中所有网格节点上的τ值都小于阈值τ0,则将其子网格进行合并;若叶网格C 上存在大于阈值τ0的涡度,则该网格需要细分.合并和细分的过程将分步进行,即按四叉树的结构先从上往下对满足条件的父网格进行合并,再从下往上对满足条件的叶网格进行细化.调整完毕后,再将生成的四叉树网格进行平衡化处理.网格细分时,网格侧边上新节点的速度通过侧边端点上速度中心插值得到,网格中心处新节点的速度则通过网格四周节点上速度线性插值得到,新生成的最小公共边上的法向速度则通过其端点上相应速度线性插值得到.
5 算 例
5.1 泊松方程
本算例将讨论新模型中泊松方程的求解精度.考虑泊松方程
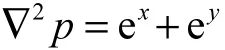
其真解为

取尺寸为1×1 的计算区域,初始网格层数是4,初始最大网格尺寸是0.125×0.125,初始网格划分如图10 所示.分别用不同分辨率的网格进行计算,显然网格分辨率越高计算结果越精确.根据计算结果可以获得数值计算的误差和精度(表1),从中可以看出,格式的精度超过二阶,其中,分辨率n2~m2表示最粗网格的分辨率是n2,最细网格的分辨率是m2.
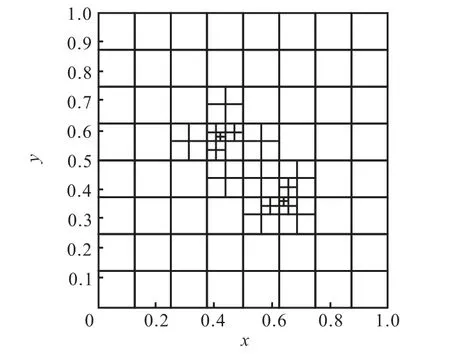
图10 四叉树网格结构(分辨率82~642)Fig.10 Sketch of quadtree mesh(in 82—642)

表1 泊松方程的计算精度Tab.1 Computational accuracy of the Poisson equation
5.2 单涡流
本算例通过模拟区域Ω=[0,π]×[0,π]内雷诺数为1 的单涡流动来分析新模型在四叉树网格下的数值精度.单涡流的真解为
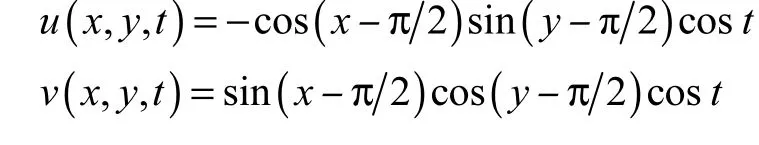
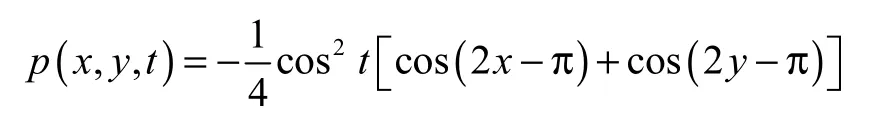
体积力的表达式为
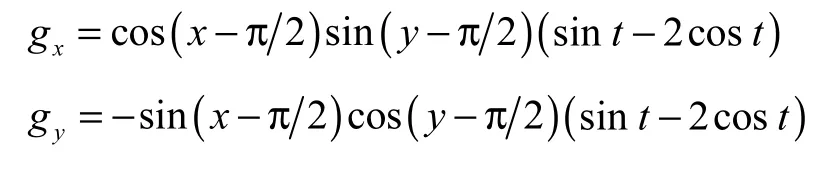
初始网格划分如图11 所示,网格层数为4 层,最大网格为0.785,4×0.785,4.计算时长为π.表2 给出了最终时刻速度数值误差(L2误差为二阶范数误差,L∞为无穷范数误差)和精度结果,可以看出新模型给出的速度具有一阶以上精度.图12 给出了单涡流流线的数值计算结果.
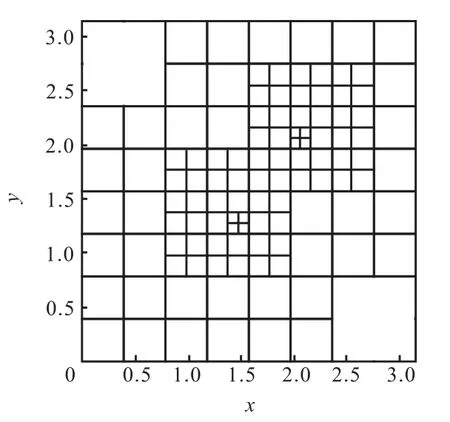
图11 四叉树网格结构(分辨率42~322)Fig.11 Sketch of quadtree mesh(in42—322)

图12 单涡流流线数值计算结果Fig.12 Snapshot of the streamline of single vortex flow

表2 单涡流动速度的计算精度Tab.2 Computational accuracy of velocities in single vortex flow
5.3 方腔流
本算例对Ghia 的二维方腔流算例[12]进行模拟.计算区域大小为1×1(图13).计算区域上边界为剪切边界,剪切速度大小恒为1,其他边则为无滑移边界.雷诺数取为1,000,网格调整阈值τ0同样设为0.04.初始时刻,整个计算区域被均匀地分成64×64个正方形网格.预设网格总层数为3.计算时长为50,s.
计算出的流线和网格变化如图13 所示,可以看出,由于顶部边界的剪切作用,附近的网格始终保持最细状态;在整个流动发展过程中,部分区域网格随涡度增加自动加密,又随涡度减小而恢复初始分辨率.
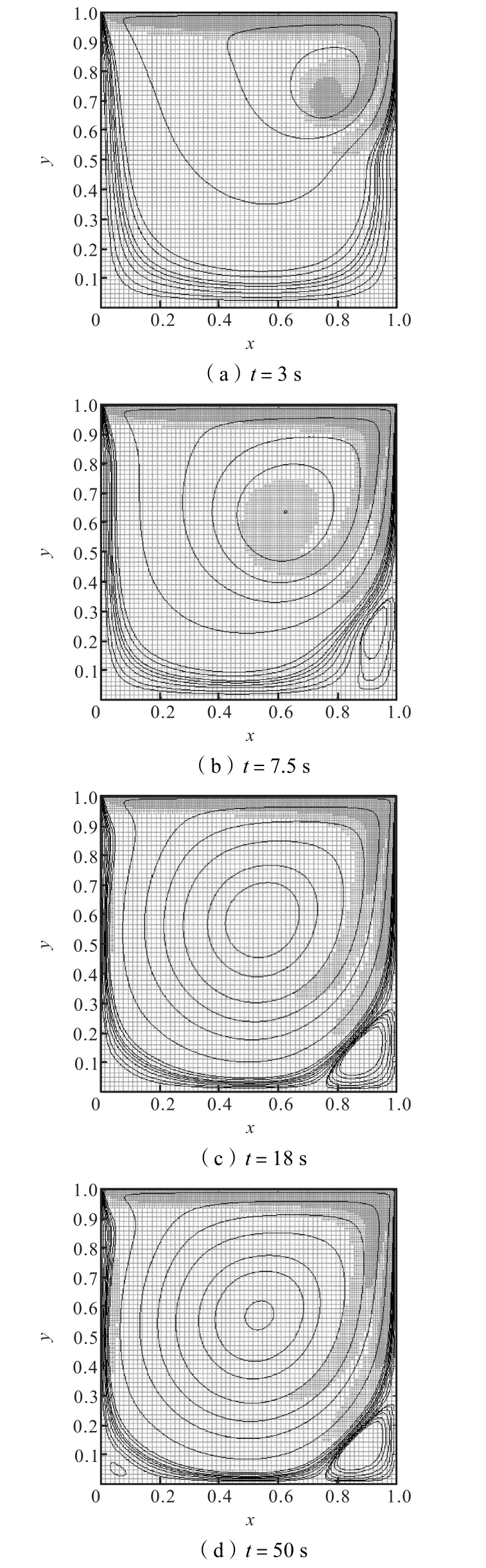
图13 不同时刻流线和网格分布(分辨率为642~2562)Fig.13 Snapshots of the streamline and meshes at different times(in 642—2562)
图14给出了稳定状态时不同分辨率下获得的中轴线上速度分布与Ghia 的计算结果(分辨率为1282)的对比情况,可以看出,网格分辨率为642的计算结果与Ghia 的计算结果偏差较大,而分辨率为2562的结果与Ghia 的计算结果最接近,自适应格分辨率为642~2562的结果与分辨率为2562的结果相差无几.表3 给出了各类网格下网格数量、泊松方程求解矩阵阶数和计算时间的比较,可见自适应网格下网格数量和消耗的计算时间都显著降低.虽然分辨率为642~2562的自适应网格下系数矩阵的最大阶数与分辨率为1282的均匀网格下系数矩阵的阶数接近,但由于自适应下系数矩阵阶数不断变化,且相同阶数下矩阵中非零元素的个数多于均匀网格下的个数,迭代步数会有所增加,计算时间也相应增加.此外,网格的自动调整也会消耗一定的计算时间.
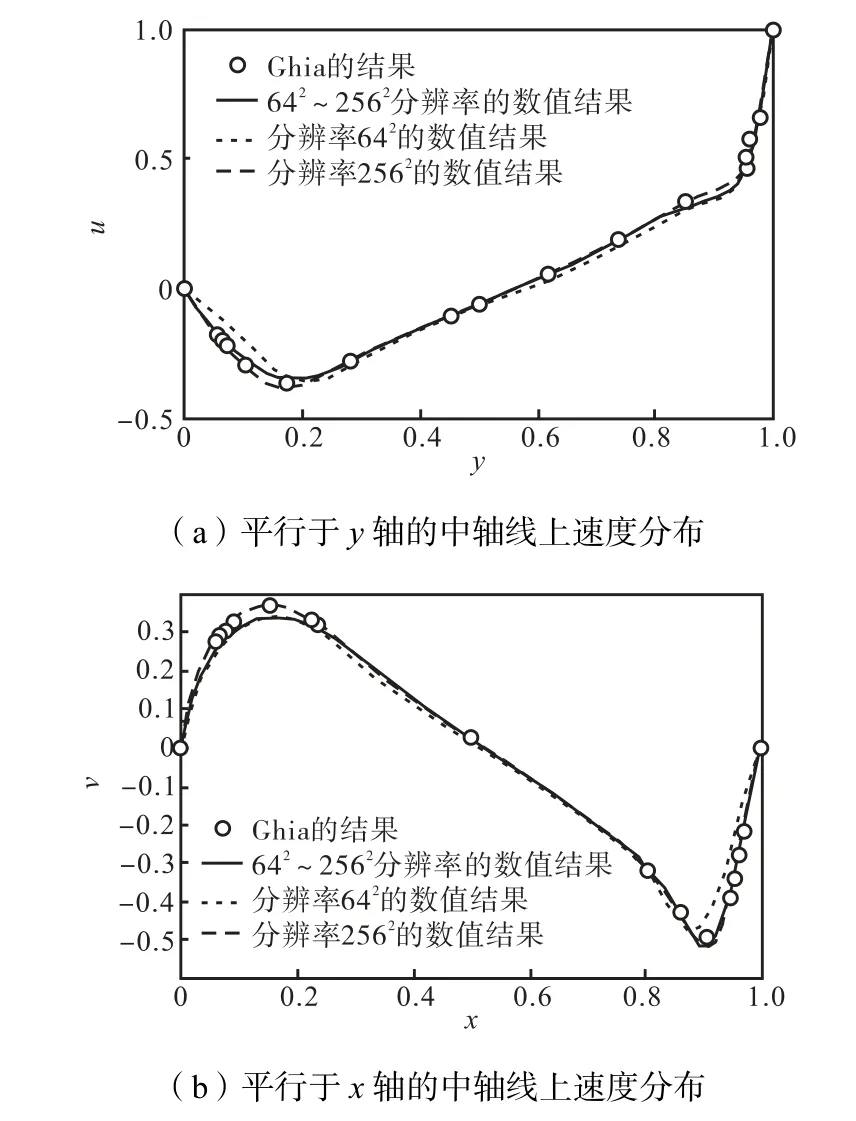
图14 中轴线上速度分布的计算结果与Ghia计算结果的比较Fig.14 Comparisons of velocities along central axes between numerical results and solution of Ghia
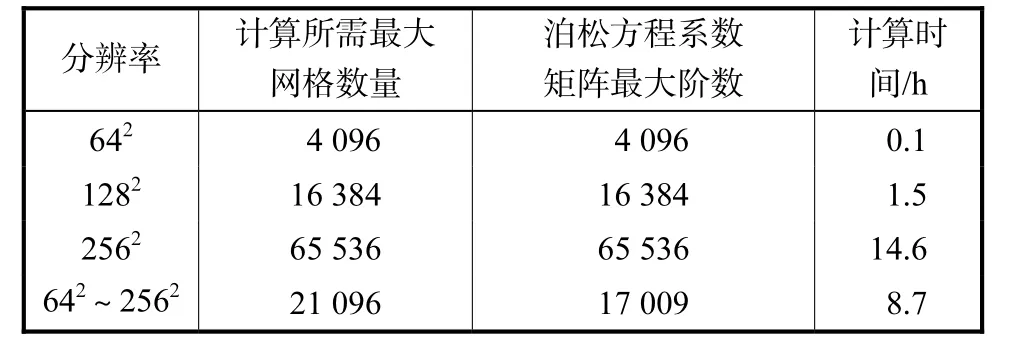
表3 自适应网格与均匀网格下方腔流计算所需网格与时间比较Tab.3 Comparisons of the number of meshes and the computational time in adaptive mesh and uniform mesh
5.4 圆柱绕流
计算区域如图15 所示,无量纲长度为25,无量纲宽度为20.圆柱位于(5,10)处,其直径D=1,Ls=10,Le=5,Lr=20.计算区域左边界为入流边界,入流速度大小为1.右边界为出流边界,上下两个边界为自由滑移边界,圆柱表面为无滑移边界.四周压力边界条件设为零梯度边界条件.
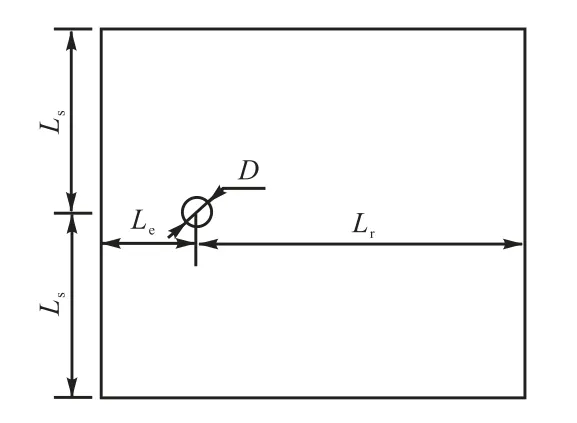
图15 计算区域示意Fig.15 Sketch of computational domain
本算例雷诺数取为200,网格调整阈值τ0仍为0.04.初始时刻整个计算区域分成100×80 个正方形网格.固壁边界按阶梯边界近似处理.为了较好地刻画圆柱,初始时刻对圆柱周围一定范围内的网格进行了加密处理,最大网格尺寸为0.025,预设最大层数为4.表4 给出了圆柱几何特征值比与加密次数的关系.从图16 可以看出,网格能够很好地在涡旋处进行细分,最小网格变化与涡旋运动保持一致,在远离涡街的区域,网格保持不变,这样可使网格数量大大减少.图17 给出了t=62.5,s 时刻流线分布情况.
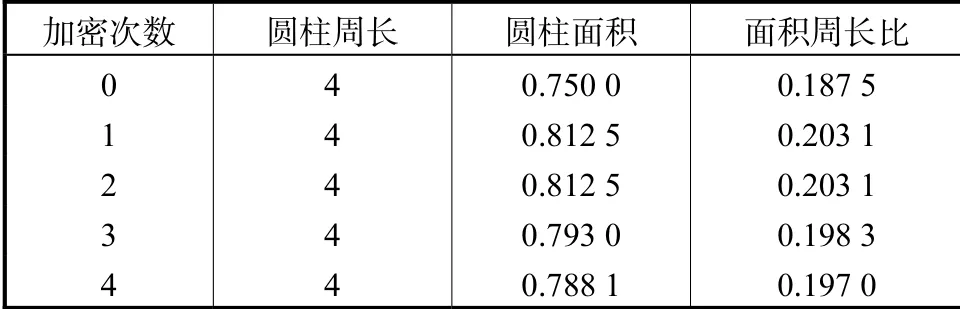
表4 圆柱几何特征值比与加密次数的关系Tab.4 Variation of the geometrical characteristic value ratios of cylinder with the refinement times
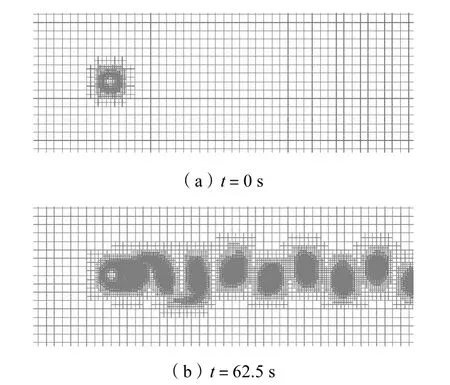
图16 不同时刻网格分布情况Fig.16 Snapshots of cell configuration at different times

图17 t=62.5,s 时的流线分布Fig.17 Snapshot of streamlines at t=62.5,s
图18给出了计算的拖曳力系数CD和升力系数CL随时间变化的过程.拖曳力系数CD和升力系数CL计算式为

式中:FD和FL分别为拖曳力和升力;fρ为流体密度;∞u 为入流边界的速度.在稳定的涡街状态,计算出的拖曳力系数最大值为1.390,最小值为1.233,平均值为1.301,与Wille[13]的试验结果值1.3 十分接近.升力系数则在0.623 和-0.611 之间振荡.
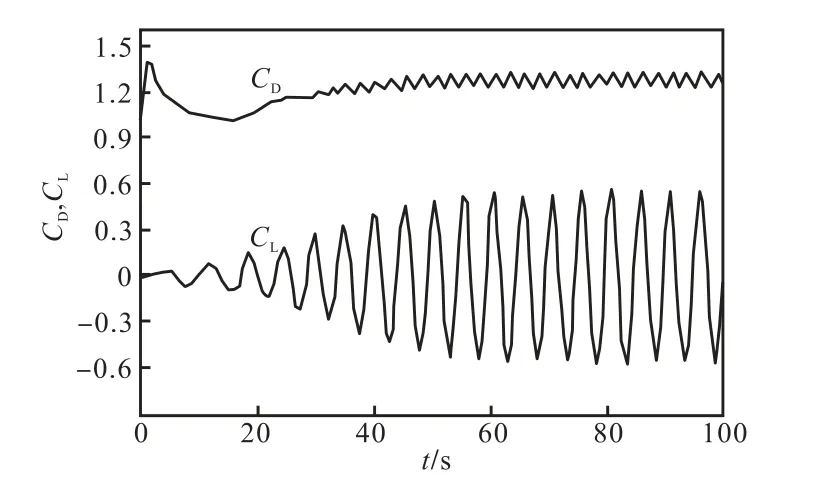
图18 计算出的拖曳力系数和升力系数变化过程Fig.18 Numerical results of drag and lift coefficients of flow over a circle cylinder
6 结 论
(1) 通过数值试验,证明所提出的自适应四叉树网格下的水流模型中的泊松方程解可以达到二阶精度,速度精度在一阶以上.
(2) 方腔流算例的计算结果表明,自适应网格的网格数量比同分辨率均匀网格下的网格数量减少2/3以上,系数矩阵的阶数要减少3/4,计算时间要减少近一半,而计算的中轴线上流速分布基本接近.
(3) 圆柱绕流算例中所得的拖曳力系数和升力系数与经典结果基本一致.
(4) 所有算例的计算结果均表明,模型可以很好地根据设定的网格加密及合并控制指标完成网格的细分和合并.
[1]Berger M J,Oliger J. Adaptive mesh refinement for hyperbolic partial differential equations[J]. Journal of Computational Physics,1984,53(3):484-512.
[2]Howell L H,Bell J B. An adaptive mesh projection method for viscous incompressible flow[J]. SIAM Journal on Scientific Computing,1997,18(4):996-1013.
[3]Martin D F,Colella P,Graves D. A cell-centered adaptive projection method for the incompressible Navier-Stokes equations in three dimensions[J]. Journal of Computational Physics,2008,227(3):1863-1886.
[4]De Berg M,van Kreveld M,Overmars M,et al. Computational Geometry Algorithms and Applications[M].Berlin:Springer,1999.
[5]Popinet S. Gerris:A tree-based adaptive solver for the incompressible Euler equations in complex geometries[J]. Journal of Computational Physics,2003,190(2):572-600.
[6]Losasso F,Gibou F,Fedkiw R. Simulating water and smoke with an octree data structure[C]//Proceedings of SIGGRAPH 2004 Conference, Association for Computing Machinery's Special Interest Group on Computer Graphics and Interactive Techniques .San Antonio ,New York:ACM Press,2004:457-462.
[7]Losasso F,Fedkiw R,Osher S. Spatially adaptive techniques for level set methods and incompressible flow[J]. Computers and Fluids,2006,35(10):995-1010.
[8]Lipnikov K,Morel J,Shashkov M. Mimetic finite difference methods for diffusion equations on nonorthogonal non-conformal mesh[J]. Journal of Computational Physics,2004,199(2):587-597.
[9]Min C H,Gibou F. A second order accurate projection method for the incompressible Navier-Stokes equations on non-graded adaptive grids[J]. Journal of Computational Physics,2006,219(2):912-929.
[10]Selle A,Fedkiw R,Kim Byungmoon,et al. An unconditionally stable MacCormack method[J]. SIAM Journal on Scientific Computing,2008,35(2):350-371.
[11]Chorin A J. Numerical solution of the Navier-Stokes equations[J]. Mathematics of Computation , 1968 ,22(104):745-762.
[12]Ghia U,Ghia K N,Shin C T. High-resolutions for incompressible flow using the Navier-Stokes equations and multigrid method[J]. Journal of Computational Physics,1982,48(3):387-411.
[13]Wille R. Karman vortex streets[J]. Advances in Applied Mechanics,1960,6:273-287.

