无线多跳网络中SVC 视频流传输的分布式优化方法

由 磊，雷建军，王丕超

(天津大学电子信息工程学院，天津 300072)

经过可伸缩编码(scalable video coding，SVC)的视频流包含1 个基本层和多个增强层，可以在一定程度上根据所处的传输环境实现灵活的速率和视频质量的自适应调整[1-2]．近年来，SVC 视频在无线网络中的传输问题得到广泛关注．但目前的研究主要集中在单跳无线网络[3-6]，如蜂窝网中基站可以集中式地控制整个小区的资源调度和为多个用户选择SVC 视频流传输的内容．无线多跳网络(如无线网格网和无线传感器网络[7-8])具有成本低、部署快、可靠性高以及可覆盖边缘或环境恶劣的区域等优点，是实现未来无处不在的接入网和物联网的潜在技术之一．然而，由于节点功率受限、上层可用网络传输容量(能力域)与底层资源分配的紧耦合性，以及要求传输协议具有可扩展性和服务质量保证等特点[9]，SVC 视频在无线多跳网络中传输面临着更多挑战．本文研究无线多跳网络SVC 视频流传输中2 个重要性能参数(网络功率消耗和传输视频质量)的最优权衡(trade-off)及其分布式优化的实现问题．通过对原问题进行对偶分解和采用次梯度算法求解，实现了底层资源分配(带宽和功率)与上层SVC 视频流传输内容选择的最佳匹配，同时得到了一个可分布式执行的跨层传输优化算法．

1 系统模型和问题描述

1.1 系统模型和假设

一个无线多跳网络的拓扑可以用有向图G =(V,E)来表示，其中V 表示节点集合，而E 表示无线链路集合．用S 表示发送SVC 视频的源节点集合．所有的SVC 视频都需要发送到某个已知的汇聚(sink)节点上．集合V、E 和S 的元素分别用n、l 和m表示，其元素数分别为N、L 和M．另外，节点i 和节点j 之间的链路用(i，j)表示．

由于无线信道的干扰，同时发送信息的邻近链路必须分配不同的频带以避免干扰，而在相邻较远的链路上可以进行频率重利用．本文在相同的频带上采用节点独占干扰模型(node exclusive interference model)[10]，该模型只允许节点的一条链路在某段频带上发送或接收信息．定义网络中不能在同一频带上传输的链路组成一个互干扰链路集．对于节点独占干扰模型来说，网络中共有N 个互干扰链路集．本文的优化方法很容易应用到其他的干扰模型中．

定义一个N × L链路互干扰矩阵Χ ．如果链路l属于互干扰链路集n，则xnl= 1，否则 xnl= 0．假设网络的可用频带带宽为b，定义 W =[ w1,…,wL]T为各无线链路的带宽分配矢量，则W 必须满足

其中 B =[b,…,b]T．

定义 P =[ p1,…,pL]T为各无线链路上功率分配矢量，hl为链路l 的无线信道增益．本文假设在整个优化过程中无线链路的信道增益不发生变化．链路l 的传输速率 fl由分配给它的功率和带宽决定，可以根据香农公式计算为

式中Θ为链路速率与香农公式间的差距(由于采用一定的信道编码)；N0为接收端噪声功率谱密度．用Γ表示网络资源分配和链路速率矢量 F=[ f1,…,fL]T的可行取值域，则有

SVC 是一种可伸缩的分层视频编码，可以通过丢弃低优先级的增强层数据来适应可变的传输环境，达到最优率失真性能[1-2]．SVC 标准允许空间、时序和质量上的编码可伸缩性．本文采用质量可伸缩编码中的“ 中等粒度可伸缩(medium grain scalable ，MGS)编码”．关于MGS 视频编码读者可参考文献[1-2]．假设SVC 源节点m 需要发送的视频包含 Im个帧，每个帧被编码成1 个基本层和T 个MGS 层．定义为节点m 的SVC 视频帧传输策略矢量，其中= 0表示帧 z 只发送基本层，而= t (t ≤T)表示帧z 发送基本层和前t 个MGS 层．用峰值信噪比(peak signal-to-noise ratio，PSNR)作为视频质量指标．SVC 视频源m 的PSNR(qm)是Πm的函数，即

1.2 跨层传输优化问题表达

所有SVC 视频需要从源节点经过多跳无线链路传送到sink 节点上．分配给各个链路的传输速率必须能够承载(即大于或等于)经过它们的视频流的速率．本文采用多径路由，即允许视频流在所有可能的端到端路径上传输．定义一个N × L的节点-链路矩阵H，hnl= 1表示节点n 是链路l 的发射节点，而 hnl= −1表示节点n 是链路l 的接收节点，否则 hnl= 0．定义=[ r1,…,rN]T为所有节点的源速率矢量，其中rn= 0,n ∉ S．在多径路由的网络中，流出某个节点的数据速率与流入的数据速率之差必须大于该节点的源速率[10]，即网络流必须满足如下条件：

在无线多跳网络中传输视频信息，总是希望用最小的传输功率获得尽可能好的视频质量．然而，这2个指标不可能同时满足，二者之间需要权衡考虑．为了在优化中体现这种权衡，本文采用如下的优化目标：γTQ - ηTP，其中，γ 和η 分别是sink 节点接收到的SVC 视频质量和无线链路功率消耗的加权系数矢量，它们的值代表2 个优化参数的重要程度．可以把η 看作是功率的 “成本”，而γ 为接收相应SVC 视频质量所获得的“收益”，因此，SVC 视频在无线多跳网络中传输的跨层权衡优化问题可以表述为

由于SVC 视频的率失真函数和链路速率函数都是凸函数，因此问题(5)是凸优化问题，可以采用经典的非线性优化算法(如内点法)来求解[11]．然而，这些集中式的算法要求网络配置计算性能强大的计算节点，并在优化之前需要所有节点把各自SVC 视频信息、所有链路的信道状态以及功率配置发送到该节点，而优化结果也需要向全网分发，这种机制会产生大量的控制消息，大大降低了无线多跳网络的运行效率和可扩展性．分布式算法是无线多跳网络多媒体承载迈向实际应用的关键．

2 问题求解和分布式算法

通过对约束条件(1)和(4)引入拉格朗日乘子μ= [μ1, …,μN]T和λ= [λ1, …,λN]T，可以获得问题(5)的拉格朗日函数为

记

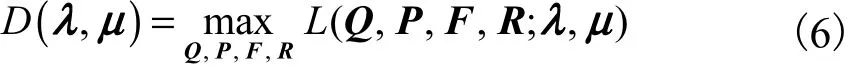
则问题(5)的对偶问题可以表示为

这里，λ和μ变成了对偶问题的优化变量．由于问题(5)是凸优化问题，因此可以通过求解其对偶问题(7)获得原问题的最优解(即对偶间隔为0)[12]．然而，虽然问题(7)是一个凸优化问题，但其目标函数却不是严格可微分的函数．这时可以通过次梯度(subgradient)法来搜寻其最优解[12]．假设在第i 步循环中对偶变量为λ(i)和μ(i)，求解式(6)中的最大化问题，获得最优的原变量 F∗、和W∗，则第i＋1 步的对偶变量按照如下方式更新，即

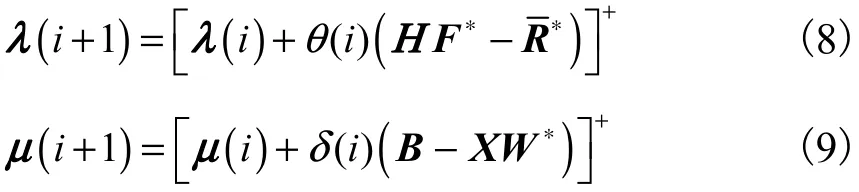
式中ΗF∗−和B −ΧW∗分别是函数 D(λ ,μ)在λ(i)和μ(i)处的次梯度．

在每一步更新对偶变量时，需要首先对对偶目标函数(6)中的最大化问题求解．对于给定的对偶变量λ(i)和μ(i)，该最大化问题可以分解为如下2 个独立的子问题：

问题(10)是SVC 视频流传输策略选择问题．对于给定的γ 和λ ，各个SVC 视频源传输策略选择相互独立．因此，问题(10)可以进一步分解为M 个独立的子问题，即

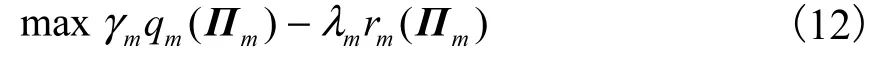
每个子问题可以在对应的SVC 视频源节点独立求解．每个源节点根据帧之间的预测关系和增强层的重要程度为每一帧选择相应的MGS 层，即Πm，使式(12)取得最大值．本文采用基于MGS-temporal 层的选择策略[2]．这种策略同时考虑帧所在的时序增强层和每帧中MGS 层的重要程度．由于帧所在的时序增强层越高对视频质量贡献越低，而每帧中MGS 层越高也对视频质量贡献越低，因此基于MGS-temporal层的选择策略在确定 Πm时，按照如下顺序选择SVC视频的传输内容：较低时序层的低MGS 层、较低时序层的高MGS 层、较高时序层的低MGS 层、较高时序层的高MGS 层，直到γmqm(Πm) −λmrm(Πm)取得最大值．采用这种选择策略，式(12)的目标函数是Πm的凸函数，因此对于确定的λm和γm总能找到最大值.

问题(11)是网络层资源分配问题，可以进一步分解为每个链路上的资源分配子问题，即

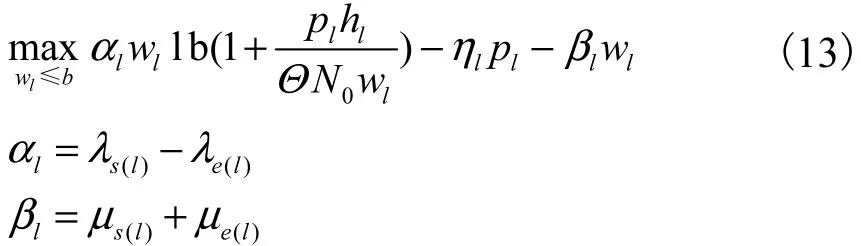
由于问题(13)不是变量 lw 和 lp 的严格凸函数，为了容易求解，本文采用文献[13]的方法在式(13)的目标函数中减去一个很小的正则化项(regularization term)ε，即

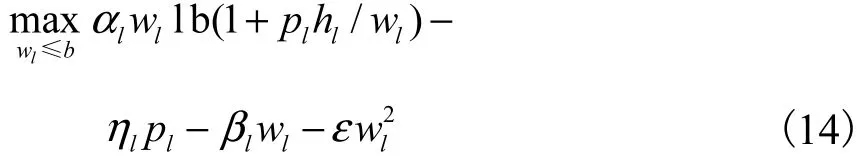
如果0ε→，则正则化后的最大化问题(14)的最优解趋近于问题(13)的最优解．正则化后很容易求得每个链路子问题(14)的解为

由上述求解过程可以得到无线多跳网络SVC 视频流传输的分布式跨层优化算法．

初始化根据网络应用要求和运营策略等确定权值γ 和η；设置对偶矢量λ(0)和 µ (0)各个分量的初值，并保存在相应的节点中；设置常量ε、固定步长θ和δ；告知各节点网络可用频带带宽b；发射节点测量并保存链路的信道增益 hl．

算法循环在第i 步执行下述操作：

(1) 每个节点n 向邻居节点广播对偶变量λn(i)和μn(i)；计算链路l 的发射节点的αl和βl值；

(2) 每个SVC 视频源节点m 采用基于MGStemporal层的选择策略确定 Πm，使式(12) 中

(3) 每个链路的发射节点根据式(15)和式(16)为该链路分配功率和带宽；

(4) 每个节点根据式(8)和式(9)更新其对应的对偶变量．

上述过程循环执行，直到收敛．

网络各节点和链路根据上述计算结果传输SVC视频信息．

可以看出，上述算法是通过网络中所有节点协同工作，以达到问题(5)的最优解．算法只需要在相邻节点间交换对偶变量，而各节点根据各自SVC 视频特点或链路状态独立地对相应子问题进行求解．分布式算法避免了集中式算法在全网传播控制信息和状态信息的问题．同时，该分布式优化算法实际上是对偶问题(7)的次梯度算法的应用．由于原问题(5)是凸优化问题，在得到问题(7)最优解的同时，也获得了原问题优化变量的最优值．另外，该算法同时分配底层资源、确定无线链路上的流速率和上层SVC 视频的传输内容，使之达到最优匹配．因此，所提出的无线多跳网络SVC 视频传输算法是一个分布式的、能够获得最优目标值的、跨层协同的SCV 视频流传输算法．

对于一个集中式算法来说，所有网络节点必须把所有算法相关信息发送到执行集中式计算的节点(如sink 节点)上并且这些信息可能需要多次转发．越接近sink 节点的转发节点所承载的控制信息越多．假设某个与sink 节点相邻的节点x 需要转发τM个SVC 源节点的信息和ζN个网络节点的信息(0 ≤τ,ζ≤1)．SVC 源节点的信息包括SVC 视频每个图像组(group of pictures)包含不同时间增强层和MGS 层的PSNR 值和数据量，假设这些参数总个数为A．可见如果SVC 视频较长，A 是非常大的．假设每个节点需要发送的信息的参数个数为B(这主要包括节点可用功率值、所有链路的发射距离、链路的连接和相互干扰情况)，则节点x 需要承载τMA +ζNB 个控制信息参数的转发．一方面这个值非常大，另一方面随着网络规模的增大、SVC 源节点数以及SVC 视频长度的增加，这个值也会快速增大．另外，集中式算法还要把最终计算结果进行全网分发，因而，集中式算法控制信息较高且可扩展性差．而本文所提出的分布式算法中，控制信息只在相邻节点之间传递，而且每个循环中，节点n 只有需向其所有邻节点一次性广播2 个参数λn和μn．假设算法循环次数为I ，每个节点需要广播2I 个信息．一方面该算法能够快速收敛，因而每个节点需要发送的参数个数远小于上述集中式算法．另一方面，该值与网络规模和拓扑、SVC源节点数、SVC 视频长度、数据流发送路径等均无关，因而具有很好的可扩展性．

3 仿真结果与分析

3.1 仿真场景与参数

本文采用如图1 所示的无线多跳网络拓扑验证所提出的算法性能．该拓扑包含16 个无线节点，均匀分布在150,m×150,m 的区域内．设置节点1、4 和13 为SVC 视频源节点，而右上角的节点16 为汇聚(sink) 节点．本文采用典型视频“silence of the lambs”、“NBC news” 和“sony demo” 分别作为3 个源节点所需发送的视频．这3 个视频的SVC-MGS 编码的trace 文件可以从网站[14]下载．设网络可用带宽为b＝200,kHz，设 hl/ΘN0=K，其中常数 K = 2 ×1 010，dl为链路l 发射和接收节点的距离(单位为m) ．

图1 仿真拓扑Fig.1 Topology for the simulations

为了在数值仿真中减少式(14)中正则化项的影响，需要对带宽和速率进行归一化处理，即b′=b/(2×105)，W′=W/(2 ×105)，R′= R/(2 ×105)和=/(2 ×105)，而常数变为K=105，但功率和PSNR 值不变．设ε=0.05．对偶变量的初值设置为1．步长θ=0.01，δ=0.005．

3.2 算法的收敛性

为了方便仿真结果显示，设加权矢量γ和η的各自分量相等，且γm/ηl=φ．在每次优化中比值φ是一个给定的常数．图2 显示了φ=3时SVC 视频的平均PSNR、网络总功率消耗以及链路(7，11)所分配的带宽随着循环次数的变化情况．可见，采用所提出的分布式算法，上述优化变量可以在300 多次循环后逐步收敛到稳定值，即平均PSNR 为37.018,dB，总功率消耗为2.253,W，链路(7，11)所分配带宽为63.46,,kHz．这说明所提出的分布式算法能够快速收敛，而由第2节分析可知收敛所达到的稳定值即是问题(5)的最优值．快速收敛的分布式协议能够减少无线多跳网络的控制信息交换开销和流传输的启动延迟．

图2 算法收敛性Fig.2 Convergence of the algorithm

3.3 不同加权比值下的优化结果

所提出算法在不同加权值比值φ的优化结果如图3 所示．本文的SVC 视频传输算法是“内容感知(content-aware)”的，即根据SVC 视频内容的重要程度确定是否发送．这可以与非内容感知(contentblind)的机制比较[15]，该机制以源速率效用函数(本文采用lnmr)最大化为优化目标，其优化结果如图3中的 “基于速率的优化”(注意基于速率的优化其底层资源分配仍然采用第2 节的方法) ．

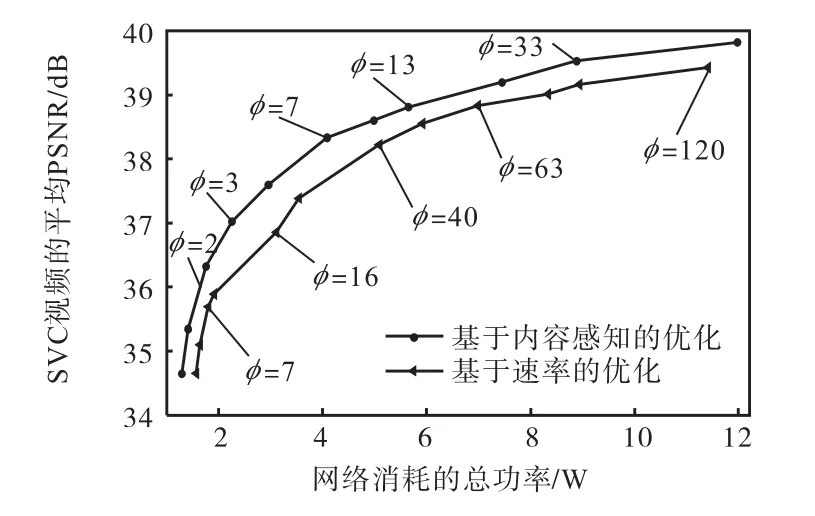
图3 优化结果与比较Fig.3 Optimization results and comparison

图3中每一点对应一个确定φ值的平均PSNR和功率消耗最佳权衡值(trade-off)．增大φ值相当于提高了式(5)中SVC 视频质量的权值或降低了功率的“成本”，因此优化算法可以分配更多的功率以提高传输视频的质量．相反，降低φ值相当于提高了功率成本，算法相应地降低SVC 视频的传输质量以节省无线多跳网络的功率和提高网络有效运行时间．实际φ值(或加权矢量γ和η)的设置依赖于具体的应用和网络管理策略．另一方面，采用本文的优化框架和底层资源分配机制，基于速率的优化结果与基于内容感知的优化具有相似的趋势．但由于不考虑SVC视频内容对PSNR 影响的差异，而直接对其速率效用函数进行优化，其优化性能明显低于内容感知的机制．从图3 可以看出，基于速率的优化在相同的功率消耗下，所获得的平均视频质量要低于基于内容感知的机制，或者说要得到相同的平均视频质量，需要消耗更多的网络功率．

4 结 语

本文提出了一种无线多跳网络中SVC 视频流的分布式传输优化算法．该算法是基于非线性优化中的对偶理论，用次梯度算法对传输质量和功率消耗的跨层权衡优化问题的对偶问题进行求解的过程中推导出来的．分布式算法把问题分解为可以在对应无线节点上独立求解的带宽和功率分配子问题以及SVC视频内容选择子问题，通过节点的本地信息交换和在网协同工作，获得相关优化参数的最优值，避免了控制信息的集中式收集和全网分发．本文所提出的算法能够为无线多跳网络的设计和实际部署提供参考依据．

本文所提出的算法中传输质量和功率的加权系数比值决定了SVC 视频流传输和网络功率消耗的最优权衡点．今后将进一步研究这些参数与无线多跳网络的能量管理策略、有效运行时间以及多媒体的服务质量保证等的相互关系和影响．

［1］Schwarz H，Marpe D，Wiegand T. Overview of the scalable video coding extension of the H.264/AVC standard[J]. IEEE Transactions on Circuits and Systems for Video Technology，2007，17(9)：1103-1120.

［2］Seeling P，Reisslein M. Video transport evaluation with H.264 video traces[J]. IEEE Communications Surveys and Tutorials，2011，14(4)：1142-1165.

［3］Pourmohammadi-Fallah Y，Mansour H，Khan S，et al.A link adaptation technique for efficient transmission of H.264 scalable video over multirate WLANs[J]. IEEE Transactions on Circuits and Systems for Video Technology，2008，18(7)：875-887.

［4］Mansour H，Fallah Y P，Nasiopoulos P，et al. Dynamic resource allocation for MGS H.264/AVC video transmission over link-adaptive networks[J]. IEEE Transactions on Multimedia ， 2009 ， 11(8)： 1478-1491.

［5］Zhang Honghai ， Zheng Yanyan ， Khojastepour Mohammad A，et al. Scalable video streaming over fading wireless channels[C]// IEEE Wireless Communications and Networking Conference. Budapest，Hungary，2009：1-6.

［6］孙刚友. 无线网络中H.264/SVC 视频传输的QoS 保障机制[J]. 电信快报：网络与通信，2011，26(7)：41-44.Sun Gangyou. QoS guarantee mechanism for H.264/SVC video transmission[J]. Telecommunication Information：Network and Communication，2011，26(7)：41-44(in Chinese).

［7］Akyildiz I F，Wang Xudong，Wang Weilin. Wireless mesh networks：A survey [J]. Computer Networks，2005，47(4)：445-487.

［8］Yick J，Mukherjee B，Ghosal D. Wireless sensor network survey[J]. Computer Networks，2008，52(12)：2292-2330.

［9］由 磊. 无线多跳网络跨层设计与优化的相关理论和算法研究[D]. 北京：北京邮电大学电子工程学院，2009.You Lei. Research on the Theory and Algorithms of Cross-Layer Design and Optimization for Wireless Multihop Network[D]. Beijing：School of Electronic Engineering，Beijing University of Posts and Telecommunications，2009(in Chinese).

［10］Lin Xiaojun，Shroff N B. The impact of imperfect scheduling on cross-layer rate control in multi-hop wireless networks [C]//IEEE International Conference on Computer Communications. Miami，Florida，USA，2005：1804-1814.

［11］Bertsekas D P. Nonlinear Programming[M]. Belmont，MA：Athena Scientific，1999.

［12］Boyd S，Xiao L，Mutapcic A. Subgradient Methods[EB/OL]. http ： //trace.eas.asu.edu/videotraces2/mgs/index.php，2012-01-06.

［13］Bertsekas D P，Tsitsiklis J N. Parallel and Distributed Computation ： Numerical Methods[M]. Belmont ，MA，USA：Athena Scientific，1997.

［14］Reisslein M，Karam L J，Seeling P，et al. Video Traces for Network Performance Evaluation[EB/OL]. http：//trace. eas. asu. edu/videotraces2/mgs/index. php，2012-01-06.

［15］Palomar D P，Chiang M. A tutorial on decomposition methods for network utility maximization[J]. IEEE Journal on Selected Areas in Communications，2006，24(8)：1439-1451.