Otto结构加载MIM波导的表面等离子激元传输与衰减特性
朱 君,李志全
(燕山大学电气工程学院检测技术与自动化装置,河北秦皇岛 066004)
1 引 言
早在1950年,表面等离子激元(Surface Plasmon Polaritons,SPPs)就被人们所认识,其本质上被定义为横向电磁场和金属表面自由电子相互作用的一种电磁场模式,或者是自由电子和光波电磁场由于共振频率相同而形成的一种集体振荡态[1]。SPPs在光纳米电路中表现为谐振、场放大、局域以及亚波长的限制等一系列有意义性质,已应用到光谱仪、纳米光学、成像技术和生物传感等多个方面[2-8]。其中基于光学纳米电路表面等离子(SP)中更低损耗的亚波长孔径MIM(金属-介质-金属)波导的探究,同样获得了很多有意义的发展。其中,Radko等[9]报道了在 Au上掺杂PMMA条纹的PbS量子点(QD)结构,预测SPP传播长度可以增加32%。Chen等模拟了Au-InGaAs-Au结构,得出了75 nm厚的这一结构中无损SPP传播和纳米环形激光器的性能。Grandidier等[10]研究了银膜掺杂PMMA条纹,分析推论了SPPs的传播特性。然而,尽管SPPs具有满足Maxwell方程、玻色一般规则(SPPs是玻色子)以及可以实现能量量子化等特性,但在MIM波导结构中限制SPPs小范围内传播的性质一直未有统一的认识和应用[11-15];同时,结构表面材料粗糙度对SPPs传播特性的影响,也一直未达成共性认识[16-20]。本文基于这一背景,研究了加载MIM结构的Otto装置的SPPs激射传输特性,分析了不同介质厚度下的衰减,最后仿真比较了归一化介质厚度的传播特性。这一研究对于SPPs的激射的进一步改进具有一定的意义。
2 MIM结构理论分析
2.1 SPPs的共振态
SPPs传播中存在的共振态指的是Maxwell方程的本征态,这与金属的组成材料(或表面深度)无关,产生的共振态场一旦激发,就会辐射电磁波到远场区,能量将消失变成内能(倏逝波)。这里先讨论一个理想介质源的本征值,结构以球形面进行分析。设介质为半径为a的球形面。利用Maxwell方程得这一球形的TE、TM模矢量关系:
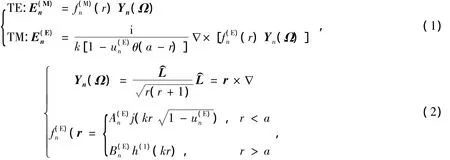
其中θ(r)是阶跃函数,n为系数,k是介电常数,j、h(1)分别是球面的 Bessel函数和 Hankel函数,是对应方程的一个特解。方程(1)存在无穷数列的解且特征值都是复数。如果a→0,则存在唯一的特征值是,此为准静态表面等离子共振态。
上述球面的EM场的解法推广到整个介质区域(半无限结构),可得系统的本征函数的特征值:

以上对本征态求解介质表面在SPPs传播形成中可得两条基本对称性质:z向的旋转对称—可确定离散系数;空间反演对称—即本征态的奇偶性。由对称特性可知,可以构建形成(和取消)奇(偶)同位的偶极子。
2.2 MIM结构理论分析
应用以上本征态的理论分析,结合MIM结构(图1)中TM波的边界条件,得这一结构的特征方程为:


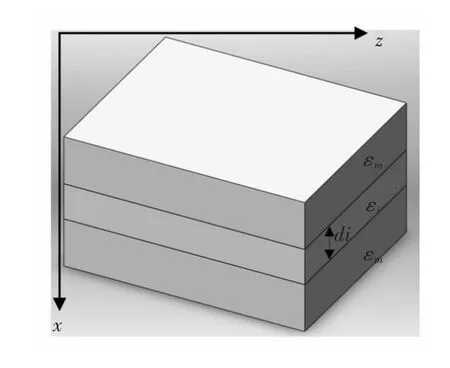
图1 MIM结构示意图Fig.1 Schematic diagram of MIM structure
分析上述腔内的入射耦合,有自由空间波长λ的H=0(0,Hy,0),透射到腔内的波矢这里定义为对称的间隙SPP,由Ez场的连续性可得:上式中t是前向传播对称SPP电场Espz幅值,其可定义为SPP的激发系数;Erefz为反射场。进一步分析,在幅值g(k)为连续平面波模式中,方程(2)则能变化为:

这样就得到了场的连续方程,下一步依据边界条件计算SPP激发系数t。这里定义的边界条件是在腔终端通过yz平面的x方向能流通量是连续的。在y方向上由于系统坐标是不变的,这样在z方向上有:

上述公式中的“*”表示值的共轭复值。应用方程(3)简化方程(5)求解t,可得下面的表达式求解SPP传播系数:
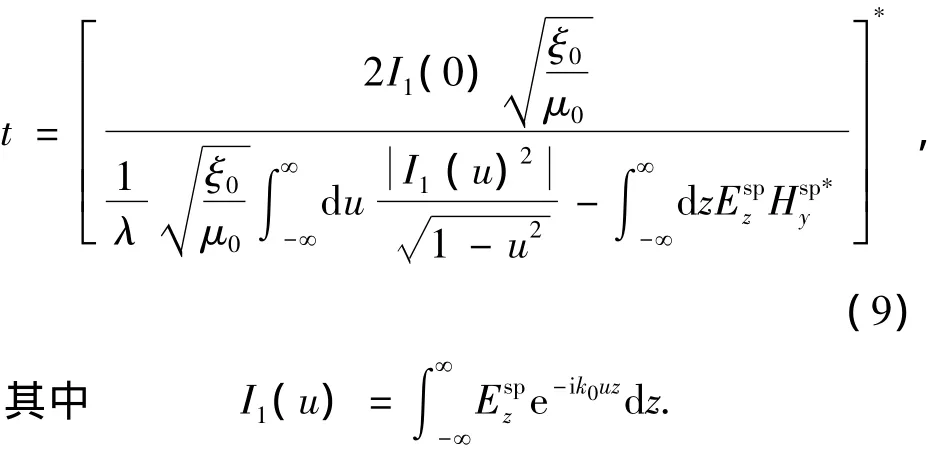
2.3 模型的传输分析
本文设计采用如图2所示Otto和MIM结构结合的模型,应用横向传播/反射(TTR)的方法,完成MIM等离子模式的失真的简化。这一结构可实现入射光通过波导截面的改进,其横向激发就是一个等离子模式。

图2 ATR装置应用的一个对称的MIM结构Fig.2 ATR apparatus application of a symmetrical structure of the MIM structure
应用MIM结构的Maxwell电磁场理论,上述结构的每层传输矩阵为:

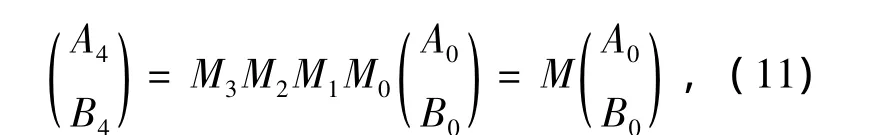
上式中对于 TE 波,fi=1;对于 TM 波,fi= ξi+1/ξi。di是第i层厚度。此外,对任一边界的场幅值可由矩阵方程得:其中A和B是对应于相应界面的+x和-x传播波场的幅值(对于TE波是Ey,对于TM波是Hy)。此外由加载MIM结构棱镜的特性,其传输矩阵还可表示为:

上式在MIM结构中,当m22=0时为相应的波导模式。由MIM结构的结构反射系数可得这一结构的反射系数为:

3 模型分析
3.1 传播常数β/k0和衰减系数∂/k0的分析
基于以上的理论分析,在进行模型分析前首先进行以下简化:假设腔内存在的倏逝模式和腔边界表面横向传播(z方向)SPP模式一样连续,耦合面透射系数是在金属有一个很大负介电常数情况下得到的,模型验证选定为加载Au-SiO2-Au波导的Otto结构。这里对波长λ=1 550 nm,SiO2厚度分别为di=750 nm和1 500 nm的改进结构进行分析。为了实现近似耦合强度,上端的Au层选择为80 nm厚(约为3层趋肤深度),底层Au介质为420 nm(相当于采用半无限分析),且有在λ=1 550 nm 时,Au的折射系数是0.526 -j10.74;对于厚度 di=750 nm,1 500 nm,nSiO2=1.487 7,1.468。
基于上述条件与建设,表1给出了相对传播常数β/k0和相对衰减系数∂/k0的相应模式的理论计算结果。从表中可知,所以模式都存在着衰减系数减小的趋势,在1 500 nm的结构中,TE0模式的衰减最低。比较两种厚度结构的传播与衰减结果,采用750 nm的结构的TM0传播常数达到了1.541,衰减系数只有2.80,这一结果对于SPPs在多模MIM波导传输距离的研究具有一定的借鉴价值。

表1 传播常数β/k0和衰减系数∂/k0Table 1 Propagation constant β/k0and the extinction coefficient∂/k0
3.2 归一化仿真分析
为了进一步分析厚度的影响,图3给出了不同金属介电常数的归一化厚度的波长反射系数与相位的关系。由图可知,反射系数随着SiO2介质厚度的减小而增大,且不同金属介电常数谐振方向变化趋势一致。这一结果可用来实现设计模型传输距离的控制即SPPs激射控制,即通过控制归一化厚度实现耦合有效性以及衰减控制。这一结果与表1的传输常数Δ∂/k0以及模式理论分析结果显然是对应的。
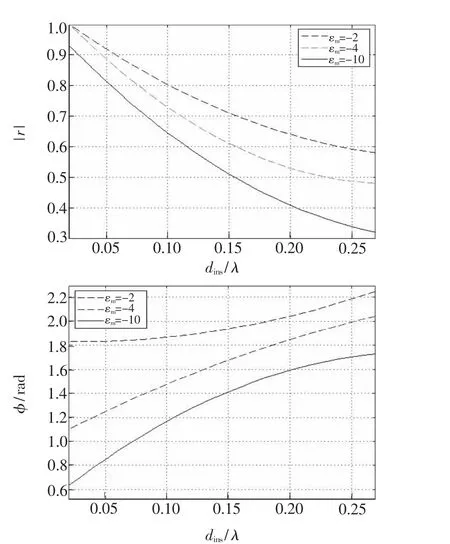
图3 不同ξm 值下的r 和φ(相位)与SiO2厚度的关系Fig.3 Relationship of r and φ(phase)vs.normalized SiO2thickness dins/λ under different ξm
4 结 论
传播SPPs的光学结构和器件为在纳米尺度上操控光子,完成全光集成,发展更小、更高效的纳米光子学器件提供了一条有效的途径。SPPs一直未产生较明显的实际应用价值就是由过高损耗造成的。文中研究的加载波导的Otto结构,在给出设计结构的同时着重分析了这一结构的传输损耗问题,结果发现采用750 nm介质厚度的结构的TM0传播常数达到了1.541,衰减系数为2.80,这一损耗结果对于SPPs激射的进一步改进具有一定的借鉴价值。
[1]Ritchie R H.Plasma losses by fast electrons in thin films[J].Phys.Rev.,1957,106(5):874-881.
[2]Wang Y L,Shi Y S,Hou B H,et al.THz and infrared absorption spectra of Zn3BPO7crystal[J].J.Synth.Cryst.2010,39(4):838-841.
[3]Walters R J,Van Loon R V A,Brunets I,et al.A silicon-based electrical source of surface plasmon polaritons[J].Nat.Mater.,20010,9(1):21-25.
[4]Gao G Y.The study of coherence of surface plasmon polaritons[D].Tianjin:Nankai University,2010.
[5]Ge Y J,Zhang G Q,Chen Q.Plasma Science Technology and Its Application in Industry[M].Beijing:China Light Industry Press,2007.
[6]Wood J J,Tomlinson L A,Hess O,et al.Spoof plasmon polaritons in slanted geometries[J].Phys.Rev.B,2012,85(7):075441-1-7.
[7]Cuche A,Mahboub O,Devaux E,et al.Plasmonic coherent drive of an optical trap[J].Phys.Rev.Lett.,2012,108(2):026801-1-4.
[8]Zeng X D,Xu J P,Yang Y P.Spontaneous emission interference enhancement with a μ-negative metamaterial slab[J].Phys.Rev.A ,2011,84(3):033834-1-5.
[9]Huang D X,Liu X F.Semiconductor Laser and Applications[M].Beijing:National Defence Undustry Press,1999.
[10]Stockman M I.The spaser nanoscale quantum generator and ultrafast amplifier[J].J.Opt.,2010,12(2):024004-1-13.
[11]Stockman M I.Spaser action,loss compensation,and stability in plasmonic systems with gain [J].Phys.Rev.Lett.,2011,106(15):156802-1-4.
[12]Li N,Ni X C,Wang B.Research progress of surface plasmon polaritons[J].J.Tianjin Univ.Technol.Edu.(天津职业技术师范学院学报),2010,20(4):18-23(in Chinese).
[14]Shepherd H J,Bonnet S,Guionneau P,et al.Pressure-induced two-step spin transition with structural symmetry breaking:X-ray diffraction,magnetic,and Raman studies[J].Phys.Rev.B,2011,84(14):144107-1-5.
[16]Noginov M A,Zhu G,Belgrave A M,et al.Demonstration of a spaser-based nanolaser[J].Nature,2009,460:1110-1112.
[17]Stockman M I,Brongersma L,Shalaev V M.The case for plasmonics[J].Science,2010,1126:440-441.
[18]Wiersma D S,Noginov M A.Nano and random lasers[J].J.Opt.,2010,12(2):020201-1-3.
[19]Fang Z Y,Peng Q,Song W T,et al.Focusing in symmetry broken nanocorrals[J].Nano Lett.,2011,11(2):893-897.
[20]Fedotov V A,Papasimakis N,Plum E,et al.Spectral collapse in ensembles of metamolecules[J].Phys.Rev.Lett.,2010,104(22):223901-1-3.

