基于四阶Runge-Kutta方法的大地主题正算*

朱宁宁，张赵兴，梁晓莉，魏祖帅

(河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室，河南焦作454003)

椭球面上点的大地经度、大地纬度，两点间的大地线长度及其正、反大地方位角，统称为大地元素。通过已知的某些大地元素推求另一些大地元素，这样的计算称为大地主题解算。大地主题解算是大地主题正算和反算的统称，是椭球面大地测量学研究的核心问题之一［1］。

大地主题解算常用的一种方法是运用勒让德级数将它们展开为大地线长度的升幂级数，再逐项计算以达到主题解算的目的。但是这种级数式收敛缓慢，项目繁多，计算起来非常复杂，虽然经过不同学者的改进，可以达到精度很高的解算值，但该方法涉及的数学技巧多，要求掌握较多的椭球大地测量和空间解析几何知识［1-2］。计算机的发展和数值计算算法的提高，为一些原本封闭的方程和偏微分方程等在传统手工方法下难以解算的问题，提供了数值方法的解算途径［3-4］。这些问题的数值解可以人为控制精度，并以很快的速度进行解算。对于数值计算方法，目前文献主要讨论的是数值积分法，而在此类问题中，应用微分方程的数值解法进行求解在目前的文献中尚不多见。本文提出一种用四阶Runge-Kutta方法求解大地线微分方程的数值解法，该方法通过椭球面上各大地元素之间的严密函数关系，导出了椭球面上的大地线微分方程组计算模型，并用四阶Runge-Kutta方法求解经过组合后的微分方程组，完成了大地主题正算。

1 四阶Runge-Kutta方法的分析及模型

1.1 龙格-库塔(Runge-Kutta)法解大地线微分方程分析

龙格-库塔(Runge-Kutta)法解大地线微分方程的实质是用若干点函数值的线性组合来代替泰勒级数展开式中的导数计算。四阶Runge-Kutta方法属于数值积分算法，它既不采用勒让德级数也不用借用辅助面。使用这种方法可以达到较高的解算精度，可用于解算150 km以内的大地主题正解。该算法简单、易于编程，并且可以达到和经典的高斯平均引数法相当的计算量。

1.2 大地线微分方程

椭球参数计算示意图如图1所示，设P为大地线上任意一点，其经度为L，纬度为B，大地线方位角为A。当大地线增加dS到点P1时，则上述各量相应变化dL、dB及dA。大地线的微分方程可表达为dL、dB、dA与dS的关系式。由图1可知，dS在子午圈上的分量P2P1=M·dB，在平行圈上的分量PP2=N·cosB·dL。三角形PP2P1是个一微分直角三角形，它结合球面直角三角形P1P3N，可求得大地线微分方程组中dL、dB、dA与dS的关系式:

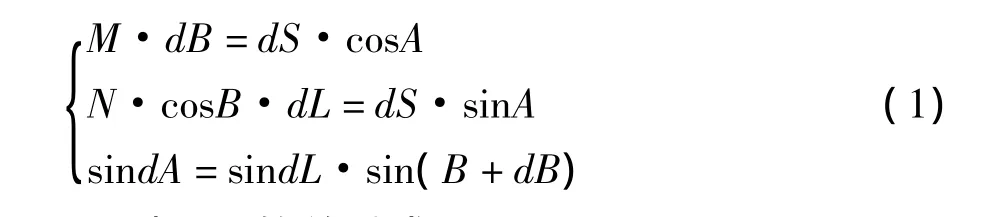
将式(1)化为dL、dB、dA与dS的关系式:

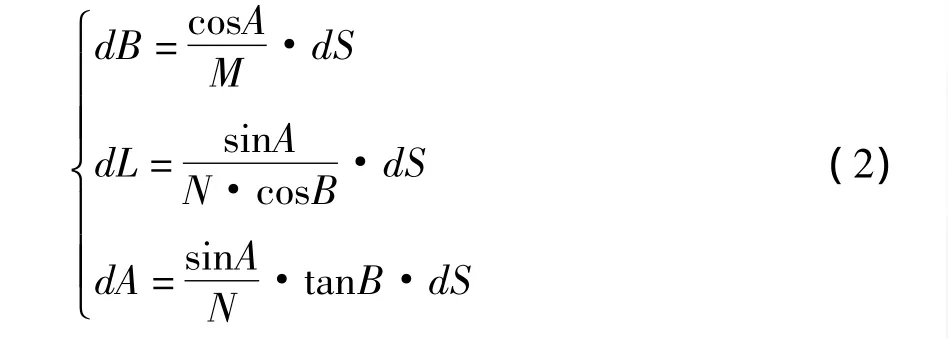
式(2)称为大地线微分方程，是本文所用四阶龙格 －库塔(Runge-Kutta)法的基本函数模型。

图1 椭球参数计算示意图

1.3 四阶Runge-Kutta模型

Runge-Kutta方法实质上是间接地使用Taylor级数法的一种方法。考虑差商，根据微分中值定理，存在0＜θ＜1，使得

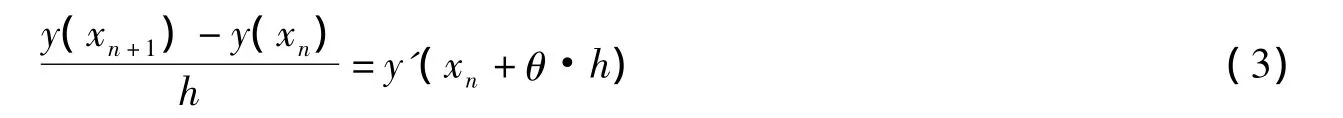
于是，利用所给方程y'=f(x，y)得到

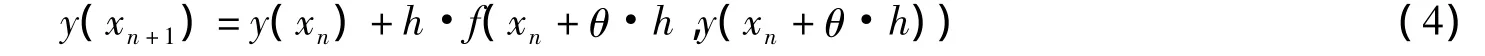
设K*=f(xn+θ·h，y(xn+θ·h))，称K*为区间［xn，xn+1］上的平均斜率。由此可见，精确求解微分方程数值解的关键是找到一个适当的平均斜率。采用四阶Runge-Kutta方法确定的平均斜率，可使求解值具有四阶精度，即局部截断误差是O(h5)。具体做法是在区间［xn，xn+1］上用四个点处的斜率加权作为平均斜率的近似值。四阶Runge-Kutta具有多种格式，本文采用经典格式模型［5］。

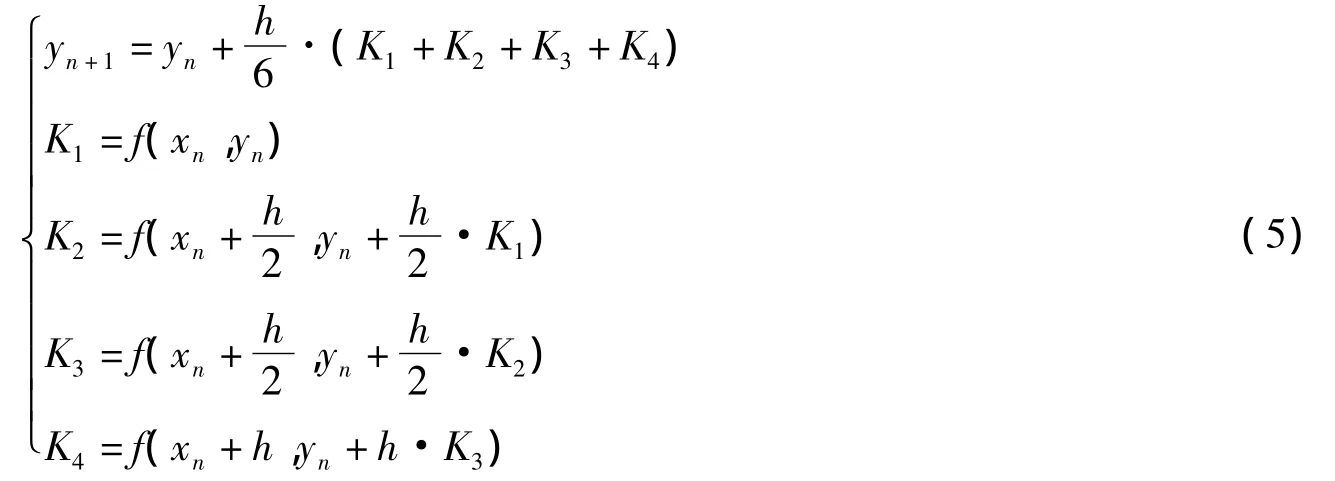
1.4 四阶Runge-Kutta法求解大地线微分方程

大地线微分方程中分别包含dL、dB、dA与dS的关系式，各个变量之间具有相关性，经典格式只包含单一方程，为将其用于解算大地元素，需将经典格式改写为方程组形式，得到求解模型。

大地主题正解微分方程组可表示为:

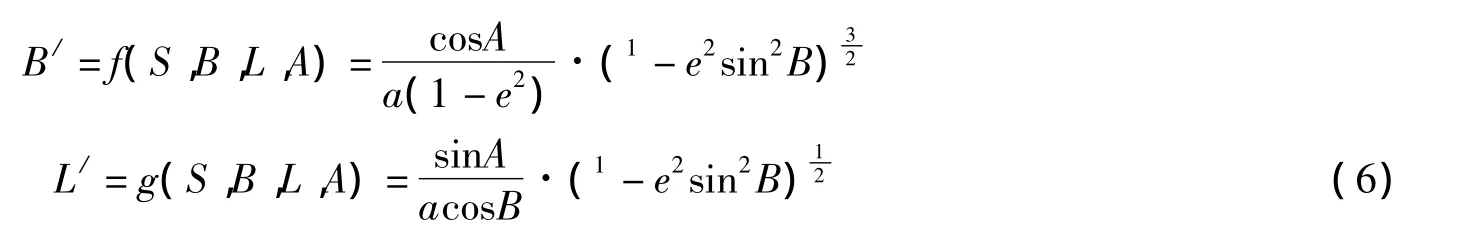
改进的四阶Runge-Kutta经典形式为:

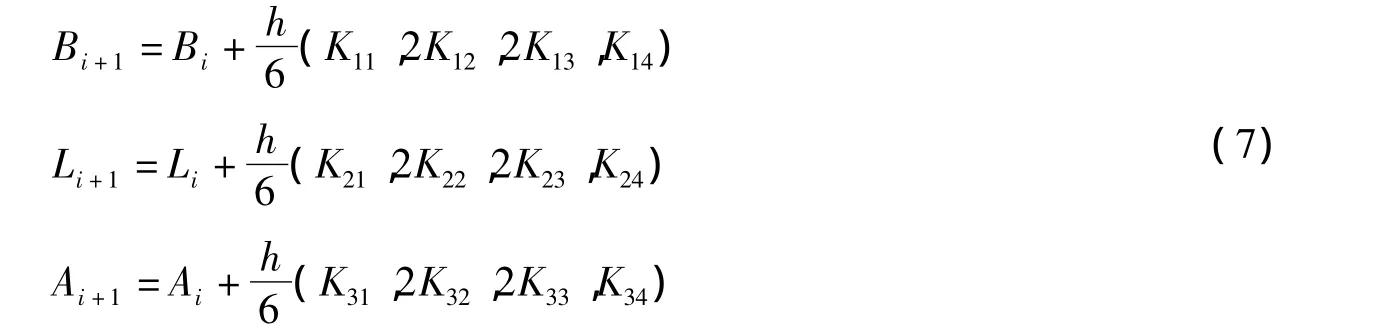
大地主题正算的初始条件为 B0、L0、A0、S，则有

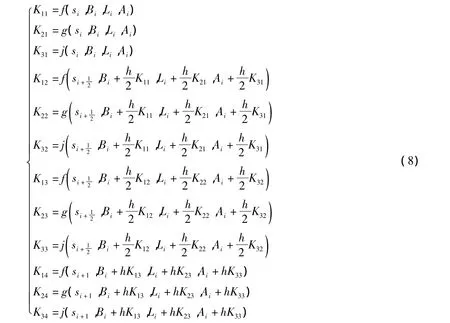
式中:h为等分后步长;si为选取的大地线的第i个等分节点到起始点的大地线长度。

由此可以看出，用改进的经典四阶Runge-Kutta法进行大地主题的正算，公式简洁、规律明显、易于理解，而且易于编程实现。

2 算例分析

本文使用C++编程，实现上述算法，在克拉索夫斯基椭球上进行计算，椭球的参数为长半轴a=6 378 245.0 m，椭球第一偏心率为e，e2=0.006 693 421 622 966，将经典算法的解算值作为参考值，比较本文算法与经典算法的差别。表1的四个例子中大地线S等分的个数分别选为10、10、100、100.

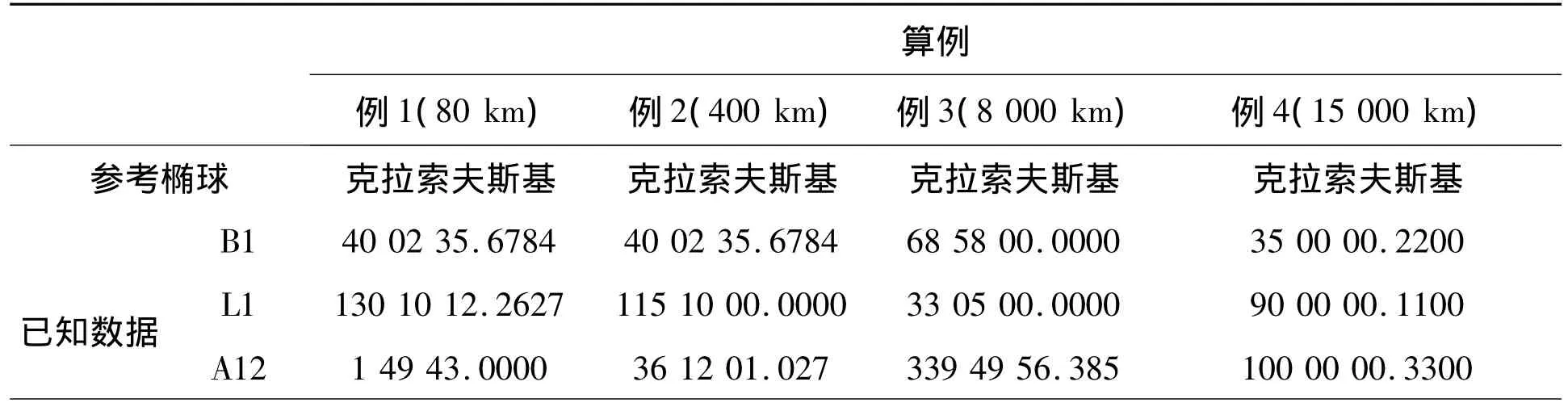
表1 大地主题正解解算结果 °'″

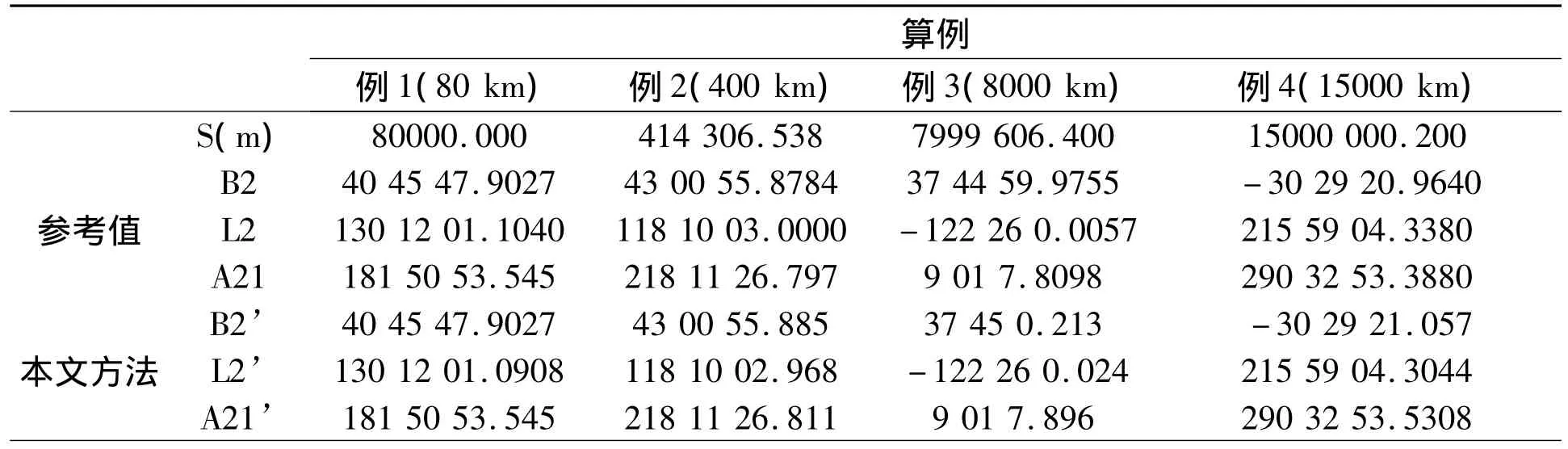
续表

表1算例包含了短距离(例1)，中距离(例2)，长距离(例3、4)等情况，最大的偏差在例3中B2-B2’的解算中，有亚秒级的差别，其余的差别大多在毫秒级别上，分析偏差的原因，主要有两项，一是距离的影响，二是等分节点个数的选择。当距离一定时，合理的选择节点可以很大程度上提高精度。因此，若需提高精度，简单的方法是仅增加等分节点的个数，不需要改变程序的其它部分。这与经典的基于级数展开的算法有很大不同，经典算法如果要提高精度，需要增加多项式展开的次数，这会导致求解公式变得复杂，程序也要作较大改动。

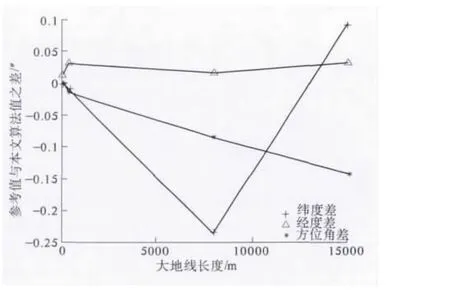
图2 解算结果比较图

3 结论

本文提出的大地主题正解的数值解法，采用严密公式进行计算，而且公式表达简单，特别适合计算机计算。本文对正解的微分方程采用单步的龙格－库塔方法进行解算。理论上，如果采用多步法，如Adams方法，那么对于作为光滑曲线的大地线来说将可以得到任意精度的解算结果。

［1］ 孔祥元，郭际明，刘宗全.大地测量学基础［M］.武汉:武汉大学出版社，2002.

［2］ 周振宇，郭广礼，贾新果.大地主题解算方法综述［J］.测绘科学，2007(4):190－191.

［3］ 王建强，胡明庆.贝赛尔大地主题解算分析［J］.测绘科学，2012(1):30－31.

［4］ 范业明，王解先，刘慧芹.大地主题的数值解法［J］.工程勘察，2007，38(1):6－9.

［5］ 李庆扬，王能超，易大义.数值分析［M］.武汉:华中科技大学出版社，2006.