利用常规测井资料识别裂缝方法研究

董双波，柯式镇，张红静，刘春艳

（1.承德石油高等专科学校石油工程系，河北 承德067060；2.中国石油大学地球物理与信息工程学院，北京102249）

0 引 言

随着石油天然气勘探的不断深入，裂缝性储集体逐渐成为勘探的重点。对于裂缝性储集体的地球物理探测主要是通过采用先进的成像测井技术完成［1－2］，由于成像测井的成本非常高，其普及率受到限制，大部分油气田的测井资料还是以常规测井资料为主，因而在没有成像测井资料的情况下利用常规测井资料有效地识别裂缝的技术非常重要。利用常规测井资料识别裂缝的方法在国内外已经开展了大量研究［3－23］，这些研究较多是针对某种特定地质条件下的方法［3，7，10－11，19－20，22］或针对有限的几种测井方法［4－6，8－9，12－18，23］，综合程度不够高，而且在这些文献中鲜见对不同裂缝识别方法进行对比分析。

本文通过借鉴前人的研究成果，将多种方法综合起来，形成综合了多达24个特征参数的加权概率指数识别裂缝的方法；将其与小波变换法和分形维数法进行了实际资料处理对比分析，给出了对比结论；将这3种算法形成了软件，为工程应用提供了工具。

1 裂缝识别方法原理

各种常规测井对裂缝的反映都是微弱的，从机理上它们又都有反映。例如双侧向测井测得的深浅电阻率差异受地层裂缝的发育程度影响，对于裂缝发育层段，深、浅电阻率值明显减小而且幅度差增大。声波测井测得的时差在裂缝发育段会明显增大且容易出现周波跳跃现象。井径测井测得的井径曲线在裂缝发育井段会表现出激烈的震荡和扩径。自然伽马能谱测井曲线在裂缝发育段表现出U元素含量的增加。密度测井测得的岩石体积密度在裂缝发育段明显减小等。

常规测井曲线上裂缝的响应信号与反映地层变化情况的慢变信号相比具有较小的幅度和较高的变化频率，称之为高频微弱信号。利用常规测井资料识别裂缝的本质就是要从常规测井曲线上分离提取反映裂缝发育情况的高频微弱信号，并根据高频微弱信号的出现和明显情况识别裂缝发育井段。据此，原则上所有信号处理手段均可以用来解决常规测井资料识别裂缝的问题。在本文中，重点讨论了小波变换、分形维数和裂缝特征参数加权概率指数法这3类方法。

1.1 小波变换法

小波变换与傅里叶变换相似，它将信号分解为由一系列小波的组合，从而将时域信号变换到小波域。小波变换有正变换和逆变换2个过程，一般的信号处理过程是先将时域信号变换到小波域，然后在小波域对组合系数进行修改，最后再进行逆变换从而达到对信号的处理目的。小波变换根据小波函数的不同分成很多种，本文采用了Mallat小波基函数［22］，其快速算法为

正变换（分解）

逆变换（重建）

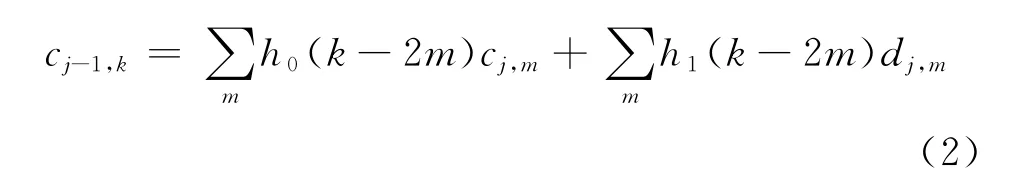
式中，h0、h1为由小波函数计算得到的系数，一般理解为滤波器系数；c和d为组合系数，c系数代表时域信号中低频成分的能量信息，d系数代表高频成分的能量信息。

将小波变换用于常规测井识别裂缝的实质就是通过小波分解、重构及反映低频和高频成分能量信息系数的修改，提取测井曲线中反映裂缝发育情况的高频微弱信号，从而识别裂缝发育层段。

1.2 分形维数法

分形几何学主要揭示了某事物部分与整体、微观与宏观的自相似性及其内在相关规律。分形几何学反映在不同尺度自相似结构的嵌套级次，并强调在一定范围内与尺度无关。分形分布的几何体以其间断离散为特征，而不是充满空间。这种特征可以用1个参数定量化，即分形维数。分形维数的大小反映1个几何对象的复杂程度，分形维数越大则说明所描述的几何对象越复杂。

对于常规测井曲线，其形态、幅值等特征上的复杂性或非均一性反映着地层特性的变化，它们也具有分形特性。对于致密地层，储层岩性、物性、含流体性质和裂缝孔隙空间结构越复杂，则其测井曲线高低起伏越大，左右摆动越剧烈，形状幅值相对异常越明显，曲线分形结构就越复杂，分形维数值就越大。

测井曲线分形维数的计算方法：将所研究储层段的测井曲线所在的平面逐次加密网格（实际上，测井图上的曲线都被绘在二维平面纸上，具有左右刻度和纵横向刻度分隔线，第1次网格化时，可以原图上的刻度分隔线作为网格线），如记曲线依次所穿过的网格数分别为N（L1），N（L2），…，N（Li），则网格数的统计公式［3］为

式中，n为该层段内曲线数据点数；Li为第i次网格加密后的网格数，1≤i≤j≤n；V为测井值，对于电阻率测井可为测井值的对数值。这些数据对存在统计关系

两边取对数则有

式中，D为分形维数；C为待定系数。用该方程去拟合前面不同网格数Li与曲线穿过网格次数N（Li）的数据系列，可以得到分形维数D。

1.3 加权概率指数法

根据各种测井方法本身的物理机理与裂缝的关系，可以提取对裂缝相对敏感的特征参数，形成裂缝特征参数曲线，然后根据该特征曲线识别裂缝。这样不同的常规测井曲线可以计算出不同的裂缝特征参数曲线。在实际应用中发现，利用单一的特征参数曲线识别裂缝其成功率很低，可靠性不高。为解决此问题，人们提出了将各种裂缝特征参数综合起来，合成一个可靠性较高的综合参数即加权概率指数，然后利用该参数进行裂缝识别。这种综合多个裂缝特征参数的识别裂缝方法被称为加权概率指数法。加权概率指数计算公式为

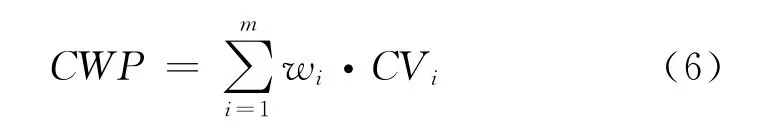
式中，CVi为第i种反映裂缝的特征参数值；wi为第i种反映裂缝特征参数值的加权系数，其值可以根据先验数据（如岩心观察）进行标定，也可以统一给定为1。

对裂缝敏感的特征参数提取是该方法的关键，裂缝特征参数越多，该方法识别裂缝的可靠性越高，裂缝发育层段的异常显示越明显，识别也越容易。本文提取了最多达24个的裂缝特征参数（见表1）。

表1 由常规测井资料提取的裂缝特征参数

（1）三孔隙度比值。由三孔隙度测井的测量原理知，中子测井和密度测井反映了地层总孔隙度的大小，声波速度测井主要反映原生的粒间孔隙度和水平裂缝。因此在裂缝性地层中，通过求得总孔隙度φt、中子孔隙度φN、密度孔隙度φD、声波孔隙度φS，可构造比值

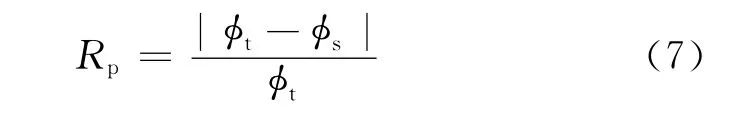
（2）电阻率侵入校正差比。定义电阻率侵入校正差比为

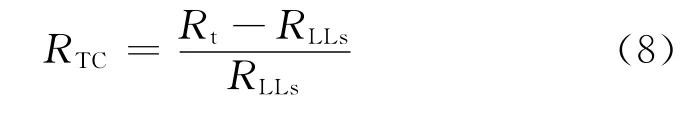
式中，Rt为经过侵入校正的地层真电阻率。

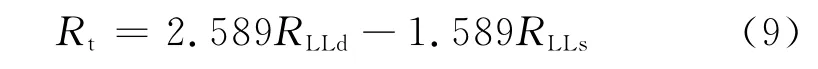
式中，RLLd、RLLs分别为深、浅侧向电阻率。

当地层为裂缝性油气层时，Rt＞RLLs、RTC＞0；当地层为裂缝性水层或致密地层时Rt≈RLLs、RTC≈0。该方法适用的条件是泥浆滤液沿裂缝侵入的深度在双侧向的探测范围内。

（3）龟裂系数。根据岩石纵波波速与岩石完整性的关系，对岩石裂缝敏感的龟裂系数为

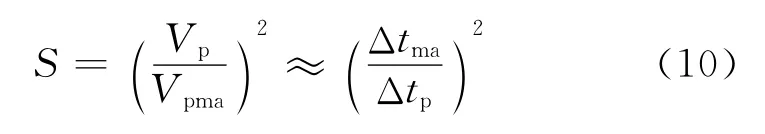
式中，Vp、Vpma分别为地层和岩石骨架的纵波速度；Δtma、Δtp分别为岩石骨架和地层的声波时差。S越大，岩石声波时差与岩石骨架声波时差越接近，说明岩石的完整性越好，裂缝发育间隙越大，裂缝发育频率越小；S越小，岩石破坏越严重，裂缝发育间隙越小，裂缝发育频率越大。因此，用龟裂系数来识别地层裂缝的发育程度。当裂缝发育时，S减小。

（4）井径相对异常。

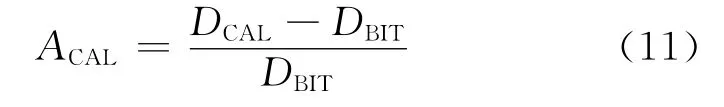
式中，DCAL为实测井径值；DBIT为钻头直径。ACAL值越高，表示井径扩径越大，地层越易破碎，对应储层的裂缝和孔洞发育的可能性越大。反之，ACAL值越低（或越趋于1），反映地层岩性较纯，对应地层为致密层或孔隙性储层的可能性越大。

其他的裂缝特征参数的构造与以上参数类似，它们的构造均从测井响应机理入手，重点考虑裂缝响应特征，从而起到突出反映裂缝响应的高频微弱信号的目的。在实际应用过程中，根据收集到的测井资料的情况可自动选择能够计算出来的所有特征参数参与综合，也可以人机交互选择，没有足够信息计算的参数自动无效。各特征参数的权系数在没有先验知识的情况下按平均权重设置，否则根据已有的正确信息经相关性分析给出不同的权系数。本文的处理实例是采用第1种情况设置得到的。

2 实际资料处理验证

根据上述原理，编制了小波变换、分形维数和加权概率指数这3种方法的常规测井资料识别裂缝的处理程序，并对某油田6口取心井的常规测井资料进行了处理和验证。图1是某井的处理结果，其中岩心道上涂黑处为岩心观察裂缝发育井段，WLTAC是对单条测井曲线（声波曲线）采用小波变换处理的裂缝指示曲线，WLT是对多条测井曲线（GR、SP、CAL、RLLs、RLLd、ILM、ILD、AC、CNL、DEN、RSFL）采用小波变换处理的综合裂缝指示曲线，DFA－AC是对单条测井曲线采用分形维数处理的裂缝指示曲线，DFA是对多条测井曲线采用分形维数处理的综合裂缝指示曲线，CWP是对多条测井曲线采用加权概率指数处理的综合裂缝指示曲线。可见岩心观察有裂缝的井段绝大部分在裂缝指示曲线上均有显示。对于6口井的小波变换法和分形维数法的识别结果与岩心观察结果对比数据如表2和表3所示，其 中WLT－CNL、WLT－GR、WLT－CAL、WLT－COND分别为利用中子、自然伽马、井径和感应测井曲线经小波变换处理后的裂缝识别曲线；DFA－CNL、DFA－GR、DFA－CAL、DFA－COND分别为利用中子、自然伽马、井径和感应测井曲线计算出来的分形维数裂缝识别曲线。表2为采用小波变换处理的单一曲线及综合曲线裂缝识别验证统计数据。表3为采用分形维数处理的单一曲线及综合曲线裂缝识别验证统计数据。表4为小波变换法、分形维数法和加权概率指数法裂缝识别效果验证对比数据。从表2和表3的数据可以看出，综合曲线的识别效果总比单条曲线的识别率要高。而在单条曲线的识别效果上声波时差、中子的效果较好，且通用性较强。从表4的对比数据可以看出，加权概率指数法的识别率最好，小波变换法和分形维数法二者效果相当。

图1 某井的常规测井资料3种方法裂缝识别结果

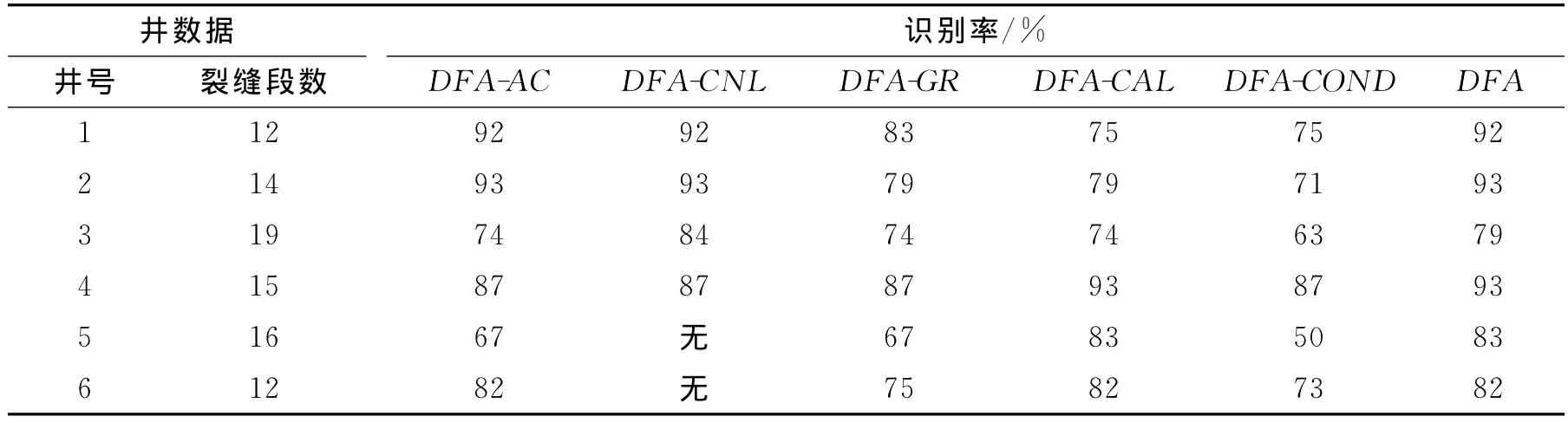
表3 分形维数识别裂缝在6口井中的验证结果

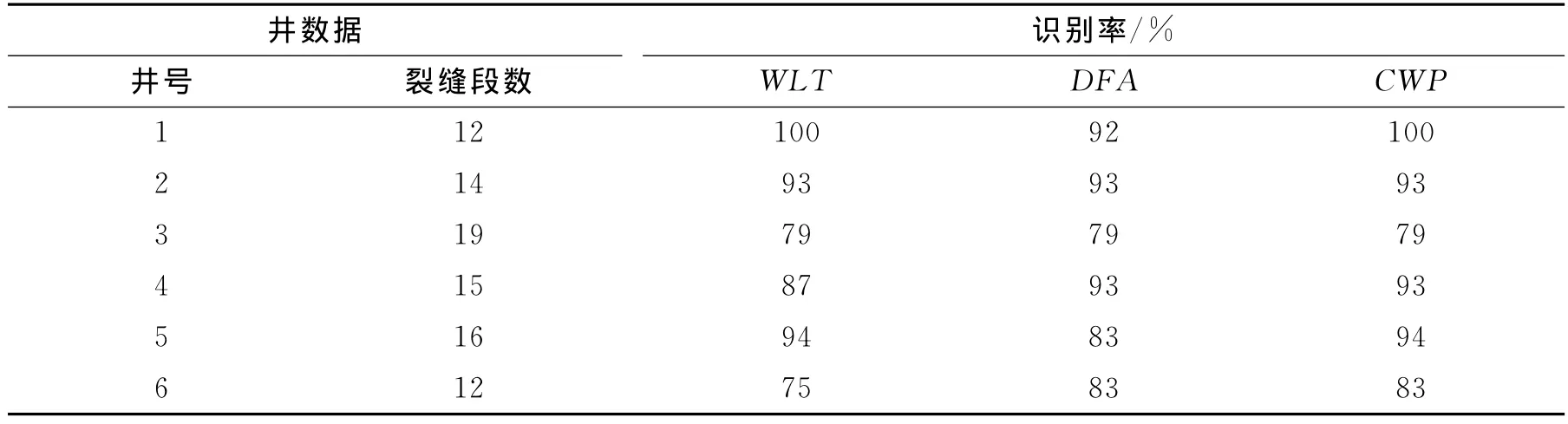
表4 3种识别裂缝方法在6口井中的识别对比

3 结 论

（1）6口取心井的常规测井资料处理验证和对比结果表明这3种方法均能识别裂缝发育层段。

（2）应用单条测井曲线识别裂缝的成功率不如采用多条曲线综合识别的概率高。

（3）不同的常规测井曲线独立识别裂缝的成功率也不相同，一般声波时差和中子测井曲线效果较好且较通用。

（4）3种方法中，加权概率指数法比其他2种方法效果好，小波变换法和分形维数法效果相似。

［1］ 陈钢花，吴文圣，王中文，等.利用地层微电阻率成像测井识别裂缝 ［J］.测井技术，1999，23（4）：279－281.

［2］ Sullivan K B，Schepel K J.Borehole Image Logs：Applications in Fractured and Thinly Bedded Reservoirs［C］∥SPWLA 36th Annual Logging Symposium，1995.

［3］ 夏宏泉，刘红歧，刘之的，等.测井曲线的分数维的计算与储层类型识别研究 ［J］.国外测井技术，2003，18（6）：9－12.

［4］ 高松洋.测井资料在裂缝识别中的应用——以H地区砂岩储层为例 ［J］.石油天然气学报，2009，31（2）：272－274.

［5］ 绪磊，齐井顺，罗明高，等.测井多参数综合识别火山岩裂缝 ［J］.天然气勘探与开发，2008，32（1）：21－25

［6］ 邓瑞，郭海敏，戴家才，等.裂缝性储层的常规测井识别方法 ［J］.勘探地球物理进展，2007，30（2）：107－110.

［7］ 邓少贵，王晓畅，范宜仁.裂缝性碳酸盐岩裂缝的双侧向测井响应特征及解释方法 ［J］.中国地质大学学报，2006，31（6）：846－850.

［8］ 文泽军.用常规测井曲线探索裂缝产状及气水划分［J］.测井技术，2005，29（5）：469－472.

［9］ 卢毓周，魏斌，李彬.常规测井资料识别裂缝性储层流体类型方法研究 ［J］.地球物理学进展，2004，19（1）：173－178.

［10］ 史謌，何涛，仵岳奇，等.用正演数值计算方法开展双侧向测井对裂缝的响应研究 ［J］.地球物理学报，2004，47（2）：359－363.

［11］ 柯式镇.裂缝地层双侧向测井响应物理模拟研究 ［J］.测井技术，2003，27（5）：353－355.

［12］ 刘兴刚，张旭.测井裂缝参数估算方法研究［J］.天然气工业，2003，23（4）：31－34.

［13］ 周灿灿，杨春顶.砂岩裂缝的成因及其常规测井资料综合识别技术研究 ［J］.石油地球物理勘探，2003，38（4）：425－430.

［14］ 金燕，张旭.测井裂缝参数估算与储层裂缝评价方法研究 ［J］.天然气工业，2002，22（增刊）：64－67.

［15］ 康义逵，金梅，文清，等.应用常规测井资料识别单井裂缝发育层段的方法 ［J］.新疆石油学院学报，2002，14（4）：29－31.

［16］ 罗利，胡培毅，周政英.碳酸盐岩裂缝测井识别方法［J］.石油学报，2001，22（3）：32－35.

［17］ 卢颖忠，黄智辉，管志宁.用常规测井资料识别裂缝发育程度的方法 ［J］.测井技术，2000，24（6）：428－432.

［18］ 孙建孟，刘蓉，梅基席，等.青海柴西地区常规测井裂缝识别方法 ［J］.测井技术，1999，23（4）：268－272.

［19］ 李善军，汪涵明，肖承文，等.碳酸盐岩地层中裂缝孔隙度的定量解释 ［J］.测井技术，1997，21（3）：205－214.

［20］ Sibbit A M，Faivre O.The Dual laterolog Response in Fracture Rock［C］∥SPWLA 26th Symposium，1985.

［21］ Daubechies I.The Wavelets Transform，Time－frequency Localization and Signal Analysis［J］.IEEE Trans.Inform.Theory，1990，36（5）：961－1005.

［22］ Sahimi M，Hashemi M.Wavelet Identification of the Spatial Distribution of Fractures［J］.Geophys.Reserv.Lett，2001，28（4）：611－614.

［23］ Behzad Tokhmchi，Hossein Memarian，Reza M Rezaee.Estimation of the Fracture Density in Fractured Zones Using Petrophysical Logs［J］.Journal of Petroleum Science and Engineering，2010（72）：206－213.