基于双闭环PI控制的电动车桥驱动控制系统建模与仿真

俞传阳，常可娟，郑 泉*，袁 剑

(1.安徽农业大学 工学院，安徽 合肥 230036；2.安徽安凯福田曙光车桥有限公司，安徽 合肥 230051； 3.合肥美桥传动系统及底盘有限责任公司，安徽 合肥 230000)

随着人类对环境和能源保护意识的增强，电动汽车需求量越来越大。电动车桥作为电动汽车的重要总成部件，直接影响着电动汽车的控制性能。目前针对电动车桥的研究主要集中在电驱动系统、驱动电机和传动部件参数匹配以及驱动控制策略的开发研究方面。文献[1]研究了电动汽车驱动电机和传动系统的参数匹配问题，得出在城市行驶的汽车车速经常处于30～50 km/h，采用固定比的传动系是可行的，可以减少车重，增加行驶里程；文献[2]研究了驱动电机与前驱动桥的耦合振动问题；文献[3]以FreescaleS12为中央芯片对电动客车驱动控制系统进行了研究与开发。

本文以电动车桥的核心驱动部件——永磁无刷直流电机(Magnet Brushless DC motor,BLDC)为研究对象，采用双闭环PI控制策略，在Matlab/Simulink中构建以BLDC为核心的驱动控制仿真系统并进行仿真研究；以STM8S105S4为中央处理器搭建硬件控制系统，并进行相关实验。

1 永磁无刷直流驱动电机的数学模型

1.1 驱动电机的端电压方程

BLDC所产生的理想反电动势为梯形波，用坐标转换的方法进行分析十分困难。在建立模型时可利用其本身的相变量构建电机数学模型，分析时可以假设驱动电机三相绕组在空间上完全对称，忽略涡流和磁滞损耗的影响，且电机的磁场不饱和；三相绕组不设有中线并采用行星连接。三相电流满足

ia+ib+ic=0，

由此可以得到简化后的BLDC三相电压平衡方程为

(1)

式中Ua、Ub、Uc为三相定子端电压，V；ea、eb、ec为三相定子实时产生的感应电动势，V；ia、ib、ic为三相定子绕组适时相电流，A；R为三相定子绕组的相等效电阻，Ω；L为三相定子的自感， H；M为三相定子绕组之间的互感，H。

1.2 驱动电机的电磁转矩方程和运动方程

BLDC的电磁扭矩由感应电动势和相电流作用产生，其电磁转矩方程可表示为

Te=(eaia+ebib+ecic)/ω，

(2)

式中ω为电机的角速度。

BLDC运行时主要考虑外部施加力矩、电机阻尼矩和转子加速阻力矩，用运动方程表示的电磁转矩为

Te=Tl+Bω+Jdω/dt，

(3)

式中Tl为负载转矩，N·m；B为阻尼系数；J为电机的转动惯量，kg·m2。

转子角度θ可以由ω经过一次积分获取。

Simulink中没有自带BLDC电机本体模块，需另行建立。BLDC的感应电动势由分段线性法[4]求出，利用S函数编写感应电动势函数和参考电流函数。图1给出了BLDC本体模块的Simulink模型。BLDC本体模块由电机、转矩和运动3部分组成，其理论公式分别见式(1)～(3)。

图1 BLDC本体模块

1.3 基于双闭环PI控制的仿真模型

仿真模型主要由转速PI控制、参考电流、PWM(Pulse Width Modulation，脉宽调制)、电压逆变器、电机本体和显示等模块组成，图2给出了转速环、电流环双闭环PI控制的Simulink模型。

图2 基于双闭环PI控制的仿真系统模型

1.4 仿真实验

仿真前相关数据设置：阻尼系数B=0.000 2 N/(m·s-1)，自感系数L=0.025 H，互感系数为0.001 H，定子相电阻为0.015 Ω，电机转动惯量为0.05 kg·m2，PI比例系数kp=10，PI积分系数ki=2.0。

仿真中电机带负载10 N·m启动，在运行0.25 s时突然加载15 N·m，仿真时间设为0.5 s，转速为900 r/min。其仿真结果见图3、4。

图3 转速响应 图4 转矩响应

由图3可以看出，电机启动后稳定转速约为893 r/min，稳态误差为0.78%，稳态响应时间为0.18 s。突然加载后，电机扭矩输出响应迅速，速度波动小，满足控制要求。

2 双闭环PI控制实例

以仿真系统模型为参考，以STM8S105S4为中央处理器设计了双闭环PI控制器，控制器的控制原理图如图5所示；控制器的硬件电路由STM8S105S4最小系统、驱动控制、转子位置检测、电流采集、电源监控、驱动电路等模块组成。

图5 控制器控制原理图

2.1 控制软件

图6 中断处理子程序流程图

软件通过程序模块化进行设计，主要包含系统数据初始化、电机调速控制、数据采集和系统保护等系统。控制系统通电后，执行初始化程序对初始状态进行设定；系统定时计算电机转速和对电机相电流信号进行A/D采样，并与给定参考转速进行比较判断，达到给定转速则保持并退出转速PI控制，否则进行转速PI调节；同时系统适时监控各部件的运行状态，一旦出现故障则触发相应的保护措施。主程序为：初始化→A/D数据采样→达到给定转速→中断处理程序。中断处理子程序如图6所示。

图7 控制器与外接设备

2.2 试验

本文借助NI数据采集设备PXI-1036对电机空载转速进行采集，试验所需设备如图7所示。

试验说明：控制器将电机的目标转速设定为900 r/min，电机空载启动；转速采集由NI数据采集设备提供，并在LabVIEW软件中以图形化界面显示，采样频率设定为10 kHz。

2.3 结果分析

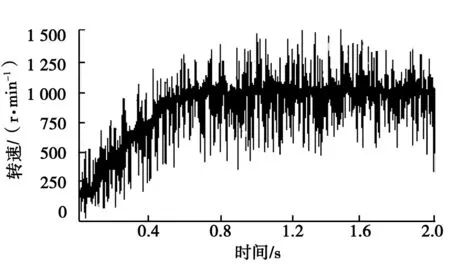
图8 转速采样波形

经过反复试验，最终设定kp=18.7，积分系数ki=1.2，此时测得电机空载转速如图8所示。由图8可以得出，电机达到900 r/min的响应时间为0.55 s左右，电机稳定转速在945 r/min左右。试验结果和仿真结果相比，电机响应时间相差较大，但稳定转速相差较小，造成这种情况的原因可能是采用的8位单片机运算能力不足以及控制程序未达最优化等。

本文提供的一种基于双闭环PI控制策略适应于电动车桥的驱动控制，为电动车桥驱动控制系统进一步开发提供一种设计思路。

参考文献：

[1]姬芬竹，高峰.电动汽车驱动电机和传动系统的参数匹配[J].华南理工大学学报：自然科学版，2004，34(4):32-37.

[2]薛玉春，张威，王连加，等.电动汽车驱动电机及前驱动桥的耦合振动研究[J].武汉理工大学学报，2010，32(15):85-89.

[3]赵轩，肖广朋，马建，等. 纯电动汽车驱动控制器研究与开发[J].科技导报.2012，30(06)：30-35.

[4]殷云华，郑宾，郑浩鑫．一种基于Matlab的无刷直流电机控制系统建模仿真方法[J]．系统仿真学报，2008，20(2)：293-298.